Đại số 10 - Bài 1: Giá trị lượng giác của góc (cung) lượng giác

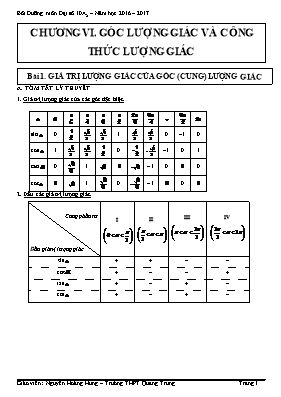
CHƯƠNG VI. GÓC LƯỢNG GIÁC VÀ CÔNG THỨC LƯỢNG GIÁC
Bài 1. GIÁ TRỊ LƯỢNG GIÁC CỦA GÓC (CUNG) LƯỢNG GIÁC
A. TÓM TẮT LÝ THUYẾT
1. Giá trị lượng giác của các góc đặc biệt.
sin
0
1
0
–1
0
cos
1
0
–1
0
1
tan
0
1
–1
0
0
cot
1
0
–1
0
2. Dấu các giá trị lượng giác.
Cung phần tư
Dấu giá trị lượng giác
I
II
III
IV
sin
+
+
–
–
cos
+
–
–
+
tan
+
–
+
–
cot
+
–
+
–
3. Hệ thức cơ bản.
DẠNG 1. THU GỌN BIỂU THỨC LƯỢNG GIÁC
B. CÁC DẠNG BÀI TẬP
A. PHƯƠNG PHÁP
Vận dụng các hệ thức lượng giác cơ bản, hằng đẳng thức đáng nhớ.
 B. BÀI TẬP MẪU
Thu gọn các biểu thức sau: 
1) . 2) .
3) . 4) 
5) 6) 
7) 8) 
9) 10) 
11) 12) 
13) 14) 
15) 16) 
17) 18) 
19) 20) 
21) 22) 
	C. BÀI TẬP TỰ LUYỆN
Thu gọn các biểu thức sau: 
a) b) .
c) d) .
e) f) .
g) h) .
k) l) .
DẠNG 2. TÍNH GIÁ TRỊ CỦA BIỂU THỨC LƯỢNG GIÁC-GIÁ TRỊ CÁC GIÁ TRỊ LƯỢNG GIÁC
A. PHƯƠNG PHÁP
Xác định dấu các giá trị lượng giác cần thiết còn lại dựa vào giá trị lượng giác của đề ra. Đôi khi có thể dùng thêm biến đổi sơ cấp để biến đổi biểu thức về dạng thu gọn hay dạng hợp lý. 
Sau đó thực hiện phép tính giá trị như trong đại số.
B. BÀI TẬP MẪU
Bài 1. Tính giá trị của biểu thức: 
a) .
b) .
Bài 2. Tính các giá trị lượng giác còn lại khi biết:
a) .
b) .
c) .
d) .
e) 
Bài 3. Tính giá trị của biểu thức sau:
a) , nếu với .
b) , biết .
c) , biết , với .
d) , biết .
e) , biết .
f) , biết .
g) , biết .
h) biết .
Bài 4. Cho . Tính
a) ; b) ; c) ; d) 
Bài 5. Cho . Tính theo m:
a) ; b) .
Bài 6. Cho . Hãy tính giá trị của biểu thức sau
1/ .	ĐS: .
2/ .	ĐS: .
3/ .	ĐS: .
Bài 7. Cho . Hãy tính theo m giá trị các biểu thức
1/ .	2/ .
3/ .	4/ .
5/ .	6/ .
Bài 8. Tính . Biết rằng
1/ .	2/ .
3/ . 	(HKII, Nguyễn Thượng Hiền – năm 2005)
4/ .	ĐS: .
5/ .	ĐS: .
Bài 9. Cho . Hãy tính
1/ .	2/ .
3/ .	4/ .
Bài 10. Tính giá trị của các biểu thức sau đây khi
1/ Cho . Tính .	ĐS: .
2/ Cho . Tính .	ĐS: .
3/ Cho . Tính.	ĐS: .
C. BÀI TẬP TỰ LUYỆN
Bài 1. Tính các giá trị lượng giác còn lại khi biết:
a) b) .
c) d) .
e) f) 
g) h) .
k) l) .
Bài 2. Tính giá trị của biểu thức sau:
a) , biết , với b) , biết .
c) , biết d) , biết .
e) , biết f) , biết .
DẠNG 3. CHỨNG MINH BIỂU THÚC LƯỢNG GIÁC ĐỘC LẬP VỚI BIẾN
A. PHƯƠNG PHÁP
Làm như dạng 1 là thu gọn biểu thức lượng giác. Nhưng kết quả rút gọn phải là một hằng số (không phụ thuộc vào biến).
Cách làm như sau khắc phục được sự phức tạp của phương pháp trên là 
Đặt 
và thực hiện thu gọn biểu thức đại số thành một hằng số (không phụ thuộc vào biến t )
C. BÀI TẬP MẪU
Bài 1. Chứng minh các biểu thức sau độc lập với biến:
1) .
2) .
3) . 
4) .
5) .
Bài 2. Chứng minh các biểu thức sau không phụ thuộc vào biến x
.
.
.
.
.
.
.
.
Bài 3. Cho . Chứng minh các đại lượng sau không phụ thuộc vào biến: 
.
Bài 4. Chứng minh các biểu thức sau độc lập với biến:
1) 
2) .
3) .
4) 
5) .
6) 
Bài 5. Cho . Chứng minh rằng biểu thức không phụ thuộc vào biến.
Bài 6. Cho . Tìm tham số m để biểu thức không phụ thuộc vào x và tính giá trị của với m vừa tìm được (nếu có).
(HKII – Chuyên Trần Đại Nghĩa – năm 1998)
Bài 7. Cho . Chứng minh rằng:
 (HKII – Chuyên Lê Hồng Phong – năm 2001)
 (HKII – Hà Nội Amsterdam – năm 2007)
C. BÀI TẬP TỰ LUYỆN
Chứng minh các biểu thức sau độc lập với biến:
a) .
b) .
c) .
d) .
e) .
f) .
g) 
DẠNG 4. CHỨNG MINH ĐẲNG THỨC LƯỢNG GIÁC
Để có thể chứng minh đẳng thức ta có thể dùng:
Chứng minh: hay 
Chứng minh: và suy ra .
Biến đổi tương đương.
A. PHƯƠNG PHÁP
B. BÀI TẬP MẪU
B. BÀI TẬP MẪU
Bài 1. Chứng minh rằng:
1) 2)
3) 4) ; 5) 6) .
7) 8) .
9) 10) .
11) 12) .
13) 14) .
15) 16) .
Bài 2. Chứng minh rằng:
1) 2) .
3) 4) .
5) 6) .
7) 8) .
9) 10) .
Bài 3. Chứng minh rằng:
1) 2) .
3) 4) .
5) 6) .
7) 8) .
9) 10) .
11) 12) .
13) 14) .
15) . 16) .
17) . 18) .
19) 20) 	
™–@&?˜—