Công thức và bài tập lượng giác 10

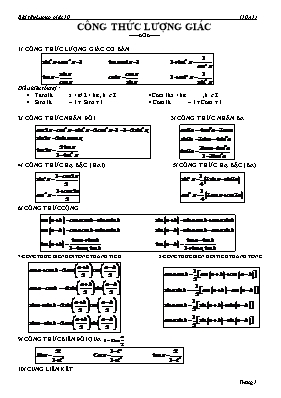
CÔNG THỨC LƯỢNG GIÁC
-----oOo-----
1/ CÔNG THỨC LƯỢNG GIÁC CƠ BẢN
Điều kiện tồn tại :
Tanx là	x ¹ p/ 2 + kp , k Î Z — Cotx là	x ¹ kp 	 , k Î Z
Sinx là	– 1 £ Sinx £ 1 — Cosx là 	– 1 £ Cosx £ 1
2/ CÔNG THỨC NHÂN ĐÔI 3/ CÔNG THỨC NHÂN BA
4/ CÔNG THỨC HẠ BẬC (HAI) 5/ CÔNG THỨC HẠ BẬC (BA)
6/ CÔNG THỨC CỘNG 
7/CÔNG THỨC BIẾN ĐỔI TỔNG THÀNH TÍCH 8/CÔNG THỨC BIẾN ĐỔI TÍCH THÀNH TỔNG
9/ CÔNG THỨC BIẾN ĐỔI QUA 
10/ CUNG LIÊN KẾT
ĐỐI (cos đối)
 ; 
BÙ (sin bù)
PHỤ (phụ chéo)
HƠN KÉM p
(tan, cot hơn kém p)
HƠN KÉM p/2
Chú ý
; 
11/ Bảng dấu
Cung
phần
tư
I
()
II
()
III
()
IV
()
cosa
+
–
–
+
sina
+
+
–
–
tana
+
–
+
–
cota
+
–
+
–
12/ Hằng đẳng thức 
 Từ đó ta suy ra: — a2 + b2 = ( a + b)2 – 2ab — a3 + b3 = ( a + b)3 – 3ab( a + b)
BÀI TẬP CHƯƠNG 6
Bài : GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT CUNG
* Dạng 1: Tính giá trị lượng giác của một cung
 Phương pháp: sử dụng Công thức lượng giác cơ bản và bảng dấu
Bài tập áp dụng:
1/ Cho và . Tính .
2/ Cho sinx = và < x < p. Tính cosx, tanx, cotx.
3/ Cho và .Tính .
4/ . Tính .
5/ Cho và . Tính .
6/ Cho và .Tính .
7/ Cho Tính .
8/ Tính các giá trị lượng giác còn lại, biết:
 	 a) sinx = và < x < p	 b) cosx = và 
* Dạng 2: Chứng minh biểu thức
 Phương pháp: sử dụng công thức lượng giác cơ bản và những công thức suy ra được từ đó
Bài tập áp dụng:
1/ Chứng minh các biểu thức sau
a) ; b) ; c) 
d) ; e) ; f) ;
g) ; h) ; i) 
2/ Chứng minh các biểu thức sau
 a) ; b) 
 c) ; d) ; e) 
 f); g) ; h) 
* Dạng 3: Tính giá trị biểu thức
Phương pháp: biến đổi biểu thức cần tính về dạng có chứa biểu thức mà đề đã cho biết giá trị, sau đó thay giá trị đã vào biểu thức đã được biến đổi
Bài tập áp dụng:
1/ Cho tanx = 3/5 . Tính giá trị các biểu thức sau : A = ; B = 	
 2/ Cho cotx = -2 . Tính giá trị các biểu thức sau : 
 M = ; N = ; P = 
 3/ Cho . Tính: 
* Dạng 4: Rút gọn biểu thức
 Phương pháp: sử dụng Công thức lượng giác cơ bản và cung liên kết
Rút gọn các biểu thức sau:
1/ 2/ 
3/ 4/ 
5/ ; 6/ 
* Dạng 4: Biểu thức lượng giác độc lập đối với biến
Phương pháp: sử dụng các công thức đã học biến đổi biểu thức đã cho để được kết quả là một hằng số.
Bài tập áp dụng:
Chứng minh các biểu thức sau không phụ thuộc vào x
1/ 2/ B = 2(cos6x + sin6x) – 3(cos4x + sin4x)	 	 
3/ C = - (1 + tan2x)2 4/ D = + sinx.cosx
Bài : CÔNG THỨC LƯỢNG GIÁC
* Dạng 1: Tính giá trị lượng giác của một cung
 Phương pháp: sử dụng kết hợp: Công thức lượng giác cơ bản, Bảng dấu, Các công thức lượng giác đã học
Bài tập áp dụng:
1/ Cho sinx = - 0,96 với 
a/ Tính cosx, tanx, cotx b/ Tính , sin2x, cos2x
2/ Biết . Tính 
3/ Cho . Tính sin2x, cos2x, tan2x 
4/ Cho . Tính: 
 a) b) 
5) Biết . Tính cos(a+b), sin(a-b).
6) Cho tanx = -1 và . Tính:
 a) b) 
7) Cho và .Tính:
 a) b) 
* Dạng 2: Chứng minh biểu thức
 Phương pháp: sử dụng công thức lượng giác cơ bản, công thức cộng, công thức nhân đôi, công thức hạ bậc, công thức biến đổi tổng thành tích, tích thành tổng.
Bài tập áp dụng: 
1/ Chứng minh:
a) ; b) 
c) d) 
e) ; f) ; g) ; h) 
i) ; j) 
2/ Chứng minh
a) ; b) 
c) ; d) 
e) sin2a.tana + cos2a.cota + 2sina.cosa = tana + cota; f) tana.tanb =	 
g) ; h) cot2a.cot2b – = 1	
i) ; j) 
* Dạng 3: Rút gọn biểu thức
Rút gọn các biểu thức sau
a) ; b) ; c) 
d) ; e) 
f) 
* Dạng 4: Biểu thức lượng giác độc lập đối với biến
Chứng minh các biểu thức sau không phụ thuộc vào x
* Dạng 6: Tính giá trị biểu thức
Bài tập áp dụng:
1/ Biết .Tính giá trị biểu thức
2/ Cho . Tính B = cos4a
3/ Biết .Tính giá trị biểu thức 
4/ Biết cosx = 3/4. Tính giá trị các biểu thức sau:
a) b) 
c) 
5/ Biết .Tính