Công thức Hình học

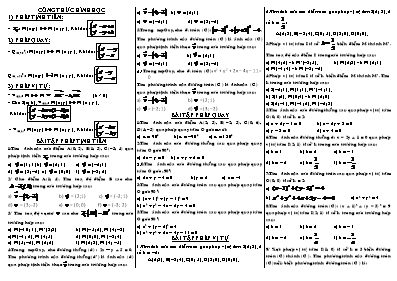
CƠNG THỨC HÌNH HỌC
1) PHÉP TỊNH TIẾN:
· : M(x; y) M¢(x¢; y¢). Khi đó: 
2) PHÉP QUAY:
· Q(O,900): M(x; y) M¢(x¢; y¢). Khi đó: 
Q(O,–900): M(x; y) M¢(x¢; y¢). Khi đó: 
3) PHÉP VỊ TỰ:
· V(I,k): M M¢ Û 	(k ¹ 0)
· Cho I(a; b). V(I,k): M(x; y) M¢(x¢; y¢).
 Khi đó: 
 · V(O,k): M(x; y) M¢(x¢; y¢). Khi đó: 
BÀI TẬP PHÉP TỊNH TIẾN
1/Tìm ảnh của các điểm A(0; 2), B(1; 3), C(–3; 4) qua phép tịnh tiến trong các trường hợp sau:
a) = (1; 1) b) = (2; 1)	c) = (–2; 1)	
d) = (3; –2)	e) = (0; 0)	f) = (–3; 2)	
2/ Cho điểm A(1; 4). Tìm toạ độ điểm B sao cho trong các trường hợp sau:
a) 	b) = (2; 1)	 c) = (–2; 1)
d) = (3; –2)	 e) = (0; 0)	 f) = (–3; 2)
3/ Tìm toạ độ vectơ sao cho trong các trường hợp sau:
a) M(-10; 1), M’(3; 8)	b) M(-5; 2), M¢(4; -3)	
c)M(–1; 2), M¢(4; 5)	d) M(0; 0), M¢(–3; 4)	
c) M(5; –2), M¢(2; 6)	f) M(2; 3), M¢(4; –5)
4/Trong mpOxy, cho đường thẳng (d) : 2x - y + 5 = 0. Tìm phương trình của đường thẳng (d’) là ảnh của (d) qua phép tịnh tiến theo trong các trường hợp sau:
a) 	b) = (2; 1)	
c) = (–2; 1)	d) = (3; –2)
5/Trong mpOxy, cho đ. tròn (C):. Tìm phương trình của đường tròn (C¢) là ảnh của (C) qua phép tịnh tiến theo trong các trường hợp sau:
a) 	 b) = (2; 1)	
c) = (–2; 1)	d) = (3; –2)
6/ Trong mpOxy, cho đ. tròn (C): x2 + y2 + 2x – 4y – 11 = 0
Tìm phương trình của đường tròn (C¢) là ảnh của (C) qua phép tịnh tiến theo trong các trường hợp sau:
a) 	b) = (2; 1)	
c) = (–2; 1)	d) = (3; –2)
BÀI TẬP PHÉP QUAY
1/Tìm ảnh của các điểm A(2; 3), B(–2; 3), C(0; 6), D(4;–3) qua phép quay tâm O góc a với:
a) a = 900	 b) a = –900	 c) a = 1800
2/Tìm ảnh của các đường thẳng sau qua phép quay tâm O góc 900:
a) 2x – y = 0	b) x + y + 2 = 0	
3/2/Tìm ảnh của các đường thẳng sau qua phép quay tâm O góc -900:
a) 2x + y – 4 = 0	 b) y = 2 	c) x = –1
3/Tìm ảnh của các đường tròn sau qua phép quay tâm O góc 900:
a) (x + 1)2 + (y – 1)2 = 9	
b) x2 + y2 – 4x – 2y – 4 = 0
3/Tìm ảnh của các đường tròn sau qua phép quay tâm O góc 900:
a) x2 + (y – 2)2 = 4
b) x2 + y2 + 2x – 4y – 11 = 0
BÀI TẬP PHÉP VỊ TỰ
1/Tìm ảnh của các điểm sau qua phép vị tự tâm I(2; 3), tỉ số k = –2: 
 A(2; 3), B(–3; 4), C(0; 5), D(3; 0), O(0; 0).
2/Tìm ảnh của các điểm sau qua phép vị tự tâm I(2; 3), tỉ số k = : 
 A(2; 3), B(–3; 4), C(0; 5), D(3; 0), O(0; 0).
3/Phép vi tự tâm I tỉ số biến điểm M thành M’. Tìm toạ độ của điểm I trong các trường hợp sau:
a) M(4; 6) và M’(–3; 5). 	b) M(2; 3) và M¢(6; 1)	
c) M(–1; 4) và M¢(–3; –6)
4/Phép vị tự tâm I tỉ số k biến điểm M thành M’. Tìm k trong các trường hợp sau:
a) I(–2; 1), M(1; 1), M’(–1; 1).	
b) I(1; 2), M(0; 4) và M¢(2; 0)	
c) I(2; –1), M(–1; 2), M¢(–2; 3)
5/Tìm ảnh của các đường thẳng sau qua phép vị tự tâm O(0; 0) tỉ số k = 2:
a) x + 2y – 1 = 0	b) x – 2y + 3 = 0	
c) y – 3 = 0	d) x + 4 = 0
6/Tìm ảnh của đường thẳng d: x – 2y + 1 = 0 qua phép vị tự tâm I(2; 1) tỉ số k trong các trường hợp sau: 
a) k = 1	b) k = 2	c) k = – 1	
d) k = – 2	e) k = 	f) k = 
7/Tìm ảnh của các đường tròn sau qua phép vị tự tâm O(0; 0) tỉ số k = 2:
a) 	
b) 	c) x2 + y2 = 4	
8/Tìm ảnh của đường tròn (C): (x + 1)2 + (y – 3)2 = 9 qua phép vị tự tâm I(2; 1) tỉ số k trong các trường hợp sau: 
a) k = 1	b) k = 2	c) k = – 1	
d) k = – 2	e) k = 	f) k = 
9/ Xét phép vị tự tâm I(1; 0) tỉ số k = 3 biến đường tròn (C) thành (C¢). Tìm phương trình của đường tròn (C) nếu biết phương trình đường tròn (C¢) là:
a) 	
b) 	c) 
Chương II: ĐƯƠNG THẲNG VÀ MẶT PHẲNG TRONG KHƠNG GIAN- QUAN HỆ SONG SONG
1. Xác định một mặt phẳng 
· Ba điểm không thẳng hàng thuộc mặt phẳng. (mp(ABC), (ABC))
· Một điểm và một đường thẳng không đi qua điểm đó thuộc mặt phẳng. (mp(A,d))
· Hai đường thẳng cắt nhau thuộc mặt phẳng. (mp(a, b))
2. Một số qui tắc vẽ hình biểu diễn của hình không gian
· Hình biểu diễn của đường thẳng là đường thẳng, của đoạn thẳng là đoạn thẳng.
· Hình biểu diễn của hai đường thẳng song song là hai đường thẳng song song, của hai đường thẳng cắt nhau là hai đường thẳng cắt nhau.
· Hình biểu diễn phải giữ nguyên quan hệ thuộc giữa điểm và đường thẳng.
· Đường nhìn thấy vẽ nét liền, đường bị che khuất vẽ nét đứt.
VẤN ĐỀ 1: Tìm giao tuyến của hai mặt phẳng 
	Muốn tìm giao tuyến của hai mặt phẳng ta có thể tìm hai điểm chung phân biệt của hai mặt phẳng. Khi đó giao tuyến là đường thẳng đi qua hai điểm chung đó.
1/ Cho hình chóp S.ABCD. Đáy ABCD có AB cắt CD tại E, AC cắt BD tại F.
	a) Tìm giao tuyến của các cặp mặt phẳng (SAB) và (SCD), (SAC) và (SBD).
	b) Tìm giao tuyến của (SEF) với các mặt phẳng (SAD), (SBC).
2/ Cho hình chóp S.ABCD, có đáy ABCD là hình bình hành tâm O. M, N, P lần lượt là trung điểm của BC, CD, SO. Tìm giao tuyến của mp(MNP) với các mặt phẳng (SAB), (SAD), (SBC) và (SCD).
3/ Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của AC và BC. K là một điểm trên cạnh BD sao cho KD < KB. Tìm giao tuyến của mp(IJK) với (ACD) và (ABD).
4/ Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của AD và BC.
	a) Tìm giao tuyến của 2 mặt phẳng (IBC) và (JAD).
	b) M là một điểm trên cạnh AB, N là một điểm trên cạnh AC. Tìm giao tuyến của 2 mặt phẳng (IBC) và (DMN).
5/ Cho tứ diện (ABCD). M là một điểm bên trong DABD, N là một điểm bên trong DACD. Tìm giao tuyến của các cặp mặt phẳng (AMN) và (BCD), (DMN) và (ABC).
VẤN ĐỀ 2: Tìm giao điểm của đường thẳng và mặt phẳng 
Muốn tìm giao điểm của một đường thẳng và một mặt phẳng ta có thể tìm giao điểm của đường thẳng đó với một đường thẳng nằm trong mặt phẳng đã cho.
Cho tứ diện ABCD. Trên AC và AD lần lượt lấy các điểm M, N sao cho MN không song song vói CD. Gọi O là một điểm bên trong DBCD.
a) Tìm giao tuyến của (OMN) và (BCD).
b) Tìm giao điểm của BC và BD với mặt phẳng (OMN).
Cho hình chóp S.ABCD. M là một điểm trên cạnh SC.
a) Tìm giao điểm của AM và (SBD).
b) Gọi N là một điểm trên cạnh BC. Tìm giao điểm của SD và (AMN).
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC và BC. K là một điểm trên cạnh BD và không trùng với trung điểm của BD. Tìm giao điểm của CD và AD với mặt phẳng (MNK).
Cho tứ diện ABCD. M, N là hai điểm lần lượt trên AC và AD. O là một điểm bên trong DBCD. Tìm giao điểm của: 
a) MN và (ABO).	b) AO và (BMN).
HD:	a) Tìm giao tuyến của (ABO) và (ACD).
	b) Tìm giao tuyến của (BMN) và (ABO).
Cho hình chóp S.ABCD, có đáy là hình thang, cạnh đáy lớn AB. Gọi I, J, K là ba điểm lần lượt trên SA, AB, BC.
a) Tìm giao điểm của IK với (SBD).
b) Tìm các giao điểm của mặt phẳng (IJK) với SD và SC.
HD:	a) Tìm giao tuyến của (SBD) với (IJK).
	b) Tìm giao tuyến của (IJK) với (SBD và (SCD).
HAI ĐƯỜNG THẲNG SONG SONG
1. Định nghĩa	
2. Tính chất
· Nếu ba mặt phẳng phân biệt cắt nhau từng đôi một theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng qui hoặc đôi một song song.
· Nếu hai mặt phẳng cắt nhau lần lượt đi qua hai đường thẳng song song thì giao tuyến của chúng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
· Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.