Chuyên mục học giải toán trắc nghiệm 12 - Bài viết số 4: Một số bài tập trắc nghiệm hình học liên hệ thực tế

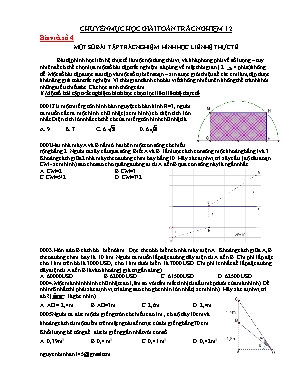
CHUYÊN MỤC HỌC GIẢI TOÁN TRẮC NGHIỆM 12
Bài viết số 4 
MỘT SỐ BÀI TẬP TRẮC NGHIỆM HÌNH HỌC LIÊN HỆ THỰC TẾ .
Bài tập hình học liên hệ thực tế là một nội dung thú vị và khá phong phú về số lượng – tuy nhiên để có thể chọn lựa một số bài tập trắc nghiệm đáp ứng về mặt thời gian ( 2 4 phút) không dễ. Một số bài tập được sưu tập và một số tự biên soạn – xin được giới thiệu để các em làm, tập dượt khả năng giải toán trắc nghiệm. Vì thời gian dành cho bài viết không nhiều nên không thể tránh khỏi những điều thiếu sót. Các học sinh thông cảm.
I/ Một số bài tập trắc nghiệm hình học chọn lọc liên liên hệ thực tế 
0001.Từ một miếng tôn hình bán nguyệt có bán kính R=3, người ta muốn cắt ra một hình chữ nhật (xem hình) có diện tích lớn nhất. Diện tích lớn nhất có thể có của miếng tôn hình chữ nhật là
A. 9.	 B. 7.	 C. 6.	 D. 6.
0002.Hai nhà máy A và B nằm ở hai bên một con sông có chiều rộng bằng 2. Người ta xây cầu qua sông. Biết A và B lần lượt cách con sông một khoảng bằng1 và 3. Khoảng cách giữa 2 nhà máy theo đường chim bay bằng 10. Hãy xác định vị trí xây cầu (độ dài đoạn CM - xem hình) sao cho sao cho quãng đường đi từ A đến B qua con sông này là ngắn nhất.
A. CM=2.	 B. CM=3.	
C. CM=5/2.	 D. CM=7/2.
0003. Hòn đảo B cách bờ biển 6km . Dọc theo bờ biển có nhà máy điện A. Khoảng cách giữa A,B theo đường chim bay là 10 km. Người ta muốn lắp đặt đường dây điện từ A đến B. Chi phí lắp đặt cho 1 km trên bờ là 3000 USD, cho 1 km dưới biển là 7000 USD. Chi phí ít nhất để lắp đặt đường dây điện từ A đến B là vào khoảng ( giá trị gần đúng) 
A. 60000 USD	B. 62000 USD	C. 61500 USD	D. 62500 USD
0004. Một màn hình hình chữ nhật cao 1,8m so với tầm mắt tính (từ đầu mép dưới của màn hình). Để nhìn rõ nhất thì phải xác định vị trí đứng sao cho góc nhìn lớn nhất ( xem hình). Hãy xác định vị trí đó ?( là góc nhìn)
A. AO = 2,4 m	B. AO=3m 	C. 2,6m	D. 2,4m
0005.Người ta đúc một bi giếng tròn có chiều cao 1m , có độ dày 10cm và khoảng cách từ một điểm trên mặt ngoài đến trục của bi giếng bằng 70 cm . Khối lượng bê tông để đúc bi giếng gần nhất với con số 
A. 0,39 m3	B. 0,4 m3	C. 0,41 m3	D. 0,42 m3
0006.Đường gấp khúc ABCD có độ dài bằng 12 và ABCD là hình chữ nhật. Thể tích lớn nhất của khối tròn xoay có được khi ta quay hình chữ nhật ABCD quanh đường thẳng AD là
A. 	B. 9p 	C. 	D.
0007.Người ta cắt một hình quạt có góc a ở tâm bằng bao nhiêu từ một miếng tôn hình tròn để cuộn lại thành một hình nón có góc ở đỉnh bằng arccos. Giá tri a bằng 
A. 	B. 	C. 	D. 
0008. Một hình nón đỉnh S có bán kính đáy bằng và đường sinh bằng 2. Thiết diện qua trục hình nón là DSAB. M là trung điểm trên SA. Quãng đường đi ngắn nhất trên bề mặt hình nón từ M đến B là
A. 	B. 	C. 2	D. 
0009.Thể tích lớn nhất của khối tròn xoay có được khi ta quay hình tam giác có độ dài 3 cạnh là 3,4,5 quanh đường thẳng chứa một cạnh của nó là
A. 18 	B. 12	C. 20	D. 16
0010. Cho tam giác cân có góc ở đỉnh là 1200 và độ dài cạnh bên bằng 3 . Thể tích khối tròn xoay có được khi ta quay tam giác cân quanh đường thẳng chứa cạnh bên là 
A. 	B.	C. 	D. 
0011. Nếu trải 2 mặt ABD và BCD của tứ diện ABCD lên một mặt phẳng ta được hình chữ nhật ABCD có kích thước 3 x 4. Một tứ diện như thế, có thể tích lớn nhất bằng
A. 	B. 	C. 	D. 
0012. Một cái phểu hình nón có chiều cao bằng 70 cm , bán kính đáy bằng 10 cm . Khoảng cách từ đỉnh phểu đến tâm mặt thoáng bằng 30 cm . Ngưởi ta bỏ vào phểu một vật thể rắn chìm hoàn toàn trong nước và lúc này nước trong phểu dâng lên 20 cm. Thể tích vật thể rắn là 
A. 8370 cm3	B. 8380 cm3	
C. 8360 cm3	D. 8390 cm3
II/ Hướng dẫn giải các bài tập trong mục I
0001. Gọi chiều rộng hình chữ nhật là x . Chiều dài hình chữ nhật là 
Diện tích hình chữ nhật là S= x. 
Dấu = xảy ra  MaxS=9. Chọn A
0002. Quãng đường đi từ A đến B qua con sông này ngắn nhất khi tổng AM+BN nhỏ nhất. 
Bỏ qua chiều rộng con sông, khi hai bờ sông nhập một (xem hình 2) ta có CD=8. 
Điểm M cần tìm là giao điểm của AB và CD .Ta có: 
0003. Xem hình. Đặt CM=x.( 0£ x £ 8) khi đó AM =8-x
BM= . Gọi S là chi phí lắp đặt đường dây từ A đến B. Ta có:
S= 3000. (8-x) + 7000
= 1000( 24-3x+7) 
S’= 1000(-3+7)=0 Þ 7x=3
Þ 40x2 = 9.36 Þ x=.
S(0) = 66000 ÚD, S( 8)= 70000USD, S() 
MinS - Chọn B
0004. Đặt x=AO. Ta có: tan a = tan(( a+ b) – b ) = 
a lớn nhất Ûtan a lớn nhất Û x=2,4 . Chọn D
0005. Ta có: R =70 cm, r=60 cm , h=1m
Thể tích (Khối lượng bê tông) bi giếng là V= VR-Vr = ph(R2-r2) = p.( 0,49-0,36)=0,13. p »0,41 (m3)
Chọn C
0006.Khối tròn xoay có được khi ta quay hình chữ nhật ABCD quanh đường thẳng AD là khối trụ có chiều cao h, bán kính đáy r .Thể tích khối trụ là V= pr2h
Ta có AB+BC+CD =12 Þ 2r+h=12
V= pr2h £ . Dấu bằng xảy ra khi r=h=4
MaxV= . Chọn C
0007.Giả sử miếng tôn có bán kính R. Hình nón có bán kính đáy r và độ dài đường sinh l=R.
Thiết diện qua trục là tam giác SAB có SA=SB=l(=R) có góc ở đỉnh S bằng arccos. 
Ta có: AB2= SA2+ SB2- 2SA.SB cosS = 2R2(1-cosS)= 2R2(1- )= Þ 4r2= Þ r =
Tính diện tích xung quanh hình nón theo hai cách:
Sxq = p rl = p rR ; Sxq= Shquat = Þ p rR= Þ Þ a =
0008.
Cắt mặt xung quanh của hình nón theo 2 đường sinh SA,SB ta được 2 nửa hình nón ( không đáy). Trải một nửa hình nón ta được một hình quạt SAB có tâm S, bán kính R = 2 . Gọi a là góc ở tâm . Diện tích hình quạt SAB bằng một nửa diện tích xung quanh hình nón và bằng . Mặt khác diện tích hình quạt SAB bằng Þ 
Trong tam giác SBM vuông tại S ta có: BM = 
0009.Thể tích lớn nhất của khối tròn xoay có được khi ta quay hình tam giác quanh đường thẳng chứa cạnh có độ dài bằng 3. Max V =16.
0010. Thể tích lớn nhất của khối tròn xoay cần tìm là V . V= V1-V2
V1 là thể tích khối nón sinh ra bởi việc quay D ACD quanh AB
V2 là thể tích khối nón sinh ra bởi việc quay D BCD quanh AB
Chọn A
0011.Tứ diện có thể tích lớn nhất khi 2 mặt ABD, BCD nằm trên 2 mặt phẳng vuông góc . trong trường hợp này thể tích tứ diện ABCD bằng 
0012. 
Mặt thoáng lúc chưa bỏ vật thể có bán kính r1 mà
Mặt thoáng lúc bỏ vật thể có bán kính r2 mà
 ( r là bán kính đáy của phểu)
Thể tích vật thể là bằng 
 ----------------------------
Hẹn gặp lại các em trong bài viết số 5:
MỘT SỐ BÀI TẬP TRẮC NGHIỆM GIẢI TÍCH VỀ PHẦN HÀM SỐ MŨ, HÀM SỐ LOGARIT .