Chuyên đề: Phương pháp toạ độ trong không gian - Đề 07

GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM
CHUYÊN ĐỀ : PHƯƠNG PHÁP TOẠ ĐỘ TRONG KHÔNG GIAN 
ĐỀ 007
C©u 1 : 
Mặt phẳng nào sau đây chứa trục Oy?
A.
–y + z = 0
B.
-2x + z =0
C.
-2x – y + z =0
D.
-2x – y = 0
C©u 2 : 
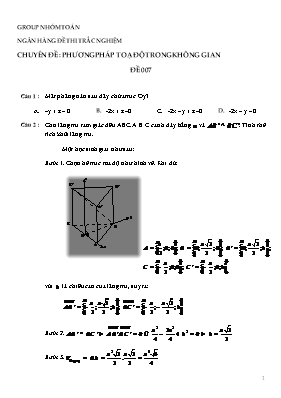
Cho lăng trụ tam giác đều ABC.A’B’C’ cạnh đáy 
bằng và . Tính thể tích khối lăng trụ.
	Một học sinh giải như sau:
Bước 1: Chọn hệ trục toạ độ như hình vẽ. Khi đó:
với là chiều cao của lăng trụ, suy ra:
Bước 2: 
Bước 3: 
Bài giải này đã đúng chưa? Nếu sai thì sai ở bước nào?
A.
Sai ở bước 2
B.
Sai ở bước 1
C.
Sai ở bước 3
D.
Đúng
C©u 3 : 
Trong không gian Oxyz cho mặt cầu , và mặt phẳng . Khoảng cách từ tâm I của mặt cầu (S) đến mặt phẳng (P) là 
A.
2
B.
1
C.
3
D.
4
C©u 4 : 
Trong không gian tọa độ Oxyz, cho điểm M=(3; 1; 2). Phương trình của mặt phẳng đi qua hình chiếu của M trên các trục tọa độ là:
A.
-3x – y – 2z =0
B.
2x + 6y + 3z – 6 =0
C.
3x + y + 2z = 0
D.
-2x – 6y – 3z – 6 =0
C©u 5 : 
Trong không gian Oxyz cho ba vectơ . Trong các mệnh đề sau, mệnh đề nào sai?
A.
B.
C.
D.
C©u 6 : 
Trong không gian (Oxyz). Cho đường thẳng . và mặt phẳng (P):. Mặt phẳng (Q) chứa và vuông góc với (P) có phương trình là:
A.
B.
C.
D.
C©u 7 : 
Trong không gian (Oxyz). Cho điểm và đường thẳng . Tọa độ hình chiếu vuông góc của M lên là:
A.
B.
C.
D.
C©u 8 : 
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng và đường thẳng . Trong các mệnh đề sau, mệnh đề nào đúng.
A.
B.
 cắt 
C.
D.
C©u 9 : 
Trong không gian Oxyz cho hai điểm và mặt phẳng (P): . Gọi là điểm trên (P) sao cho MA+MB nhỏ nhất. Giá trị của là
A.
1
B.
3
C.
2
D.
4
C©u 10 : 
Trong không gian với hệ tọa độ Oxyz, cho điểm và hai đường thẳng và . Mệnh đề nào dưới đây là đúng.
A.
, và M đồng phẳng
B.
 nhưng 
C.
 nhưng 
D.
 và vuông góc nhau
C©u 11 : 
Cho hai đường thẳng và . 
Phương trình đường vuông góc chung của và là:
A.
B.
C.
D.
C©u 12 : 
Trong không gian với hệ tọa độ cho 3 điểm , , . Với giá trị nào của thì tam giác vuông tại ?
A.
B.
C.
D.
C©u 13 : 
Trong không gian (Oxyz).Cho 3 điểm . Điểm M thuộc đường thẳng AB mà có tọa độ là:
A.
B.
C.
D.
C©u 14 : 
Trong không gian với hệ tọa độ Oxyz, cho bốn điểm .Tứ giác là hình gì?
A.
Hình thang
B.
Hình bình hành
C.
Hình thoi
D.
Hình vuông
C©u 15 : 
Trong không gian với hệ tọa độ Oxyz, cho ba mặt phẳng 
Để có chung giao tuyến thì tổng là
A.
-4
B.
8
C.
-8
D.
4
C©u 16 : 
Cho 4 điểm , , , . Bộ 3 điểm nào sau đây là thẳng hàng:
A.
B.
C.
D.
C©u 17 : 
Cho các điểm A(1; -2; 1), B(2; 1; 3) và mặt phẳng (P) : x – y + 2z – 3 = 0. Đường thẳng AB cắt mặt phẳng (P) tại điểm có tọa độ:
A.
B.
C.
D.
C©u 18 : 
Mặt phẳng (Q) đi qua hai điêm A(1; 0; 1), B(2; 1; 2) và vuông góc với mặt phẳng cắt trục oz tại điểm có cao độ	
A.
2
B.
4
C.
3
D.
1
C©u 19 : 
Cho hai điểm và mp(P): . Đường thẳng nằm trên mp(P) sao cho mọi điểm của cách đều hai điểm A, B có phương trình là:
A.
B.
C.
D.
C©u 20 : 
Góc giữa hai đường thẳng d : và d’ :
 là :
A.
B.
C.
D.
C©u 21 : 
Cho hai đường thẳng d1: = = , d2: = = . Hai đường thẳng đó:
A.
Chéo nhau
B.
Trùng nhau
C.
Cắt nhau
D.
Song song
C©u 22 : 
Cho ba điểm A(1; 0; 1), B(-1; 1; 0), C(2; -1; -2). Phương trình mặt phẳng (ABC) là: 
A.
x – 2y + 3z – 6 = 0
B.
- 4x – 7y + z – 2 = 0
C.
x – 2y + 3z + 1 = 0
D.
4x + 7y – z – 3 = 0.
C©u 23 : 
Cho đường thẳng và mp(P): . Mặt phẳng chứa và vuông góc với mp(P) có phương trình là:
A.
B.
C.
D.
C©u 24 : 
Cho hai mặt phẳng . Điểm nằm trên cách điều và là:
A.
B.
C.
D.
C©u 25 : 
Cho hai đường thẳng và .
Mặt phẳng cách đều hai đường thẳng và có phương trình là:
A.
B.
C.
D.
C©u 26 : 
Trong không gian toạ độ Oxyz, cho hai điểm A(1; -1; 0) và B(-2; 0; 1). Phương trình mặt phẳng trung trực (P) của đoạn thẳng AB là:
A.
-3x + y + z +3 =0
B.
-6x + 2y + 2z – 3=0
C.
-6x + 2y + 2z + 3=0
D.
-3x + y + z -3 =0
C©u 27 : 
Cho hai véctơ khác . Phát biểu nào sau đây không đúng?
A.
 có độ dài là 
B.
 khi hai véctơ cùng phương.
C.
 vuông góc với hai véctơ 
D.
 là một véctơ
C©u 28 : 
Trong không gian (Oxyz). Cho điểm và mặt phẳng 
(P): . Mặt cầu (S) tâm A tiếp xúc với mặt phẳng (P) tại điểm H có tọa độ là:
A.
B.
C.
D.
C©u 29 : 
Cho , , và . Mệnh đề nào sau đây là đúng
A.
 tạo thành tứ diện
B.
Diện tích bằng diện tích 
C.
 là hình chóp đều
D.
 là hình vuông
C©u 30 : 
Trong không gian Oxyz cho mặt cầu . Phương trình nào sau đây là phương trình của mặt phẳng tiếp xúc với mặt cầu (S) ?
A.
B.
C.
D.
C©u 31 : 
Cho mặt phẳng (P) : 2x + y - 2z - 1 = 0 và đường thẳng d : . Phương trình mặt phẳng chứa d và vuông góc với (P) là : 
A.
x + 8y + 5z + 31 = 0
B.
5x + y + 8z + 14 = 0
C.
5x + y + 8z = 0
D.
x + 8y + 5z +13 = 0
C©u 32 : 
Mặt phẳng nào sau đây cắt các trục tọa độ Ox, Oy, Oz lần lượt tại A, B, C sao cho tam giác ABC nhận điểm G(1; 2; 1) làm trọng tâm?
A.
x + 2y + 2z -6 =0
B.
2x + y + 2z – 6 =0
C.
2x + 2y + z – 6=0
D.
2x + 2y + 6z – 6 =0
C©u 33 : 
Trong không gian (Oxyz). Cho mặt cầu
 (S) :. Điểm A thuộc mặt cầu (S) và có tọa độ thứ nhất bằng -1. Mặt phẳng (P) tiếp xúc với (S) tại A có phương trình là:
A.
B.
C.
D.
C©u 34 : 
Trong không gian với hệ tọa độ 0xyz, cho M(-2;1;0) và đường thẳng . Điểm N thuộc sao cho . Tọa độ điểm N là:
A.
B.
C.
D.
C©u 35 : 
Trong không gian với hệ toạ độ Oxyz, cho . Mặt phẳng (P) thay đổi qua A,B cắt các trục Ox, Oy lần lượt tại B(0; b; 0), C(0; 0; c) (b > 0, c > 0). Hệ thức nào dưới đây là đúng.
A.
B.
C.
D.
C©u 36 : 
Mặt cầu tâm I(1; -2; 3) tiếp xúc với mặt phẳng (P) : 2x – y + 2z – 1 = 0 có phương trình :
A.
B.
C.
D.
C©u 37 : 
Trong không gian với hệ toạ độ Oxyz, cho đường thẳng và mặt phẳng .Đường thẳng D qua song song với mặt phẳng và vuông góc với đường thẳng d. Véctơ chỉ phương của D là:
A.
B.
C.
D.
C©u 38 : 
Cho mặt phẳng (P) : 2x – 2y – z – 4 = 0 và mặt cầu (S) : . Bán kính đường tròn giao tuyến là:
A.
2
B.
5
C.
3
D.
4
C©u 39 : 
Nếu mặt phẳng qua ba điểm M(0; -1; 1), N(1; -1; 0), và P(1; 0; -2) thì nó có một vectơ pháp tuyến là:
A.
B.
C.
D.
C©u 40 : 
Cho hai điểm và đường thẳng . Điểm mà nhỏ nhất có toạ độ là:
A.
B.
C.
D.
C©u 41 : 
 Trong không gian (Oxyz). Cho mặt cầu 
(S): và mặt phẳng 
(P): ( m là tham số). Mặt phẳng (P) tiếp xúc với mặt cầu (S) ứng với giá trị m là:
A.
B.
C.
D.
C©u 42 : 
Trong không gian (Oxyz). Cho tứ diện ABCD biết . Chiều cao của tứ diện hạ từ đỉnh A là:
A.
B.
C.
D.
C©u 43 : 
Trong không gian với hệ tọa độ Oxyz, gọi là góc hợp bởi đường thẳng và mặt phẳng thì bằng:
A.
B.
C.
D.
C©u 44 : 
Cho hai đường thẳng và . Khoảng cách giữa và bằng:
A.
B.
C.
D.
C©u 45 : 
Hai mặt phẳng : 3x + 2y – z + 1 = 0 và : 3x + y + 11z – 1 = 0
A.
Song song với nhau;
B.
Vuông góc với nhau.
C.
Trùng nhau;
D.
Cắt nhau nhưng không vuông góc với nhau;
C©u 46 : 
Trong không gian Oxyz cho bốn điểm Trong các mệnh đề sau, mệnh đề nào sai ? 
A.
B.
Bốn điểm A, B, C, D tạo thành một tứ diện
C.
Tam giác BCD đều
D.
Tam giác BCD vuông cân
C©u 47 : 
Cho hai đường thẳng và Đường thẳng đi qua điểm , vuông góc với và cắt có phương trình là:
A.
B.
C.
D.
C©u 48 : 
Cho ba điểm A(3; 2; -2) , B(1; 0; 1) và C(2; -1; 3). Phương trình mặt phẳng đi qua A và vuông góc với BC là:
A.
B.
C.
.
D.
C©u 49 : 
Cho đường thẳng và điểm . Toạ độ hình chiếu của điểm A trên là:
A.
B.
C.
D.
C©u 50 : 
Trong không gian Oxyz cho điểm và đường thẳng . Khoảng cách từ A đến đường thẳng d bằng. 
A.
B.
C.
D.
C©u 51 : 
Trong không gian Oxyz cho hai đường thẳng và . Khẳng định nào sau đây là đúng ?
A.
 trùng nhau.
B.
 cắt nhau.
C.
D.
 chéo nhau.
C©u 52 : 
Khoảng cách giữa hai mặt phẳng và là
A.
B.
C.
D.
C©u 53 : 
Trong không gian với hệ tọa độ Oxyz, giả sử mặt cầu có bán kính nhỏ nhất. Khi đó giá trị của m là:
A.
B.
C.
D.
C©u 54 : 
Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(0; 1; 2), B(2; –2; 1), C(–2; 0; 1). Gọi là điểm thuộc mặt phẳng (P): sao cho MA=MB=MC. Giá trị của là
A.
-2
B.
0
C.
-1
D.
-3
C©u 55 : 
Trong không gian (Oxyz). 
Cho mặt cầu (S):. Gọi I là tâm của mặt cầu (S). Giao điểm của OI và mặt cầu (S) có tọa độ là:
A.
 và 
B.
 và 
C.
 và 
D.
 và 
C©u 56 : 
Cho , , tam giác là
A.
Tam giác vuông cân
B.
Tam giác cân 
C.
Tam giác đều
D.
Tam giác vuông
C©u 57 : 
Trong không gian với hệ toạ độ Oxyz, cho điểm M(0;1;1) và 2 đường thẳng (d1), (d2) với: (d1): ; (d2) là giao tuyến của 2 mặt phẳng (P): và (Q): . Gọi (d) là đường thẳng qua M vuông góc (d1) và cắt (d2). Trong số các điêm A(0;1;1),
 B(-3;3;6), C(3;-1;-3), D(6;-3;0), có mấy điểm nằm trên (d)?
A.
2
B.
0
C.
1
D.
3
C©u 58 : 
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu và ba điểm . Trong ba điểm trên, số điểm nằm bên trong mặt cầu là
A.
1
B.
2
C.
0	
D.
3
C©u 59 : 
Trên mặt phẳng , cho điểm E có hoành độ bằng 1, tung độ nguyên và cách đều mặt phẳng và mặt phẳng . Tọa độ của E là:
A.
B.
C.
D.
C©u 60 : 
Trong không gian Oxyz cho mặt cầu . Trong ba điểm có bao nhiêu điểm thuộc mặt cầu (S) ?
A.
2
B.
0
C.
1
D.
3
C©u 61 : 
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): và mặt cầu (S): x2 + y2 + z2 – 2x – 4y – 6z – 11 = 0. Mặt phẳng (P) cắt mặt cầu (S) theo một đường tròn có chu vi là
A.
B.
C.
D.
C©u 62 : 
Trong không gian cho các điểm , , và . Nếu là hình hộp thì thể tích của nó là:
A.
36 (đvtt)
B.
40 (đvtt) 
C.
42 (đvtt)
D.
38 (đvtt)
C©u 63 : 
Phương trình đường thẳng đi qua hai điểm A(1; 2; -3) và B(3; -1; 1) là:
A.
B.
C.
D.
C©u 64 : 
Cho hai đường thẳng và .
Mặt phẳng chứa hai đường thẳng và có phương trình là:
A.
B.
C.
D.
C©u 65 : 
Trong không gian Oxyz cho ba vectơ . Trong các mệnh đề sau, mệnh đề nào đúng?
A.
B.
 cùng phương
C.
D.
C©u 66 : 
Trong không gian Oxyz cho tam giác ABC có . Độ dài đường cao của tam giác kẻ từ C là 
A.
B.
C.
D.
C©u 67 : 
Trong không gian Oxyz cho điểm và đường thẳng . Hình chiếu của A trên d có tọa độ là
A.
B.
C.
D.
C©u 68 : 
Mặt cầu có tâm I(1; 2; 3) và tiếp xúc với mp(Oxz) là:
A.
B.
C.
D.
C©u 69 : 
Trong không gian với hệ tọa độ Oxyz, cho 3 điểm . Gọi là trực tâm của tam giác. Giá trị của 
A.
4
B.
5
C.
7
D.
6
C©u 70 : 
Cho (P) : 2x – y + 2z – 1 = 0 và A(1; 3; -2). Hình chiếu của A trên (P) là H(a; b; c). Giá trị của a – b + c là :
A.
 .
B.
.
C.
 .
D.
C©u 71 : 
Cho hai điểm A(1; 0; -3) và B(3; 2; 1). Phương trình mặt cầu đường kính AB là:
A.
B.
C.
D.
C©u 72 : 
Trong không gian Oxyz cho , và hai mặt phẳng . Trong các mệnh đề sau, mệnh đề nào đúng?
A.
Mặt phẳng (Q) đi qua A và không song song với (P).
B.
Mặt phẳng (Q) không đi qua A và song song với (P).
C.
Mặt phẳng (Q) đi qua A và song song với (P).
D.
Mặt phẳng (Q) không đi qua A và không song song với (P).
C©u 73 : 
Trong không gian (Oxyz). Cho 2 điểm và đường thẳng d:. Mặt phẳng (P) chứa 2 điểm A, B và song song với d có phương trình là: 
A.
B.
C.
D.
C©u 74 : 
Tọa độ hình chiếu vuông góc của điểm M(2; 0; 1) trên đường thẳng 
d : là :
A.
(-1; -4; 0)
B.
(0; -2; 1)
C.
(2; 2; 3)
D.
(1; 0; 2)
C©u 75 : 
Trong không gian với hệ tọa độ , cho điểm . Trong các phát biểu sau, phát biểu nào sai:
A.
Tọa độ điểm đối xứng với qua trục là .
B.
Khoảng cách từ đến trục bằng 
C.
Khoảng cách từ đến mặt phẳng tọa bằng .
D.
Tọa độ điểm đối xứng với qua mặt phẳng là .
C©u 76 : 
Cho hai điểm A(-3; 1; 2) và B(1; 0; 4). Mặt phẳng đi qua A và vuông góc với đường thẳng AB có phương trình là:
A.
4x + y + 2z + 7 =0
B.
4x – y + 2z + 9 =0
C.
4x – y + 2z – 9 = 0
D.
4x – y – 2z + 17 =0
C©u 77 : 
Cho , , . Tọa độ giao điểm M của trục với mặt phẳng qua là:
A.
B.
C.
D.
C©u 78 : 
Cho ba điểm A(0;1;2), B(3;0;1), C(1;0;0). Phương trình mặt phăng (ABC) là
A.
B.
C.
D.
C©u 79 : 
Trong không gian (Oxyz). Cho điểm và đường thẳng . Đường thẳng qua I vuông góc và cắt có phương trình là:
A.
B.
C.
D.
C©u 80 : 
Vectơ nào sau đây vuông góc với vectơ pháp tuyến của mặt phẳng 2x - y –z =0?
A.
B.
C.
D.
C©u 81 : 
Trong không gian với hệ tọa độ cho 3 điểm , , . Diện tích của tam giác bằng:
A.
B.
C.
D.
ĐÁP ÁN
01
{ ) } ~
28
{ ) } ~
55
{ ) } ~
02
{ | ) ~
29
{ | } )
56
{ | } )
03
{ | ) ~
30
{ | ) ~
57
) | } ~
04
{ ) } ~
31
{ | } )
58
) | } ~
05
{ ) } ~
32
{ ) } ~
59
{ | } )
06
{ ) } ~
33
{ ) } ~
60
{ | ) ~
07
{ ) } ~
34
) | } ~
61
) | } ~
08
) | } ~
35
) | } ~
62
{ | } )
09
) | } ~
36
{ | } )
63
{ | } )
10
) | } ~
37
) | } ~
64
{ | ) ~
11
{ | ) ~
38
{ | } )
65
{ | ) ~
12
{ | } )
39
{ ) } ~
66
{ | ) ~
13
{ ) } ~
40
{ | ) ~
67
{ | ) ~
14
) | } ~
41
{ ) } ~
68
) | } ~
15
) | } ~
42
{ ) } ~
69
) | } ~
16
{ | } )
43
) | } ~
70
{ | } )
17
{ | } )
44
{ | ) ~
71
{ ) } ~
18
) | } ~
45
{ ) } ~
72
{ | ) ~
19
{ | ) ~
46
{ | ) ~
73
{ ) } ~
20
{ | } )
47
{ | ) ~
74
{ | } )
21
) | } ~
48
{ | } )
75
{ | } )
22
{ | } )
49
{ | ) ~
76
{ ) } ~
23
{ | ) ~
50
{ | ) ~
77
{ | } )
24
{ | } )
51
{ | ) ~
78
) | } ~
25
{ | ) ~
52
) | } ~
79
{ ) } ~
26
{ ) } ~
53
) | } ~
80
{ ) } ~
27
) | } ~
54
) | } ~
81
{ | } )