Chuyên đề: Hình học không gian - Ôn Tập THPT Quốc Gia

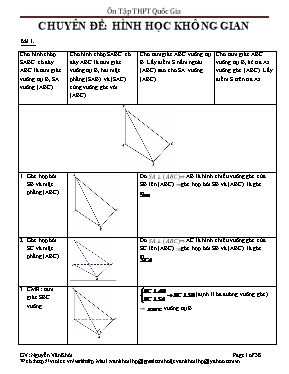
CHUYÊN ĐỀ: HÌNH HỌC KHÔNG GIAN
Bài 1.
Cho hình chóp SABC có đáy ABC là tam giác vuông tại B, SA vuông (ABC)
Cho hình chóp SABC có đáy ABC là tam giác vuông tại B, hai mặt phẳng (SAB) và (SAC) cùng vuông góc với (ABC).
Cho tam giác ABC vuông tại B. Lấy điểm S nằm ngoài (ABC) sao cho SA vuông (ABC)
Cho tam giác ABC vuông tại B, kẻ tia Ax vuông góc (ABC). Lấy điểm S trên tia Ax.
Góc hợp bởi SB và mặt phẳng (ABC)
Do SA⊥(ABC)⇒ AB là hình chiếu vuông góc của SB lên (ABC) ⇒góc hợp bởi SB và (ABC) là góc 
Góc hợp bởi SC và mặt phẳng (ABC)
Do SA⊥(ABC)⇒ AC là hình chiếu vuông góc của SC lên (ABC) ⇒góc hợp bởi SB và (ABC) là góc 
CMR: tam giác SBC vuông
 (định lí ba đường vuông góc). ⇒ vuông tại B.
Góc hợp bởi SC và mặt phẳng (SAB)
⇒ SB là hình chiếu vuông góc của SC lên (SAB)
⇒góc hợp bởi SC và (SAB) là góc 
Góc hợp bởi SB và mặt phẳng (SAC)
Gọi E là hình chiếu vuông góc của B lên AC
⇒ SE là hình chiếu vuông góc của SB lên (SAC)
⇒góc hợp bởi SB và (SAC) là góc 
Góc hợp bởi (SBC) và mặt phẳng (ABC)
 Góc hợp bởi (SBC) và (SAC) là góc tạo bởi hai đường thẳng SB và AB là 
Tính thể tích khối SABC
Xác định tâm và bán kính mặt cầu đi qua 4 điểm S, A, B, C.
Cách 1.
Gọi I là trung điểm SC.
(dựa vào câu 3)
Từ (1) và (2) suy ra 
 I là tâm mặt cầu đi qua 4 điểm S, A, B, C. Với bán kính 
Cách 2: (thực hiện 4 bước tổng quát)
Gọi M là trung điểm của SB, N là điểm trên SC sao cho . Tính thể tích khối 
Ta có: 
Gọi G là trọng tâm tam giác SBC. Mặt phẳng (P) đi qua AG và song song BC, cắt SB, SC tại M, N. Tính thể tích khối AMNCB.
Gọi K là trung điểm BC. G là trọng tâm của tam giác SBC. Trong tam giác SBC qua G kẻ song song BC, cắt SB tại M, SC tại N. 
Ta có: 
Gọi H, K lần lượt là hình chiếu vuông góc của A lên SB và SC. Tính tỉ lệ thể tích của chóp SABC được chia bởi (AHK)
 vuông tại A.
 vuông tại A.
Ta có: 
Tính 
Cách 1:
Gọi H là hình chiếu của A lên SB
Tính AH bằng các công thức sau:
Cách 2: 
Tính 
 (ý 3)
Tính 
Gọi E là hình chiếu vuông góc của B lên AC.
(tính BE như ý 12)
Tính 
Tính 
Gọi P sao cho PACB là hình bình hành 
Gọi K là hình chiếu của A lên BP, H là hình chiếu của A lên SK
Từ (1) và (2) 
Tính 
Gọi P sao cho ABCP là hình bình hành.
Vì là hình chữ nhật.
Gọi H là hình chiếu của A lên SP.
 (1)
 (2)
Từ (1), (2) 
Tính Q thuộc AB sao cho 
Ta có: 
Bài toán quay về ý 12.
Tính . G là trọng tâm cùa tam giác SAB
Gọi M là trung điểm của AB, G là trọng tâm của tam giác SAB.
Từ (1), (2) suy ra 
Bài toán quay về ý 12.
Áp dụng thực tế
, góc hợp bởi SB và (ABC) là 
góc hợp bởi SC và (SAB) là 
Bài 2.
Cho hình chóp SABCD có đáy ABCD là hình vuông. 
Cột thứ 3 chỉ gợi ý. Các em phải nắm rõ bài 1 để trình bày và lý luận.
Góc hợp bởi SB và mặt phẳng (ABCD)
Góc hợp bởi SC và mặt phẳng (ABCD)
Góc hợp bởi SD và mặt phẳng (ABCD)
Góc hợp bởi SC và mặt phẳng (SAB)
Góc hợp bởi SC và mặt phẳng (SAD)
Góc hợp bởi mặt phẳng (SBC) và mặt phẳng (ABCD)
Góc hợp bởi mặt phẳng (SCD) và mặt phẳng (ABCD)
Góc hợp bởi mặt phẳng (SBD) và mặt phẳng (ABCD)
Góc hợp bởi mặt phẳng (SBC) và mặt phẳng (SAB)
Gọi H là hình chiếu vuông góc của A lên SB.
Cách 1:
Cách 2:
Góc hợp bởi mặt phẳng (SCD) và mặt phẳng (SAD)
Tương tự ý 9
Góc hợp bởi mặt phẳng (SBC) và mặt phẳng (SCD)
Cách 1:
Gọi H là hình chiếu vuông góc của B lên SC (khi đó H cũng là hình chiếu vuông góc của D lên SC).
Cách 2:
Gọi M, N lần lượt là hình chiếu vuông góc của A lên SSB, SD.
Tính thể tích các khối:.
Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp SABCD
Gọi I là trung điểm của SC.
 vuông tại A
 vuông tại B
 vuông tại D
Từ (1), (2) và (3) suy ra 
 I là tâm mặt cầu ngoại tiếp hình chóp SABCD với bán kính 
Tính 
Gọi H là hình chiếu vuông góc của A lên SB. 
Tính 
Gọi H là hình chiếu vuông góc của A lên SD. 
Tính 
Gọi H là hình chiếu vuông góc của A lên SO. 
Tính 
Gọi H là hình chiếu vuông góc của A lên SD. 
Do 
Tính với M thuộc AB
Gọi H là hình chiếu vuông góc của A lên SD. 
Do 
Tính 
Gọi H là hình chiếu vuông góc của A lên SD.
Do 
Tính với P là trung điểm BO
Gọi H là hình chiếu vuông góc của A lên SD.
Do 
Do 
Vậy: 
Tính với G là trọng tâm của tam giác SAB
Gọi H là hình chiếu vuông góc của A lên SD. M là trung điểm AB.
Tính 
Gọi H là hình chiếu vuông góc của A lên SB. 
Tính 
Cách 1:
Gọi H là hình chiếu vuông góc của B lên SC. 
Cách 2:
Gọi K là hình chiếu vuông góc của A lên SD. 
Tính 
Gọi H là hình chiếu vuông góc của O lên SC. 
Tính 
Gọi H là hình chiếu vuông góc của A lên SB.
Tính 
Tính . Với M là trung điểm SC
Gọi K là trung điểm AB, H là hình chiếu vuông góc của O lên AK.
Gọi H, I, K lần lượt là hình chiếu vuông góc của A lên SB, SC, SK. CMR: A, H, I, K đồng phẳng. Tính thể tích khối chóp SAHIK
Gợi ý: 
Mà 
Ta có: 
Gọi G là trọng tâm tam giác SBD. (P) qua AG song song BD cắt SB, SC, SD tại M, N, Q. Tính thể tích khối chóp SAMNQ
Áp dụng thực tế
, góc hợp bởi của SC và mặt phẳng (ABCD) là 
, góc hợp bởi của mặt phẳng (SBD) và mặt phẳng (ABCD) là 
, góc hợp bởi của SC và mặt phẳng (SAB) là 
Bài 3:
Cho hình chóp SABCD có đáy ABCD là hình chữ nhật. 
Cột thứ 3 chỉ gợi ý. Các em phải nắm rõ bài 1 để trình bày và lý luận.
Góc hợp bởi SB và mặt phẳng (ABCD)
Hình tương tự bài 2.
Góc hợp bởi SC và mặt phẳng (ABCD)
Hình tương tự bài 2.
Góc hợp bởi SD và mặt phẳng (ABCD)
Hình tương tự bài 2.
Góc hợp bởi SC và mặt phẳng (SAB)
Hình tương tự bài 2.
Góc hợp bởi SC và mặt phẳng (SAD)
Hình tương tự bài 2.
Góc hợp bởi mặt phẳng (SBC) và mặt phẳng (ABCD)
Hình tương tự bài 2.
Góc hợp bởi mặt phẳng (SCD) và mặt phẳng (ABCD)
Hình tương tự bài 2.
Góc hợp bởi mặt phẳng (SBD) và mặt phẳng (ABCD)
Hình tương tự bài 2.
Góc hợp bởi mặt phẳng (SBC) và mặt phẳng (SAB)
Hình tương tự bài 2.
Gọi H là hình chiếu vuông góc của A lên SB.
Cách 1:
Cách 2:
Góc hợp bởi mặt phẳng (SCD) và mặt phẳng (SAD)
Hình tương tự bài 2.
Tương tự ý 9
Góc hợp bởi mặt phẳng (SBC) và mặt phẳng (SCD)
Hình tương tự bài 2.
Cách 1:
Gọi H là hình chiếu vuông góc của B lên SC (khi đó H cũng là hình chiếu vuông góc của D lên SC).
Cách 2:
Gọi M, N lần lượt là hình chiếu vuông góc của A lên SSB, SD.
Tính thể tích các khối:.
Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp SABCD
Hình tương tự bài 2.
Gọi I là trung điểm của SC.
 vuông tại A
 vuông tại B
 vuông tại D
Từ (1), (2) và (3) suy ra 
 I là tâm mặt cầu ngoại tiếp hình chóp SABCD với bán kính 
Tính 
Hình tương tự bài 2.
Gọi H là hình chiếu vuông góc của A lên SB. 
Tính 
Hình tương tự bài 2.
Gọi H là hình chiếu vuông góc của A lên SD. 
Tính 
Hình tương tự bài 2.
Gọi H là hình chiếu vuông góc của A lên SO. 
Tính 
Hình tương tự bài 2.
Gọi H là hình chiếu vuông góc của A lên SD. 
Do 
Tính với M thuộc AB
Hình tương tự bài 2.
Gọi H là hình chiếu vuông góc của A lên SD. 
Do 
Tính 
Hình tương tự bài 2.
Gọi H là hình chiếu vuông góc của A lên SD.
Do 
Tính với P là trung điểm BO
Hình tương tự bài 2.
Gọi H là hình chiếu vuông góc của A lên SD.
Do 
Do 
Vậy: 
Tính với G là trọng tâm của tam giác SAB
Hình tương tự bài 2.
Gọi H là hình chiếu vuông góc của A lên SD. M là trung điểm AB.
Tính 
Hình tương tự bài 2.
Gọi H là hình chiếu vuông góc của A lên SB. 
Tính 
Hình tương tự bài 2.
Cách 1:
Gọi H là hình chiếu vuông góc của B lên SC. 
Cách 2:
Gọi K là hình chiếu vuông góc của A lên SD. 
Tính 
Hình tương tự bài 2.
Gọi H là hình chiếu vuông góc của O lên SC. 
Tính 
Hình tương tự bài 2.
Gọi H là hình chiếu vuông góc của A lên SB.
Tính 
Hình tương tự bài 2.
Tính . Với M là trung điểm SC
Hình tương tự bài 2.
Gọi K là trung điểm AB, H là hình chiếu vuông góc của O lên AK.
Gọi H, I, K lần lượt là hình chiếu vuông góc của A lên SB, SC, SK. CMR: A, H, I, K đồng phẳng. Tính thể tích khối chóp SAHIK
Hình tương tự bài 2.
Gợi ý: 
Mà 
Ta có: 
Gọi G là trọng tâm tam giác SBD. (P) qua AG song song BD cắt SB, SC, SD tại M, N, Q. Tính thể tích khối chóp SAMNQ
Hình tương tự bài 2.
Áp dụng thực tế
, góc hợp bởi của SC và mặt phẳng (ABCD) là 
, góc hợp bởi của mặt phẳng (SBD) và mặt phẳng (ABCD) là 
, góc hợp bởi của SC và mặt phẳng (SAB) là 
Bài 4:
Cho hình chóp tam giác đều SABC. M là trung điểm BC, O là tâm của tam giác ABC.
Góc hợp bởi cạnh bên và mặt đáy
Góc hợp bởi mặt bên và mặt đáy.
Thể tích khối chóp SABC
Tính 
Cách 1:
Cách 2:
Gọi H là hình chiếu vuông góc của O lên SM.
Tính 
Gọi H là hình chiếu vuông góc của M lên SA.
Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp SABC
SO là trục của tam giác ABC. Gọi N là trung điểm SA. Dựng mặt phẳng trung trực của SA cắt SO tại I I là tâm mặt cầu ngoại tiếp hình chóp SABC, bán kính 
Cách 1:
Cách 2:
Tính thể tích khối nón ngoại tiếp khối chóp SABC
Chóp SABC nội tiếp trong hình nón có bán kính ; chiều cao và đường sinh 
Tính thể tích khối trụ ngoại tiếp chóp SABC
Chóp SABC nội tiếp trong hình trụ có bán kính ; chiều cao
Gọi E là trung điểm AB. Tính 
Gọi P sao cho BECP là hình bình hành.
CE vuông AB nên BECP là hình chữ nhật.
Kẻ gọi K thuộc BP sao cho OK song song EB.
Gọi H là hình chiếu của O lên SK.
Gọi E là trung điểm AB. Tính 
Gọi F là trung điểm AC. K giao điểm AM với EF. H là hình chiếu của O lên SK.
Áp dụng thực tế
Cạnh đáy bằng a, cạnh bên bằng 
Cạnh đáy bằng a, cạnh bên hợp với mặt đáy một góc là 
Cạnh đáy bằng 2a, mặt bên hợp với mặt đáy một góc là 
Cạnh đáy bằng , mặt bên hợp với mặt đáy một góc là 
Cạnh đáy bằng a, diện tích tam giác SAC bằng 
Cạnh đáy bằng 2a, khoảng cách từ A đến (SBC) là 
Bài 5:
Cho hình chóp tứ giác đều SABCD. M là trung điểm CD, O là tâm của ABCD.
Góc hợp bởi cạnh bên và mặt đáy
Góc hợp bởi mặt bên và mặt đáy.
Thể tích khối chóp SABCD
Tính 
Gọi H là hình chiếu vuông góc của O lên SM.
Tính 
Gọi H là hình chiếu vuông góc của O lên SM.
Xác định tâm và bán kính của mặt cầu ngoại tiếp hình chóp SABCD
SO là trục của ABCD. Gọi N là trung điểm của SA. Dựng mặt phẳng trung trực của SA cắt SO tại I.
I là tâm mặt cầu ngoại tiếp hình chóp SABCD, bán kính 
Để tính IS ta dùng
Cách 1:
Cách 2: 
Cạnh đáy bằng a, cạnh bên bằng 
Cạnh đáy bằng a, cạnh bên hợp với mặt đáy một góc là 
Cạnh đáy bằng 2a, mặt bên hợp với mặt đáy một góc là 
Bài 6:
Cho hình chóp OABC có OA, OB, OC đôi một vuông góc nhau (tứ diện vuông OABC)
Góc hợp bởi: 
Góc hợp bởi (ABC) và (OBC)
Gọi E là hình chiếu vuông góc của O lên BC. 
Thể tích khối OABC
Gọi H là hình chiếu vuông góc của O lên (ABC). Chứng minh rằng H là trực tâm của tam giác ABC
Kẻ AH cắt BC tại E. Do H là hình chiếu vuông góc của O lên (ABC) nên . Suy ra nên AH là đường cao của tam giác ABC.
Tương tự cho BH; CH.
Vậy H là trực tâm của tam giác ABC.
Chú ý:
Áp dụng thực tế 
Bài 7,
Cho hình chóp SABCD có đáy ABCD là hình thoi. O là giao điểm AC và BD. Hình chiếu của S lên (ABCD) là H thuộc AB sao cho 
Tính thể tích khối chóp SABCD.	
Tính 
Gọi K là hình chiếu vuông góc của H lên CD. J là hình chiếu vuông góc của H lên SK.
Tính 
Gọi K là hình chiếu vuông góc của H lên CD. J là hình chiếu vuông góc của H lên SK.
Tính 
Kẻ đường thẳng d qua D song HC. Gọi K là hình chiếu vuông góc của H lên đường thẳng d. J là hình chiếu vuông góc của H lên SK.
BÀI TẬP HƯỚNG DẪN
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với đáy ,
 SA = a.
Chứng minh rằng các mặt bên hình chóp là những tam giác vuông.
CMR (SAC) (SBD) .
Tính góc giữa SC và mp ( SAB ) .
Tính góc giữa hai mặt phẳng ( SBD ) và ( ABCD)
Tính d(A, (SCD)) .
Giải
Chứng minh rằng các mặt bên hình chóp là những tam giác vuông.
Ta có : 
 vuông tại A.
Chứng minh vuông :
 Ta có : ( Hai cạnh kề của hình vuông ABCD )
	 ( vì )
	 , mà 
 vuông tại B.
 Chứng minh vuông :
Ta có : ( Hai cạnh kề của hình vuông ABCD )
	 (Vì )
 , mà 
 vuông tại D.
CMR (SAC) (SBD) :
	 (Hai đường chéo của hình vuông ABCD )
 ( Vì )
 , mà .
Tính góc giữa SC và mp ( SAB ) :
v Do tại B nên hình chiếu của C lên (SAB) là B.
	 Hình chiếu của SC lên (SAB) là SB.
	.
v Trong vuông tại A, ta có : .
v Trong vuông tại B, ta có : .
Vậy .
Tính góc giữa hai mặt phẳng ( SBD ) và ( ABCD) :
Ta có : .
Gọi O là tâm của hình vuông ABCD, .
Theo chứng minh ở câu b) , mà .
Mặc khác, . 
§ Vậy (do là góc nhọn).
§ .
§ Trong vuông tại A, ta có : .
.
Nhận xét : Để xác định góc giữa và ta có thể làm theo các cách sau :
v Cách 1 : Tìm a, b sao cho .
v Cách 2 : Nếu thì tìm . Từ O, trong vẽ tại O ;
trong vẽ tại O. Suy ra . (đã trình bày ở câu d) )
v Cách 3 : Trong trường hợp tổng quát :
	§ Tìm ;
	§ Tìm sao cho ;
	§ Tìm , ;
	Kết luận : .
Câu d) ta có thể trình bày cách 3 như sau :
	§ Ta có : ;
	§ (theo chứng minh câu b) )
	§ , ;
	Vậy ( Vì là góc nhọn).
Tính d(A, (SCD)) :
Gọi H là hình chiếu của A lên SD.
Ta có : 	(1)
	 ( Hai cạnh kề của hình vuông ABCD) ;
	 (Vì ).
 , mà 	(2)
Từ (1), (2) tại H .
Xét vuông tại A có AH là đường cao :
	Ta có : .
Vậy .
 Cho hình chóp S. ABC có đáy ABC là tam giác vuông tại C và SB (ABC), biết AC = a, BC = a, SB = 3a.
Chứng minh: AC (SBC)
Gọi BH là đường cao của tam giác SBC. Chứng minh: SA BH.
Tính góc giữa đường thẳng SA và mặt phẳng (ABC)
Giải
Chứng minh : AC(SBC)
Ta có : (gt) ;
	 (Vì ) ;
 .
Chứng minh : SA BH
Để chứng minh SA BH ta chứng minh .
Ta có : (gt)	(1)
Theo chứng minh trên , mà (2)
Từ (1) và (2) , mà .
Tính góc giữa đường thẳng SA và mặt phẳng (ABC) 
Do tại B nên hình chiếu của S lên (ABC) là B.
Hình chiếu của SA lên (ABC) là BA.
.
§ Trong vuông tại C, ta có : 
§ Trong vuông tại B, ta có : .
Vậy .
Cho hình chóp S. ABCD có đáy ABCD là hình thoi cạnh a có góc = 600 
và SA=SB = SD = a.
Chứng minh (SAC) vuông góc với (ABCD)
Chứng minh tam giác SAC vuông
Tính khoảng cách từ S đến (ABCD)
Giải
Chứng minh (SAC) vuông góc với (ABCD)
Gọi O là tâm của hình thoi ABCD.
Ta có : cân tại S có O là trung điểm của BD nên 	;	
	ABCD là hình thoi nên ;	
 , mà .
Chứng minh tam giác SAC vuông
Ta chứng minh SO = AO = OC.
§ Do cân tại A có đều.
§ đều cạnh a có AO là đường trung tuyến
.
§ Xét vuông tại O, ta có : .
, mà SO là đường trung tuyến của vuông tại S.
Chú ý : Cho tam giác ABC có AM là đường trung tuyến 
 vuông tại A.
“Trong một tam giác vuông đường trung tuyến ứng với
cạnh huyền bằng một nửa cạnh huyền”
Tính khoảng cách từ S đến (ABCD)
Xét hình chóp S.ABD :
Ta có : SA = SB = SD = a, AB = BD = DA = a nên S.ABD là hình chóp đều.
Gọi H là trọng tâm của (Theo tính chất của hình chóp đều).
 tại H .
§ Vì H là trọng tâm nên .
§ Trong vuông tại H, ta có : .
.
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, mặt bên (SAB) là tam giác đều. Gọi E, F là trung điểm của AB và CD.
a) Cho biết tam giác SCD vuông cân tại S. Chứng minh: SE (SCD) và SF (SAB).
b) Gọi H là hình chiếu vuông góc của S trên EF. Chứng minh: SH AC
c) Tính góc giữa đường thẳng BD và mặt phẳng (SAD)
Giải
Chứng minh SE (SCD) và SF (SAB).
 v Chứng minh SE (SCD) :
§ Do cân tại S có F là trung điểm của CD 	
Mà (theo tính chất của hình vuông)	
, mà 	(1)
§ Ta chứng minh vuông tại S bằng cách
 sử dụng định lý Pytago như sau :
 vuông tại S có SF là đường trung tuyến nên 
.
 đều cạnh a có SE là trung tuyến nên .
EF = a.
Ta có : .
Vậy vuông tại S	(2)
Từ (1) và (2) .
v Chứng minh SF (SAB) :
Theo chứng minh trên, 	(3)
, mà AB // CD 	(4)
Từ (3) và (4) .
Chứng minh SH AC
Ta có : (theo chứng minh trên), mà .
Hơn nữa, (gt) .
Mà .
Tính góc giữa đường thẳng BD và mặt phẳng (SAD) (câu khó - các em học sinh đọc tham khảo).
Gọi O là tâm của hình vuông ABCD.
Theo tính chất của hình vuông ABCD, ta có AC, BD và EF đồng quy tại O.
Vì nên H thuộc đoạn OF.
§ Trong mặt phẳng (ABCD), qua H vẽ đường thẳng song song với CD cắt AD, OD lần lượt tại M và K.
Vậy góc giữa BD và mặt phẳng (SAD) là góc giữa KD và (SAD). Ta đi tìm hình chiếu của K lên (SAD).
Ta có : (do ) .
.
§ Vẽ () tại P.
Nhận xét : Nếu hai mặt phẳng vuông góc với nhau thì đường thẳng nào nằm trong mặt phẳng này và vuông góc với giao tuyến thì vuông góc với mặt phẳng kia.
Hình chiếu của K lên (SAD) là P.
Hình chiếu của KD lên (SAD) là PD.
.
§ Để tìm góc ta đi tìm KD và KP.
§ vuông tại S có SH là đường cao nên ta có : .
§ vuông tại H nên ta có : .
§ .
H là trung điểm của OF, mà HK // DF nên HK là đường trung bình của .
K là trung điểm của OD . (do ).
§ , là trung điểm của MH.
§ Trong (SHM), vẽ (), mà mà K là trung điểm của MH nên KP là đường trung bình của .
§ vuông tại H có HQ là đường cao, ta có :
.
.
§ Trong vuông tại P, ta có : 
Vậy .
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, và SA = 2a.
a). Chứng minh ; 
b). Tính góc giữa SD và (ABCD); SB và (SAD) ; SB và (SAC); 
c). Tính d(A, (SCD)); d(B,(SAC))
Giải
Chứng minh ; 
v Chứng minh :
Ta có : (Hai đường chéo của hình vuông ABCD) ;
	 (do ) ;
 , mà .
v Chứng minh :
Ta có : (Hai cạnh kề của hình vuông ABCD) ;
	 (do ;
 , mà .
Tính góc giữa SD và (ABCD); SB và (SAD) ; SB và (SAC).
v Tính góc giữa SD và (ABCD).
Ta có : tại A nên hình chiếu của S lên mp (ABCD) là A.
Hình chiếu của SD lên mặt phẳng (ABCD) là AD.
.
Trong vuông tại A, 
Vậy .
v Tính góc giữa SB và (SAD).
Ta có : tại A nên hình chiếu của B lên (SAD) là A.
Hình chiếu của SB lên mặt phẳng (SAD) là SA.
.
Trong vuông tại A, 
Vậy .
v Tính góc giữa SB và (SAC).
Gọi O là tâm của hình vuông ABCD.
Theo chứng minh trên tại O nên hình chiếu của B lên (SAC) là O.
Hình chiếu của SB lên (SAC) là SO.
.
§ .
§ vuông tại A nên .
§ Trong vuông tại O, ta có : .
Vậy .
Tính d(A, (SCD)); d(B,(SAC)).
vTính d(A, (SCD)).
Gọi H là hình chiếu vuông góc của A trên SD.
Ta có : .
Theo chứng minh ở câu a, mà .
 tại H .
§ vuông tại A có là đường cao, ta có : .
Vậy .
Nhận xét : Nếu hai mặt phẳng vuông góc với nhau thì đường thẳng nào nằm trong mặt phẳng này và vuông góc với giao tuyến thì vuông góc với mặt phẳng kia.
Trong ý trên, do (SAD) (SCD) và có giao tuyến là SD nên khi kẽ thì .
vTính d(B,(SAC)).
Theo chứng minh trên tại O nên hình chiếu của B lên (SAC) là O.
.
Hình chóp S.ABC. DABC vuông tại A, góc = 600 , AB = a, hai mặt bên (SAB) và (SBC) vuông góc với đáy; SB = 2a. Hạ BH ^ SA (H Î SA); BK ^ SC (K Î SC).
a) CM: SB ^ (ABC)
b) CM: mp(BHK) ^ SC.
c) CM: DBHK vuông .
d) Tính cosin của góc tạo bởi SA và (BHK).
Giải
Nhận xét : Hai mặt phẳng cùng vuông góc với một mặt phẳng thì giao tuyến của chúng (nếu có) vuông góc với mặt phẳng đó, tức là :
Ta có : .
CM SB ^ (ABC) :
Ta có : .
CM (BHK) ^ SC :
§ (gt)	(1)
§( vuông tại A) ; 
 (do ) .
 mà , mặc khác (gt)
mà 	(2)
Từ (1) và (2) .
CM DBHK vuông :
Theo chứng minh ở câu b, mà .
Vậy vuông tại H.
Tính cosin của góc tạo bởi SA và (BHK) :
Vì nên.
Theo chứng minh ở câu b, tại K nên hình chiếu của S lên (BHK) là K.
Hình chiếu của SH lên (BHK) là KH.
§vuông tại K nên . Ta có : .
§ vuông tại A, .
§ vuông tại B nên .
§.
.
Vậy .
 Cho hình chóp tứ giác đều S.ABCD, cạnh đáy bằng a, cạnh bên bằng . Gọi O là tâm của hình vuông ABCD. Và M là trung điểm của SC.
Chứng minh: (MBD) (SAC)
Tính góc giữa SA và mp(ABCD) .
Tính góc giữa hai mặt phẳng ( MBD) và (ABCD).
Tính góc giữa hai mặt phẳng ( SAB) và (ABCD)
Nhắc lại : Hình chóp đều là hình chóp có các cạnh bên bằng nhau và có đáy là đa giác đều. Do đó, trong hình chóp đều, tâm của đa giác đáy trùng với hình chiếu của đỉnh S lên mặt đáy. 
Chứng minh : (MBD) (SAC) :
Vì hình chóp S.ABCD đều nên ;
 mà ;
Hơn nữa, (Hai đường chéo của hình vuông ABCD);
 mà .
Tính góc giữa SA và mp(ABCD) :
Ta có : nên hình chiếu của S lên (ABCD) là O.
Hình chiếu của SA lên (ABCD) là OA.
.
§ ; 
§ Trong vuông tại O, ta có :
 .
Vậy .
Tính góc giữa hai mặt phẳng ( MBD) và (ABCD) :
§ Ta có : ;
§ ;
§ ;
§ ;
( Vì là góc nhọn )
v Trong vuông tại O có OM là đường trung tuyến nên .
v .
v Áp dụng định lí cosin trong tam giác COM, ta có : .
.
Vậy 
Cách 2 : 
Trong vuông tại O có OM là đường trung tuyến nên .
 cân tại M .
Mặc khác, ( Vì cân tại S) . Theo câu b, .
Từ đó suy ra 
Nhận xét : Trong việc xác định góc giữa hai mặt phẳng ( MBD) và (ABCD) ta có thể dùng cách 2 như đã nói ở bài tập 1. Cách này không đơn giản vì tìm điểm thuộc BD đ