Chuyên để: Hệ thức liên hệ giữa cạnh và góc trong tam giác vuông

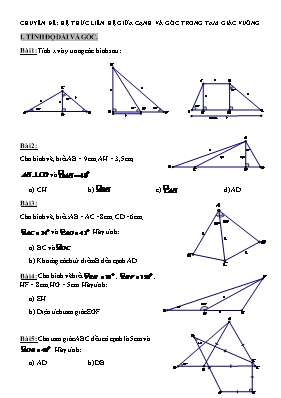
CHUYÊN ĐỂ: HỆ THỨC LIÊN HỆ GIỮA CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG
I. TÍNH ĐỘ DÀI VÀ GÓC.
Bài 1: Tính x và y trong các hình sau:
Bài 2:
Cho hình vẽ, biết AB = 9cm; AH = 3,5cm; 
 và 
CH	b) 	c) 	d) AD.
Bài 3:
Cho hình vẽ, biết: AB = AC =8cm; CD =6cm; 
 và . Hãy tính:
BC và 
Khoảng cách từ điểm B đến cạnh AD.
Bài 4: Cho hình vẽ biết ; ; HF = 8cm; HG = 5cm. Hãy tính:
EH.
Diện tích tam giác EGF.
Bài 5: Cho tam giác ABC đều có cạnh là 5cm và . Hãy tính:
AD.	b) DB.
Bài 6: Tứ giác ABCD có AB = BC; AD = DC.
Biết BC = 15cm; ; . Tính
AD	b) SABCD
Bài 7: Cho hình vẽ. Biết , 
, AD = 2,8cm; AF = 5,5cm, BF =4,1cm
Tính AC.
Gọi E là điểm thuộc AC sao cho DE//BF. Tính EF ?
Tính diện tích tam giác BCF.
Bài 8: Cho tam giác ABC có ; ; AB = 6m. Đường vuông góc kẻ từ C đến AB cắt AB tại H. Tính 
AH, BH. 	b) CH.
Bài 9: Cho tam giác ABC có BC = 12cm; . Hãy tính
Đường cao CH và cạnh AC	b) SABC ?
Bài 10: Tính diện tích của hình bình hành có hai cạnh 12cm và 15cm, góc tạo bởi hai cạnh ấy bằng 1080.
Bài 11: Tính diện tích hình thang cân biết hai cạnh đáy là 15cm và 25cm và góc ở một đáy bằng 700.
Bài 12: Cho một tam giác có các cạnh có độ dài lần lượt là 5,7,9 kẻ đường cao đến cạnh lớn nhất. Hãy tìm độ dài đường cao này và các đoạn thẳng mà nó định ra trên cạnh lớn nhất đó.
Bài 13: Hãy tìm độ dài cạnh đáy của một tam giác cân, nếu biết đường cao kẻ xuống đáy có độ dài là 5cm và đường cao kẻ xuống cạnh bên có độ dài là 6cm.
Bài 14: Cho hình thang có đáy nhỏ là 15cm, hai cạnh bên bằng nhau và bằng 25cm, góc tù bằng 1200. Tính chu vi và diện tích của hình thang đó.
Bài 15: Cho tam giác ABC vuông tại A, AB = 6cm; AC = 8cm.
Tính BC; .
Phân giác của góc A cắt BC tại D. Tính BD, CD.
Từ D kẻ DE và DF lần lượt vuông góc với AB và AC. Tứ giác AEDF là hình gì ? Tính chu vi và diện tích của tứ giác AEDF.
Bài 16: Cho tam giác ABC cân, AB =AC=10cm; BC = 16cm. Trên đường cao AH lấy điểm I sao cho . Vẽ Cx//AH, Cx cắt tia BI tại D.
Tính các góc của tam giác ABC.
Tính diện tích tứ giác ABCD.
Bài 17: Cho tam giác ABC có ; BC = 12cm; AB = 6cm. Đường phân giác của góc B cắt cạnh AC tại D.
Tính BD	b) Gọi M là trung điểm của BC. Chứng minh .
Bài 18: Cho tam giác ABC vuông tại A, đường cao AH , BH = 9cm; CH = 4cm. Gọi D và E lần lượt là hình chiếu của H trên AB và AC.
Tính độ dài DE.
Các đường thẳng vuông góc với DE tại D và tại E lần lượt cắt BC tại M và N. Chứng minh M là trung điểm của BH và N là trung điểm của CH.
Tính diện tích tứ giác DENM.
Bài 19: Cho tam giác ABC vuông tại A, ; BC = 10cm.
Tính AB và AC.
Từ A kẻ AM, AN lần lượt vuông góc với các đường phân giác trong và ngoài của góc B. Chứng minh rằng : MN//BC và MN = AB.
Chứng minh: tam giác MAB và ABC đồng dạng. Tìm tỉ số đồng dạng.
Bài 20: Tam giác ABC có 3 đường cao AD, BE, CF. Chứng minh rằng :
AE.BF.CD = AB.BC.CA.cosA.cosB.cosC.
II. BÀI TOÁN CÓ NỘI DUNG THỰC TẾ
Bài 1: Từ đỉnh một tòa nhà cao 50m, người ta nhìn thấy một ô tô đang đỗ dưới một góc 400 so với đường nằm ngang. Hỏi chiếc ô tô đang đỗ cách tòa nhà đó bao nhiêu mét ?
Bài 2: Một người đứng ở mặt đất cách tòa nhà 150m. Biết rằng người đó nhìn thấy đỉnh của tòa nhà ở góc 200 so với đường nằm ngang, khoảng cách từ mắt đến mặt đất bằng 1,5m. Hãy tính chiều cao của tòa nhà.
Bài 3: Một khách du lịch đứng cách tháp Eiffel 250m, tính góc mà người đó nhìn thấy đỉnh tháp so với đường nằm ngang. Biết tháp Eiffel cao 301m và khoảng cách từ mắt người đó xuống mặt đất là 1,6m. (làm tròn độ).
Bài 4: Một thám tử đứng cách một tòa nhà khoảng 20m. Góc “nâng” từ chỗ anh ta đứng đến nóc tòa nhà là 380.
Tính chiều cao của tòa nhà (làm tròn đến chữ số thập phân thứ hai).
Nếu người này dịch chuyển sao cho góc nâng là 320 thì anh ta cách tòa nhà bao nhiêu mét ? Khi đó anh ta phải tiến lại gần hay ra xa ngôi nhà đó ?
Bài 5: Một cái thang dài 4m tựa vào tường và làm thành góc 700 so với mặt đất. Hỏi chiều cao của thang đạt được so với mặt đất ?
Bài 6: Một người muốn mua một cái thang để sử dụng, biết trần nhà của anh ta cao khoảng 3,8m, góc dựng thang an toàn là khoảng từ 650 đến 800 so với mặt đất. Vậy người này sẽ chọn mua thang có chiều dài như thế nào thì hợp lí ?
Bài 7: Tìm chiều dài của dây kéo cờ, biết bóng của cột cờ là 12,2m và góc nhìn mặt trời là 38049’.
Bài 8: Một cánh diều bị vướng trên cành cây cao 6,25m. Để lấy diều xuống cần phải đặt thang sao cho đầu thang đạt độ cao đó. Khi đó góc của thang tạo với mặt đất là bao nhiêu biết chiếc thang dài 6,58m.
Bài 9: Một máy bay đang bay ở độ cao 10km. Khi máy bay hạ cánh xuống mặt đất, đường đi của máy bay tạo một góc nghiêng so với mặt đất.
Nếu phi công muốn tạo góc nghiêng 30 thì cách sân bay bao nhiêu km phải bắt đầu cho hạ cánh.
Nếu cách sân bay 300km máy bay bắt đầu hạ cánh thì góc nghiêng là bao nhiêu ?
Bài 10: Một tàu ngầm đang ở trên mặt biển sau đó lặn xuống theo phương tạo với mặt nước biển một góc 210.
Nếu tàu chuyển động theo phương lặn xuống được 300m thì khi đó nó ở độ sâu bao nhiêu ? Khi đó khoảng cách theo phương nằm ngang so với nơi xuất phát là bao nhiêu ?
Tàu phải chạy bao nhiêu mét để đạt đến độ sâu 1000m ?
Bài 11: Từ đỉnh một ngọn đèn hải đăng cao 38m so với mặt nước biển, người ta nhìn thấy một hòn đảo dưới góc 300 so với đường nằm ngang chân đèn. Hỏi khoảng cách từ hòn đảo đến chân đèn (ở mực nước biển) bằng bao nhiêu ?