Chuyên đề 1: Phương trình lượng giác - Trường THPT Ngô Gia Tự

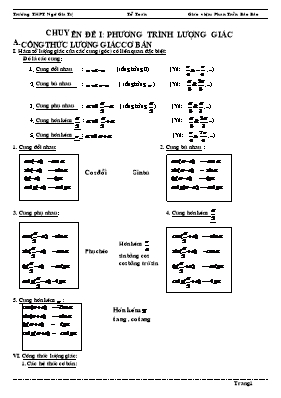
 CHUYÊN ĐỀ I: PHƯƠNG TRÌNH LƯỢNG GIÁC	 A.CƠNG THỨC LƯỢNG GIÁC CƠ BẢN
I. Hàm số lượng giác của các cung (góc) có liên quan đặc biệt:
 Đó là các cung :
	1. Cung đối nhau : (tổng bằng 0) (Vd: ,)
	2. Cung bù nhau : ( tổng bằng ) (Vd: ,)
	3. Cung phụ nhau : ( tổng bằng ) (Vd: ,)
	4. Cung hơn kém : (Vd: ,)
 	5. Cung hơn kém : (Vd: ,)
1. Cung đối nhau: 2. Cung bù nhau : 
Sin bù
Cos đối
3. Cung phụ nhau : 4. Cung hơn kém 
Phụ chéo
Hơn kém 
sin bằng cos
cos bằng trừ sin
Hơn kém 
tang , cotang
5. Cung hơn kém :
VI. Công thức lượng giác:
 1. Các hệ thức cơ bản:
 2. Công thức cộng :
 3. Công thức nhân đôi:
5. Công thức hạ bậc:
 6.Công thức tính theo 
 7. Công thức biến đổi tích thành tổng :
 8. Công thức biến đổi tổng thành tích :
 9. Các công thức thường dùng khác 
B.PHUƯƠNG TRÌNH LƯỢNG GIÁC
DẠNG I: PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
A.CƠNG THỨC NGHIỆM CẦN NHỚ
 Cơng thức nghiệm 
 Các trường hợp đặc biệt 
( u; v là các biểu thức chứa ẩn và )
B.BÀI TẬP ÁP DỤNG
 Bài 1: GIẢI CÁC PHƯƠNG TRÌNH LƯỢNG GIÁC SAU
 a) b) c) d) 
1) 2sin(3x-)- 2) cos 3) 
 4) 5) 
 6) 7) 8) 
Bài 2: Tìm nghiệm của phương trình trên các khoảng cho trước
 b) , với 
c) sin(2x - 10o) = víi -120o < x < 90o d) cos(2x + 1) = víi - p < x < p	
DẠNG 2: PHƯƠNG TRÌNH BẬC 2 ĐỐI VỚI 1 HÀM SỐ LƯỢNG GIÁC
A.LÝ THUYẾT CẦN NHỚ
Dạng phương trình
Phương pháp giải
Đặt ẩn phụ : t = sinx ( t = cosx; t = tgx; t = cotgx)
Ta được phương trình : (1)
Giải phương trình (1) tìm t, rồi suy ra x
 Chú ý : Nếu thì điều kiện 
B.BÀI TẬP ÁP DỤNG:
Bài 1: Giải các phương trình sau
1) 	 2) 3)	
4) 5) 	 6) 
7) 8) 
9) 10) 	
Bài 2: Giải các phương trình sau
d) e) 
f) g) h) 
Bài 3: Tìm nghiệm của phương trình trên các khoảng cho trước
 , 
DẠNG 3: PHƯƠNG TRÌNH BẬC NHẤT ĐỐI VỚI SINX VÀ COSX
A.KIẾN THỨC CẦN NHỚ
Dạng phương trình
Phương pháp giải
Chú ý:
-Phương trình cĩ nghiệm 
-Trong trường hợp phương trình cho dưới dạng: , với cách đặt như bên, phương trình được đưa về dạng
Vậy tùy theo dạng của phương trình, khi áp dụng cơng thức cộng ta sẽ đưa về các phương trình cơ bản khác nhau.
-Ngồi ra ta cịn cĩ thể đặt .
 Chia hai vế của phương trình cho thì pt
 (2)
Đặt với thì :
 Pt (3) có dạng 1. Giải pt (3) tìm x.
B.BÀI TẬP ÁP DỤNG
Bài 1: Giải các phương trình sau:
 3. cos3x + sin3x = ;
4). 4sinx – 3cosx = 5; 5) 3sin2x + 2cos2x = 3; 
Bài 2: Giải các phương trình sau:
 1) 2(sinx + cosx)cosx = 3 + cos2x 
DẠNG 4: PHƯƠNG TRÌNH BẬC 2 ĐỐI VỚI SINX VÀ COSX
Dạng phương trình
Phương pháp giải
Chú ý
- Nếu a = d thì là nghiệm của phuơng trình (4),ngược lại nĩ khơng là nghiệm.
- Ngồi cách giải đưa về phương trình bậc 2 theo tanx, ta cịn cĩ thể dùng các cơng thức
-Hạ bậc: , 
-Nhân đơi: 
Đưa phương trình (4) về dạng (3) : phương trình bậc 1 theo sin2x và cos2x.
Th1: Xét thay vào phương trình, nếu thõa mãn thì là nghiệm của phương trình ngược lại khơng là nghiệm của phương trình.
Th 2: Xét , chia 2 vế của phương trình cho ta được
(*) là phương trình bậc 2 theo tanx đã biết cách giải
KL: Hợp nghiệm của 2 trường hợp.
B. BÀI TẬP ÁP DỤNG
Bài 1: Giái các phương trình sau
Bài 2: Giải các phương trình sau
a) , b) 
c) , d) , 
e) f) .
g) , i) .
h) k) 
Bài 3: Giải các phương trình sau: (***)
DẠNG 5: PHƯƠNG TRÌNH ĐỐI XỨNG
Dạng phương trình
Phương pháp giải
Đặt 
Điều kiện: 
pt
Giải ra t ( chú ý chọn nghiệm t thỏa mãn điều kiện ) giải ra x.
Chú ý:
-Nghiệm t chon được phải thõa mãn điều kiện
Đặt 
Giải tương tự như dạng 1
Đặt 
ĐK: Giải tương tự như dạng 1
Đặt 
ĐK: Giải tương tự như dạng 1
B.BÀI TẬP ÁP DỤNG
ĐÁP ÁN: 
 GIÁO ÁN CĨ SỬ DỤNG TÀI LIỆU CỦA CÁC ĐỒNG NGHIÊP.