Chứng minh định lý đường trung bình trong tam giác bằng kiến thức Toán lớp 7

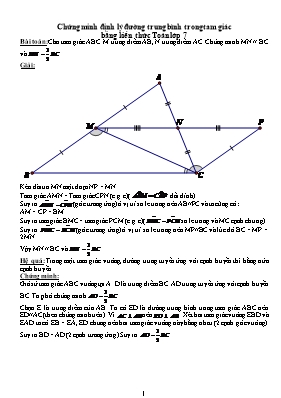
Chứng minh định lý đường trung bình trong tam giác
bằng kiến thức Toán lớp 7
Bài toán: Cho tam giác ABC. M trung điểm AB, N trung điểm AC. Chứng minh MN // BC và .
Giải:
Kéo dài tia MN một đoạn NP = MN. 
Tam giác AMN = Tam giác CPN (c.g.c) ( đối đỉnh)
Suy ra (góc tương ứng) ở vị trí so le trong nên AB//PC và ta cũng có:
AM = CP = BM.
Suy ra tam giác BMC = tam giác PCM (c.g.c) (so le trong và MC cạnh chung).
Suy ra (góc tương ứng) ở vị trí so le trong nên MP//BC và lúc đó BC = MP = 2MN. 
Vậy MN // BC và .
Hệ quả: Trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền thì bằng nửa cạnh huyền.
Chứng minh:
Giả sử tam giác ABC vuông tại A. D là trung điểm BC. AD trung tuyến ứng với cạnh huyền BC. Ta phải chứng minh .
Chọn E là trung điểm của AB. Ta có ED là đường trung bình trong tam giác ABC nên ED//AC (theo chứng minh trên). Vì nên . Xét hai tam giác vuông EBD và EAD ta có EB = EA, ED chung nên hai tam giác vuông này bằng nhau (2 cạnh góc vuông). Suy ra BD = AD (2 cạnh tương ứng). Suy ra .
Áp dụng:
Trích từ:
BỘ ĐỀ ÔN TẬP KIỂM TRA HỌC KÌ 1
MÔN TOÁN LỚP 7 *Thời gian: 90 phút*
ĐỀ 2:
Bài 5: (3,5 điểm) Cho góc nhọn xAy, trên tia Ay lấy điểm B, trên tia Ax lấy điểm C sao cho AB = AC. Gọi M là trung điểm của đoạn thẳng BC và E là trung điểm của đoạn thẳng AC, trên tia đối của tia EM lấy điểm H sao cho EH = EM.
Chứng minh ΔABM = ΔACM
Chứng minh 
Chứng minh ΔAEH = ΔCEM
Gọi D là trung điểm của đoạn thẳng AB. Từ B vẽ đường thẳng song song với đường thẳng AM, đường thẳng này cắt tia MD tại K. Chứng minh ba điểm H, A, K thẳng hàng.
Giải:
a) (c.g.c) (1)
b) (1) => =>(2)
c) (c.g.c) (3).
d) (3) => ở vị trí so le trong nên => AH//BC (4)
Trong tam giác vuông AMB, MD trung tuyến ứng với cạnh huyền AB nên (5)
Từ BK//AM (gt) và (5) =>=> DK = DB => (c.g.c) => ở vị trí so le trong nên => AK//BC (6).
Từ (4) và (6), theo tiên đề Ơclit ta có đường thẳng AH trùng với đường thẳng AK => H, A, K thẳng hàng.
(Nếu không dùng 2 định lý và hệ quả trên thì cũng có thể giải được bài này nhưng hơi dài!:
Phải xét 4 cặp tam giác bằng nhau là:
; ;và )