Câu hỏi trắc nghiệm Giải tích 12 - Hàm số, phương trình mũ và lôgarit

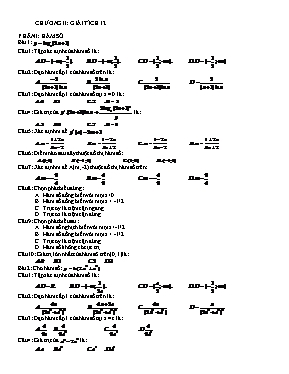
CHƯƠNG II: GIẢI TÍCH 12
PHẦN I: HÀM SỐ
Bài 1: 
Câu 1: Tập xác định của hàm số là:
Câu 2: Đạo hàm cấp 1 của hàm số trên là:
Câu 3: Đạo hàm cấp 1 của hàm số tại x = 0 là:
Câu 4: Giá trị của là: 
Câu 5: Xác định m để 
Câu 6: Điểm nào sau đây thuộc đồ thị hàm số: 
Câu 7: Xác định m để A(m; -2) thuộc đồ thị hàm số trên: 
Câu 8: Chọn phát biểu đúng:
Hàm số đồng biến với mọi x>0.
Hàm số đồng biến với mọi x > -1/2
Trục oy là tiệm cận ngang
Trục ox là tiệm cận đứng
Câu 9: Chọn phát biểu sai:
Hàm số nghịch biến với mọi x>-1/2.
Hàm số đồng biến với mọi x > -1/2
Trục oy là tiệm cận đứng
Hàm số không có cực trị
Câu 10: Giá trị lớn nhất của hàm sô trên [0;1] là:
Bài 2: Cho hàm số: 
Câu 1: Tập xác định của hàm số là:
Câu 2: Đạo hàm cấp 1 của hàm số trên là:
Câu 3: Đạo hàm cấp 1 của hàm số tại x = e là:
Câu 4: Giá trị của là: 
Câu 5: Xác định m để 
Câu 6: Điểm nào sau đây không thuộc đồ thị hàm số: 
Câu 7: Xác định m để A(m; 2) thuộc đồ thị hàm số trên: 
Câu 8: Chọn phát biểu đúng:
Hàm số đồng biến với mọi x>0.
Hàm số đồng biến với mọi x <0
Hàm số đồng biến với mọi x.
Hàm số nghịch biến với mọi x>0.
Câu 9: Chọn phát biểu sai:
Hàm số nghịch biến với mọi x
Hàm số nghịch với mọi x <0
Hàm số có 1 cực trị
Đồ thị hàm số không đi qua gốc tọa độ.
Câu 10: Gọi a và b lần lượt là giá trị lơn nhất và bé nhất của hàm số trên [0;e]. khi đó 
	Tổng a + b là:
	A.1+ln2	B. 2+ln2	C. 3+ln2	D.4+ln2
Bài 3: Cho hàm số 
Câu 1: Tập xác định của hàm số trên là:
Câu 2: Đạo hàm cấp 1 của hàm số trên là:
Câu 3: Đạo hàm cấp 1 của hàm số tại x = 1 là:
Câu 4: T́m x biết là: 
Câu 5: Xác định m để 
Câu 6: Điểm nào sau đây không thuộc đồ thị hàm số: 
Câu 7: Xác định m để A(m; 1) thuộc đồ thị hàm số trên: 
Câu 8: Nghiệm của bất phương tŕnh y < 1/49 là:
Câu 9: Tập nghiệm của bất phương tŕnh y/ < 0 là:
Câu 10: Giá trị nhỏ nhất của hàm số trên [0;1] là:
Bài 4: Cho hàm số 
Câu 1: Đạo hàm của hàm số tại x = 1là:
Câu 2: Chọn khẳng định sai trong các khẳng định sau:
Câu 3: Chọn khẳng định đúng:
Hàm số có đạo hàm tại x = 0.
Hàm số không có đạo hàm tại x = 1.
Đồ thị của hàm số không đi qua Q(1;2e+1).
Hàm số xác định với mọi x dương.
BÀI TẬP HỖ TRỢ
Bài 1: T́m giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
Bài 2: Cho hàm số: . T́m TXD, CMR 
Bài 3: Cho hàm số: . Giải phương tŕnh 
Bài 4: T́m tập xác định, tính của các hàm số sau:
CÁC CÂU TRẮC NGHIỆM TRỰC TIẾP
Hµm sè mò - hµm sè l«garÝt
C©u1: T×m mÖnh ®Ò ®óng trong c¸c mÖnh ®Ò sau:
	A. Hµm sè y = ax víi 0 < a < 1 lµ mét hµm sè ®ång biÕn trªn (-¥: +¥)
	B. Hµm sè y = ax víi a > 1 lµ mét hµm sè nghÞch biÕn trªn (-¥: +¥)
	C. §å thÞ hµm sè y = ax (0 < a ¹ 1) lu«n ®i qua ®iÓm (a ; 1)
	D. §å thÞ c¸c hµm sè y = ax vµ y = (0 < a ¹ 1) th× ®èi xøng víi nhau qua trôc tung
C©u2: Cho a > 1. T×m mÖnh ®Ò sai trong c¸c mÖnh ®Ò sau: 
	A. ax > 1 khi x > 0
	B. 0 < ax < 1 khi x < 0
	C. NÕu x1 < x2 th× 
	D. Trôc tung lµ tiÖm cËn ®øng cña ®å thÞ hµm sè y = ax
C©u3: Cho 0 < a < 1. T×m mÖnh ®Ò sai trong c¸c mÖnh ®Ò sau: 
	A. ax > 1 khi x < 0
	B. 0 0
	C. NÕu x1 < x2 th× 
	D. Trôc hoµnh lµ tiÖm cËn ngang cña ®å thÞ hµm sè y = ax
C©u4: T×m mÖnh ®Ò ®óng trong c¸c mÖnh ®Ò sau: 
	A. Hµm sè y = víi 0 < a < 1 lµ mét hµm sè ®ång biÕn trªn kho¶ng (0 ; +¥)
	B. Hµm sè y = víi a > 1 lµ mét hµm sè nghÞch biÕn trªn kho¶ng (0 ; +¥)
	C. Hµm sè y = (0 < a ¹ 1) cã tËp x¸c ®Þnh lµ R 
	D. §å thÞ c¸c hµm sè y = vµ y = (0 < a ¹ 1) th× ®èi xøng víi nhau qua trôc hoµnh
C©u5: Cho a > 1. T×m mÖnh ®Ò sai trong c¸c mÖnh ®Ò sau:
	A. > 0 khi x > 1
	B. < 0 khi 0 < x < 1
	C. NÕu x1 < x2 th× 
	D. §å thÞ hµm sè y = cã tiÖm cËn ngang lµ trôc hoµnh
C©u6: Cho 0 < a < 1T×m mÖnh ®Ò sai trong c¸c mÖnh ®Ò sau:
	A. > 0 khi 0 < x < 1
	B. 1
	C. NÕu x1 < x2 th× 
	D. §å thÞ hµm sè y = cã tiÖm cËn ®øng lµ trôc tung
C©u7: Cho a > 0, a ¹ 1. T×m mÖnh ®Ò ®óng trong c¸c mÖnh ®Ò sau: 
	A. TËp gi¸ trÞ cña hµm sè y = ax lµ tËp R
	B. TËp gi¸ trÞ cña hµm sè y = lµ tËp R
	C. TËp x¸c ®Þnh cña hµm sè y = ax lµ kho¶ng (0; +¥)
	D. TËp x¸c ®Þnh cña hµm sè y = lµ tËp R
C©u8: Hµm sè y = cã tËp x¸c ®Þnh lµ:
	A. (0; +¥)	B. (-¥; 0)	C. (2; 3)	D. (-¥; 2) È (3; +¥)
C©u9: Hµm sè y = cã tËp x¸c ®Þnh lµ:
	A. (-¥; -2)	B. (1; +¥)	C. (-¥; -2) È (2; +¥)	D. (-2; 2)
C©u10: Hµm sè y = cã tËp x¸c ®Þnh lµ:
	A. 	B. 	C. 	D. R
C©u11: Hµm sè y = cã tËp x¸c ®Þnh lµ:
	A. (0; +¥)\ {e}	B. (0; +¥)	C. R	D. (0; e)
C©u12: Hµm sè y = cã tËp x¸c ®Þnh lµ:
	A. (2; 6)	B. (0; 4)	C. (0; +¥)	D. R
C©u13: Hµm sè y = cã tËp x¸c ®Þnh lµ:
	A. (6; +¥)	B. (0; +¥)	C. (-¥; 6)	D. R
C©u14: Hµm sè nµo díi ®©y ®ång biÕn trªn tËp x¸c ®Þnh cña nã?
	A. y = 	B. y = 	C. y = 	D. y = 
C©u15: Hµm sè nµo díi ®©y th× nghÞch biÕn trªn tËp x¸c ®Þnh cña nã?
	A. y = 	B. y = 	C. y = 	D. y = 
C©u16: Sè nµo díi ®©y nhá h¬n 1?
	A. 	B. 	C. 	D. 
C©u17: Sè nµo díi ®©y th× nhá h¬n 1?
	A. 	B. 	C. 	D. 
C©u18: Hµm sè y = cã ®¹o hµm lµ:
	A. y’ = x2ex	B. y’ = -2xex	C. y’ = (2x - 2)ex	D. KÕt qu¶ kh¸c 
C©u19: Cho f(x) = . §¹o hµm f’(1) b»ng :
	A. e2	B. -e	C. 4e	D. 6e
C©u20: Cho f(x) = . §¹o hµm f’(0) b»ng:
	A. 4	B. 3	C. 2	D. 1
C©u21: Cho f(x) = ln2x. §¹o hµm f’(e) b»ng:
	A. 	B. 	C. 	D. 
C©u22: Hµm sè f(x) = cã ®¹o hµm lµ:
	A. 	B. 	C. 	D. KÕt qu¶ kh¸c 
C©u23: Cho f(x) = . §¹o hµm f’(1) b»ng:
	A. 1	B. 2	C. 3	D. 4
C©u24: Cho f(x) = . §¹o hµm f’ b»ng:
	A. 1	B. 2	C. 3	D. 4
C©u25: Cho f(x) = . §¹o hµm b»ng:
	A. 1	B. 2	C. 3	D. 4
C©u26: Cho y = . HÖ thøc gi÷a y vµ y’ kh«ng phô thuéc vµo x lµ:
	A. y’ - 2y = 1	B. y’ + ey = 0	C. yy’ - 2 = 0	D. y’ - 4ey = 0
C©u27: Cho f(x) = . §¹o hµm f’(0) b»ng:
	A. 1	B. 2	C. 3	D. 4
C©u28: Cho f(x) = . §¹o hµm f’(0) b»ng:
	A. 0	B. 1	C. 2	D. 3
C©u29: Cho f(x) = . §¹o hµm f’(0) b»ng:
	A. 2	B. ln2	C. 2ln2	D. KÕt qu¶ kh¸c 
C©u30: Cho f(x) = tanx vµ j(x) = ln(x - 1). TÝnh . §¸p sè cña bµi to¸n lµ:
	A. -1	B.1 	C. 2	D. -2
C©u31: Hµm sè f(x) = cã ®¹o hµm f’(0) lµ:
	A. 0	B. 1	C. 2	D. 3
C©u32: Cho f(x) = 2x.3x. §¹o hµm f’(0) b»ng:
	A. ln6	B. ln2	C. ln3	D. ln5
C©u33: Cho f(x) = . §¹o hµm f’(1) b»ng:
	A. p(1 + ln2)	B. p(1 + lnp)	C. plnp	D. p2lnp 
C©u34: Hµm sè y = cã ®¹o hµm b»ng:
	A. 	B. 	C. cos2x	D. sin2x
C©u35: Cho f(x) = . §¹o hµm f’(1) b»ng:
	A. 	B. 1 + ln2	C. 2	D. 4ln2
C©u36: Cho f(x) = . §¹o hµm f’(10) b»ng:
	A. ln10	B. 	C. 10	D. 2 + ln10
C©u37: Cho f(x) = . §¹o hµm cÊp hai f”(0) b»ng:
	A. 1	B. 2	C. 3	D. 4
C©u38: Cho f(x) = . §¹o hµm cÊp hai f”(e) b»ng:
	A. 2	B. 3	C. 4	D. 5
C©u39: Hµm sè f(x) = ®¹t cùc trÞ t¹i ®iÓm:
	A. x = e	B. x = e2	C. x = 1	D. x = 2
C©u40: Hµm sè f(x) = ®¹t cùc trÞ t¹i ®iÓm:
	A. x = e	B. x = 	C. x = 	D. x = 
C©u41: Hµm sè y = (a ¹ 0) cã ®¹o hµm cÊp n lµ:
	A. 	B. 	C. 	D. 
C©u42: Hµm sè y = lnx cã ®¹o hµm cÊp n lµ:
	A. 	B. 	C. 	D. 
C©u43: Cho f(x) = x2e-x. bÊt ph¬ng tr×nh f’(x) ≥ 0 cã tËp nghiÖm lµ:
	A. (2; +¥)	B. [0; 2]	C. (-2; 4]	D. KÕt qu¶ kh¸c 
PHẦN II: MŨ VÀ LOGARIT
Bài 1: Cho biểu thức A = 
Câu 1: Khi th́ giá trị của biểu thức A là:
Câu 2: Biểu thức A được rút gọn thành:
Câu 3: Cho x thỏa măn . Khi đó giá trị của A là:
Câu 4: Tìm x biết A > 18.
Câu 5: Tìm x biết 
Câu 6: Tìm x biết .
Câu 7: Tìm x biết 
Câu 8: Tìm x biết 
Câu 9: Tìm x nguyên để A là ước của 9;
Câu 10: Biết rằng x nguyên dương và A là ước của 18. Khi đó giá trị của
	là:
Câu 11: Nếu đặt . Th́ A trở thành
Câu 12: Nếu đặt . Th́ A trở thành
Câu 13: Nếu đặt . Th́ A trở thành
Câu 14: Biểu thức A được rút gọn thành
	D. A, B, C đều đúng
Câu 15: Với x thỏa măn . Xác định m biết A = 9.
Câu 16: Với x thỏa măn với m > 0. Xác định giá trị của m biết A = 36 .
Câu 17: Xác định giá trị của m để giá trị của biểu thức không phụ thuộc vào giá trị của x.
Câu 18: Đặt với A = 9 th́ giá trị của t là:
Câu 19: Với t là số tự nhiên, đặt với A<18 th́ giá trị của t là:
Câu 20: Giá trị lớn nhất của biểu thức L = 5+A với là:
Câu 21: Giá trị bé nhất của biểu thức B = 5-A với là:
Câu 22: Đặt x = sint, khi A = 9 th́ giá trị của t là:
Câu 23: Đặt x = cos2t, khi A = 9 th́ giá trị của t là:
BÀI TẬP HỖ TRỢ
RÚT GỌN CÁC BIỂU THỨC SAU:
CÁC CÂU HỎI TRỰC TIẾP
C©u1: TÝnh: K = , ta ®îc:
	A. 12	B. 16	C. 18	D. 24
C©u2: TÝnh: K = , ta ®ưîc 
	A. 10	B. -10	C. 12	D. 15
C©u3: TÝnh: K = , ta ®ưîc
	A. 	B. 	C. 	D. 
C©u4: TÝnh: K = , ta ®ưîc
	A. 90	B. 121	C. 120	D. 125
C©u5: TÝnh: K = , ta ®ưîc
	A. 2	B. 3	C. -1	D. 4
C©u6: Cho a lµ mét sè dư¬ng, biÓu thøc viÕt dưíi d¹ng luü thõa víi sè mò h÷u tû lµ:
	A. 	B. 	C. 	D. 
C©u7: BiÓu thøc aviÕt dưíi d¹ng luü thõa víi sè mò h÷u tû lµ:
	A. 	B. 	C. 	D. 
C©u8: BiÓu thøc (x > 0) viÕt dưíi d¹ng luü thõa víi sè mò h÷u tû lµ:
	A. 	B. 	C. 	D. 
C©u9: Cho f(x) = . Khi ®ã f(0,09) b»ng:
	A. 0,1	B. 0,2	C. 0,3	D. 0,4
C©u10: Cho f(x) = . Khi ®ã f b»ng:
	A. 1	B. 	C. 	D. 4
C©u11: Cho f(x) = . Khi ®ã f(2,7) b»ng:
	A. 2,7	B. 3,7	C. 4,7	D. 5,7
C©u12: TÝnh: K = , ta ®îc:
	A. 5	B. 6	C. 7	D. 8
C©u13: Trong c¸c phư¬ng tr×nh sau ®©y, phư¬ng tr×nh nµo cã nghiÖm?
	A. + 1 = 0	B. 	C. 	D. 
C©u14: MÖnh ®Ò nµo sau ®©y lµ ®óng?
	A. 	B. 
	C. 	D. 
C©u15: Chän mÖnh ®Ò ®óng trong c¸c mÖnh ®Ò sau:
	A. 	B. 	C. 	D. 
C©u16: Cho pa > pb. KÕt luËn nµo sau ®©y lµ ®óng?
	A. a b 	C. a + b = 0	D. a.b = 1
C©u17: Cho K = . biÓu thøc rót gän cña K lµ:
	A. x	B. 2x	C. x + 1	D. x - 1
C©u18: Rót gän biÓu thøc: , ta ®îc:
	A. 9a2b	B. -9a2b	C. 	D. KÕt qu¶ kh¸c 
C©u19: Rót gän biÓu thøc: , ta ®îc:
	A. x4(x + 1)	B. 	C. -	D. 
C©u20: Rót gän biÓu thøc: : , ta ®îc:
	A. 	B. 	C. 	D. 
C©u21: BiÓu thøc K = viÕt díi d¹ng luü thõa víi sè mò h÷u tØ lµ:
	A. 	B. 	C. 	D. 
C©u22: Rót gän biÓu thøc K = ta ®îc:
	A. x2 + 1	B. x2 + x + 1	C. x2 - x + 1	D. x2 - 1
C©u23: NÕu th× gi¸ trÞ cña a lµ:
	A. 3	B. 2	C. 1	D. 0
C©u24: Cho . MÖnh ®Ò nµo sau ®©y lµ ®óng?
	A. -3 3	C. a < 3	D. a Î R
C©u25: Trôc c¨n thøc ë mÉu biÓu thøc ta ®îc:
	A. 	B. 	C. 	D. 
C©u26: Rót gän biÓu thøc (a > 0), ta ®îc:
	A. a	B. 2a	C. 3a	D. 4a
C©u27: Rót gän biÓu thøc (b > 0), ta ®îc:
	A. b	B. b2	C. b3	D. b4
C©u28: Rót gän biÓu thøc (x > 0), ta ®îc:
	A. 	B. 	C. 	D. 
C©u29: Cho . Khi ®o biÓu thøc K = cã gi¸ trÞ b»ng:
	A. 	B. 	C. 	D. 2
C©u30: Cho biÓu thøc A = . NÕu a = vµ b = th× gi¸ trÞ cña A lµ:
	A. 1	B. 2	C. 3	D. 4
Bài 2: Cho biểu thức 
Câu 1: Khi th× giá trị của B là:
Câu 2: Khi th× giá trị của B2 là:
Câu 3: Biểu thức B được rút gọn thành:
Câu 4: Biểu thức B được rút gọn thành:
	 D. đáp án khác
Câu 5: Xác định m để biểu thức K không phụ thuộc vào giá trị của x với 
	K = B+
Câu 6: Đặt th× B trở thành:
	D. đán án khác
Câu 7: Đặt th× B trở thành:
	D. đán án khác
Câu 8 : Đặt th× B trở thành:
Câu 9: Cho x thỏa măn . Khi đó giá trị của B là:
Câu 10: Xác định x biết B = 2
Câu 11: Xác định x thỏa măn 
Câu 12: Giá trị lớn nhất của B với 	
Câu 13: Giá trị bé nhất của M với với 	
Câu 14: Đặt . Xác định t biết rằng B +1=0.
Câu 15: Có bao nhiêu giá trị x nguyên thỏa măn 
2 giá trị	B. 3 giá trị	C. 4 giá trị	D. 5 giá trị
BÀI TẬP HỖ TRỢ
Rút gọn các biểu thức sau:
TRẮC NGHIỆM TRỰC TIẾP
C©u1: Cho a > 0 vµ a ¹ 1. T×m mÖnh ®Ò ®óng trong c¸c mÖnh ®Ò sau: 
	A. cã nghÜa víi "x 	B. loga1 = a vµ logaa = 0
	C. logaxy = logax.logay	D. (x > 0,n ¹ 0)
C©u2: Cho a > 0 vµ a ¹ 1, x vµ y lµ hai sè d¬ng. T×m mÖnh ®Ò ®óng trong c¸c mÖnh ®Ò sau: 
	A. 	B. 
	C. 	D. 
C©u3: b»ng:
	A. 	B. 	C. 	D. 2
C©u4: (a > 0, a ¹ 1) b»ng:
	A. -	B. 	C. 	D. 4
C©u5: b»ng:
	A. 	B. 	C. -	D. 3
C©u6: b»ng:
	A. 4	B. 3	C. 2	D. 5
C©u7: b»ng:
	A. 3	B. 	C. 	D. 2
C©u8: b»ng:
	A. 2	B. 3	C. 4	D. 5
C©u9: b»ng:
	A. 200	B. 400	C. 1000	D. 1200
C©u10: b»ng:
	A. 4900	B. 4200	C. 4000	D. 3800
C©u11: b»ng:
	A. 25	B. 45	C. 50	D. 75
C©u12: (a > 0, a ¹ 1, b > 0) b»ng:
	A. 	B. 	C. 	D. 
C©u13: NÕu th× x b»ng:
	A. 2	B. 3	C. 4	D. 5
C©u14: NÕu th× x b»ng:
	A. 	B. 	C. 4	D. 5
C©u15: b»ng:
	A. 2	B. 3	C. 4	D. 5
C©u16: NÕu (a > 0, a ¹ 1) th× x b»ng:
	A. 	B. 	C. 	D. 3
C©u17: NÕu (a > 0, a ¹ 1) th× x b»ng:
	A. 	B. 	C. 8	D. 16
C©u18: NÕu (a, b > 0) th× x b»ng:
	A. 	B. 	C. 5a + 4b	D. 4a + 5b
C©u19: NÕu (a, b > 0) th× x b»ng:
	A. 	B. 	C. 	D. 
C©u20: Cho lg2 = a. TÝnh lg25 theo a?
	A. 2 + a	B. 2(2 + 3a)	C. 2(1 - a)	D. 3(5 - 2a)
C©u21: Cho lg5 = a. TÝnh theo a?
	A. 2 + 5a	B. 1 - 6a	C. 4 - 3a	D. 6(a - 1)
C©u22: Cho lg2 = a. TÝnh lgtheo a?
	A. 3 - 5a	B. 2(a + 5)	C. 4(1 + a)	D. 6 + 7a
C©u23: Cho . Khi ®ã tÝnh theo a lµ:
	A. 3a + 2	B. 	C. 2(5a + 4)	D. 6a - 2
C©u24: Cho . Khi ®ã log318 tÝnh theo a lµ:
	A. 	B. 	C. 2a + 3	D. 2 - 3a
C©u25: Cho log. Khi ®ã tÝnh theo a vµ b lµ:
	A. 	B. 	C. a + b	D. 
C©u26: Gi¶ sö ta cã hÖ thøc a2 + b2 = 7ab (a, b > 0). HÖ thøc nµo sau ®©y lµ ®óng?
	A. 	B. 
	C. 	D. 4
C©u27: b»ng:
	A. 8	B. 9	C. 7	D. 12
C©u28: Víi gi¸ trÞ nµo cña x th× biÓu thøc cã nghÜa?
	A. 0 2	C. -1 < x < 1	D. x < 3
C©u29: TËp hîp c¸c gi¸ trÞ cña x ®Ó biÓu thøc cã nghÜa lµ:
	A. (0; 1)	B. (1; +¥)	C. (-1; 0) È (2; +¥)	D. (0; 2) È (4; +¥)
C©u30: b»ng:
	A. 4	B. 3	C. 2	D. 1
PHẦN III: PHƯƠNG TR̀NH – BẤT PHƯƠNG TR̀NH – HỆ PHƯƠNG TR̀NH
Bài 1: Cho phương tŕnh 
Câu 1: Nếu đặt t = 2x với t > 0 th́ phương tŕnh tương đương với phương tŕnh nào:
t2 +3t -2 = 0	B. t2 -3t +2 = 0	C. t2 + 3t +2 = 0	D. t2 -3t - 2 = 0
Câu 2: Nếu thỏa măn t = 2x và t > 1. Th́ giá trị của biểu thức 2017t là:
Câu 3: Số nghiệm của phương tŕnh trên là:
Câu 4: Tập nghiệm của phương tŕnh là:
Câu 5: Phương tŕnh nên tương đương với phương tŕnh nào dưới đây:
“ 2 phương tŕnh tương đương là 2 phương tŕnh cùng tập nghiệm nhé. Đáp án A”
Câu 6: Phương tŕnh trên không tương đương với phương tŕnh nào dưới đây
Bài 2: Cho phương tŕnh 
Câu 1: Với giá trị nào của m th́ x = -2 là một nghiệm của phương tŕnh
Câu 2: Với giá trị nào của m th́ x = 1 không phải là 1 nghiệm của phương tŕnh
Câu 3: Phương tŕnh có mấy nghiệm với m = 5 / 2
BÀI TẬP TRẮC NGHIỆM TRỰC TIẾP
Ph¬ng tr×nh mò vµ ph¬ng tr×nh l«garÝt
C©u1: Ph¬ng tr×nh cã nghiÖm lµ:
	A. x = 	B. x = 	C. 3	D. 5
C©u2: TËp nghiÖm cña ph¬ng tr×nh: lµ:
	A. 	B. {2; 4}	C. 	D. 
C©u3: Ph¬ng tr×nh cã nghiÖm lµ:
	A. 	B. 	C. 	D. 2
C©u4: Ph¬ng tr×nh cã nghiÖm lµ:
	A. 3	B. 4	C. 5	D. 6
C©u5: Ph¬ng tr×nh: cã nghiÖm lµ:
	A. 2	B. 3	C. 4	D. 5
C©u6: Ph¬ng tr×nh: cã nghiÖm lµ:
	A. -3	B. 2	C. 3	D. 5
C©u7: TËp nghiÖm cña ph¬ng tr×nh: lµ:
	A. 	B. 	C. 	D. 
C©u8: Ph¬ng tr×nh: cã nghiÖm lµ:
	A. 1	B. 2	C. 3	D. 4
C©u9: Ph¬ng tr×nh: cã nghiÖm lµ: 
	A. 3	B. 2	C. 1	D. 0
C©u10: Ph¬ng tr×nh: cã nghiÖm lµ:
	A. 1	B. 2	C. 3	D. 4
C©u11: X¸c ®Þnh m ®Ó ph¬ng tr×nh: cã hai nghiÖm ph©n biÖt? §¸p ¸n lµ:
	A. m 2	D. m Î 
C©u12: Ph¬ng tr×nh: cã nghiÖm lµ:
	A. 7	B. 8	C. 9	D. 10
C©u13: Ph¬ng tr×nh: = 3lgx cã nghiÖm lµ:
	A. 1	B. 2	C. 3	D. 4
C©u14: Ph¬ng tr×nh: = 0 cã mÊy nghiÖm?
	A. 0	B. 1	C. 2	D. 3
C©u15: Ph¬ng tr×nh: 
	A. 0	B. 1	C. 2	D. 3
C©u16: Ph¬ng tr×nh: cã nghiÖm lµ:
	A. 24	B. 36	C. 45	D. 64
C©u17: Ph¬ng tr×nh: cã tËp nghiÖm lµ:
	A. 	B. 	C. 	D. 
C©u18: Ph¬ng tr×nh: cã tËp nghiÖm lµ:
	A. 	B. 	C. 	D. 
C©u19: Ph¬ng tr×nh: = 1 cã tËp nghiÖm lµ:
	A. 	B. 	C. 	D. 
C©u20: Ph¬ng tr×nh: cã tËp nghiÖm lµ:
	A. 	B. 	C. 	D. 
C©u21: Ph¬ng tr×nh: cã tËp nghiÖm lµ:
	A. 	B. 	C. 	D. 
C©u22: Ph¬ng tr×nh: cã tËp nghiÖm lµ:
	A. 	B. 	C. 	D. 
HÖ ph¬ng tr×nh mò vµ l«garÝt
C©u1: HÖ ph¬ng tr×nh: víi x ≥ y cã mÊy nghiÖm?
	A. 1	B. 2	C. 3	D. 0
C©u2: HÖ ph¬ng tr×nh: cã nghiÖm lµ:
	A. 	B. 	C. 	D. 
C©u3: HÖ ph¬ng tr×nh: cã mÊy nghiÖm?
	A. 0	B. 1	C. 2	D. 3
C©u4: HÖ ph¬ng tr×nh: cã nghiÖm lµ:
	A. 	B. 	C. 	D. 
C©u5: HÖ ph¬ng tr×nh: víi x ≥ y cã nghiÖm lµ?
	A. 	B. 	C. 	D. KÕt qu¶ kh¸c 
C©u6: HÖ ph¬ng tr×nh: víi x ≥ y cã nghiÖm lµ?
	A. 	B. 	C. 	D. KÕt qu¶ kh¸c
C©u7: HÖ ph¬ng tr×nh: víi x ≥ y cã nghiÖm lµ:
	A. 	B. 	C. 	D. KÕt qu¶ kh¸c
C©u8: HÖ ph¬ng tr×nh: cã nghiÖm lµ:
	A. 	B. 	C. 	D. 
C©u9: HÖ ph¬ng tr×nh: cã nghiÖm lµ:
	A. 	B. 	C. 	D. 
C©u10: HÖ ph¬ng tr×nh: cã nghiÖm lµ
	A. 	B. 	C. 	D. KÕt qu¶ kh¸c
BÊt ph¬ng tr×nh mò vµ l«garÝt
C©u1: TËp nghiÖm cña bÊt ph¬ng tr×nh: lµ:
	A. 	B. 	C. 	D. 
C©u2: BÊt ph¬ng tr×nh: cã tËp nghiÖm lµ:
	A. 	B. 	C. 	D. KÕt qu¶ kh¸c 
C©u3: BÊt ph¬ng tr×nh: cã tËp nghiÖm lµ:
	A. 	B. 	C. (0; 1)	D. 
C©u4: BÊt ph¬ng tr×nh: cã tËp nghiÖm lµ:
	A. 	B. 	C. 	D. 
C©u5: BÊt ph¬ng tr×nh: cã tËp nghiÖm lµ:
	A. 	B. 	C. 	D. KÕt qu¶ kh¸c 
C©u6: BÊt ph¬ng tr×nh: 2x > 3x cã tËp nghiÖm lµ:
	A. 	B. 	C. 	D. 
C©u7: HÖ bÊt ph¬ng tr×nh: cã tËp nghiÖm lµ:
	A. [2; +¥)	B. [-2; 2]	C. (-¥; 1]	D. [2; 5]
C©u8: BÊt ph¬ng tr×nh: cã tËp nghiÖm lµ:
	A. (0; +¥)	B. 	C. 	D. 
C©u9: BÊt ph¬ng tr×nh: cã tËp nghiÖm lµ:
	A. 	B. 	C. (-1; 2)	D. (-¥; 1)