Cách giải 12 bài toán tỉ lệ thức

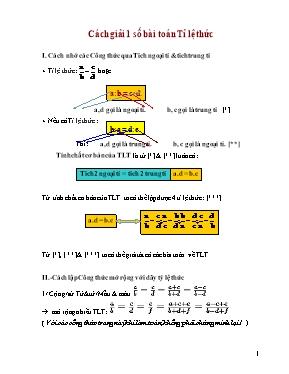
Cách giải 1 số bài toán Tỉ lệ thức 
I. Cách nhớ các Công thức qua Tich ngoại tỉ &tich trung tỉ
+ Tỉ lệ thức : hoặc 
a:b = c:d.
 a, d gọi là ngoại tỉ. b, c gọi là trung tỉ. [*]
b:a = d:c
+ Nếu có Tỉ lệ thức : 
Thì: a, d gọi là trung tỉ. b, c gọi là ngoại tỉ. [**]
 Tính chất cơ bản của TLT là từ [*] & [**] luôn có: 
Tich 2 ngoại tỉ = tich 2 trung tỉ
a.d = b.c
Từ tính chất cơ bản của TLT ta có thể lập được 4 tỉ lệ thức : [***]
a.d = b.c
Từ [*], [ **] & [***] ta có thể giải tât cả các bài toán về TLT
II.-Cách lập Công thức mở rộng với dãy tỷ lệ thức
1/ Cộng/trừ Tử&tử /Mẫu & mâu 
à mở rộng nhiều TLT: 
( Với các công thức trang này khi làm toán, không phải chứng minh lại ! )
III.- Một số phương pháp giải toán TLT
1/ Qua Tich 2 ngoại tỉ = tich 2 trung tỉ
1.1/ Lập các tỉ lệ thức từ đẳng thức hoặc từ tỉ lệ thức gốc
Bài 1: Lập tất cả các tỉ lệ thức có thể được từ các đẳng thức sau:                          
a) 6.63 = 9. 42 b) 0,24.1,61 = 0,84. 0,46
Lời giải:
a) Các tỉ lệ thức có được từ đẳng thức 6.63 = 9. 42
b) Các tỉ lệ thức có được từ đẳng thức:  0,24.1,61 = 0,84. 0,46
Bài 2:  Lập tất cả các tỉ lệ thức có thể được từ tỉ lệ thức sau                                      
Lời giải:
Từ tỉ lệ thức   ta có được 3 tỉ lệ thức sau:
1.2/ Qua Tich ngoại tỉ trung tỉ, tìm giá trị chưa biết trong các tỉ lệ thức
Bài 3: Tìm x trong các tỉ lệ thức sau:
 a) b) 
c) d) 
Giải: 
Đổi các tỉ lệ thức àTich ngoại tỉ trung tỉ à tinh x
a,/ 4,125 : 0,2 = x : 0,3
 20,625 = x: 0,3 Þ x= 6.1875
b/ 0,5:2,6 = 0,01x:4
 0,192=0,01x : 4 Þ X= 76,8
c/, (3,39.2,5):19,75=x: 5,83
 8.475:19,75=x:5,83 Þ x = 2,50107
d/, 0.25: 1,11=31x : (- 0,139)
 0,225=31x : (0,139) Þ x = 0,001
Bài 4: Tìm x trong các tỉ lệ thức 
 e) ;	 f) ;
Giải:
e/ , (x – 1).7= (x+5).6
 7x – 7 = 6x + 30 Þ x = 37
 g/, x2 . 25 = 6 . 24 = 144
 x2 . 52 = 122 Þ (5x)2 =(12)2Þx = ±2,4
2.- Phương pháp Tìm/đặt hệ số
2.1/ Với bài toán có x ± y àTìm hệ số theo x ± y
Bài 5  Tìm hai số x va y, biết  và x + y = 16
Lời giải:
Theo tính chất của dãy tỉ số bằng nhau ta có:
Hệ số = 2 à Do đó
 ; è ĐS: x=6, y =10
Bài 6: Tìm hai số x và y, biết x:2 = y : (-5)  và x - y = -3                                     
Lời giải:  
Theo tính chất của dãy tỉ số bằng nhau ta có:
Hệ số = - 1 à Do đó:
 ; èx = -2 và y = 5
Bài 7  
Tìm diện tích của một hình chữ nhật biết rằng tỉ số giữa hai cạnh của nó bằng 2/5 và chu vi bằng 28m
Lời giải:
Gọi x (m) là chiều rộng, y (m) là chiều dài ( x, y >0)
Tỉ số giữa hai cạnh là  nên suy ra  hay 
Theo tính chất của dãy tỉ số bằng nhau, ta có:
Hệ số = 2 à Do đó
: ; 
Vậy diện tích hình chữ nhật là: S = 10.4 = 40  (m2)
Bài 8 
Hai lớp 7A và 7B đi lao động trồng cây. Biết rằng tỉ số giữa cây trồng được của lớp 7A và lớp 7B là 0,8 và lớp 7B trồng nhiều hơn lớp 7A là 20 cây. Tính số cây mỗi lớp đã trồng?
Giải:
Gọi x, y lần lượt là số cây trồng được của lớp 7A, 7B. 
Theo đề bài ta có:
  và y - x = 20
Theo tính chất của dãy tỉ số bằng nhau ta có:
Hệ số = 2 à Do đó
; 
Vậy số cây của lớp 7A là 80, của lớp 7B là 100
2.2/ Với bài toán có x . y à đặt hệ số phụ k
Bài 9 
Tìm chu vi của một hình chữ nhật biết rằng tỉ số giữa hai cạnh của nó bằng 2/5 và diện tích bằng 90 m2
Lời giải:
 Gọi x (m) là chiều rộng, y (m) là chiều dài ( x, y >0)
 Tỉ số giữa hai cạnh là  nên suy ra   hay  
k = 
 đặt hệ số phụ 
 [*]
 Do đó: x = 2k và y = 5k ; Thay các giá trị này vào x.y = 90 (điều bài toán cho)
 Tính được 90 = 10 k2 à k 2 = 9 à k = 3
Thay k = 3 váo [*] à x = 6; y = 15 è chu vi của một hình chữ nhật= 42 (m)
2.3/ Với bài toán chứng minh à đặt hệ số phụ k
Bài 10 ( Bài toán chứng minh)
 Cho chứng minh rằng 
Lời giải:
 Đặt à a = bk; c = dk. Tính theo k ta có
 (ĐPCM)
3/- Phương pháp đặt “Số gia” vào 2 về Trung tỉ ngoại tỉ
Bài 11 Tổng quát
Cho chứng minh rằng 
Giải
 - Thêm “Số gia” n vào đảng thức ab = cd à n + ab = n + cd [1] 
 - Biết a/a = c/c =1 à nhân vào từng vế của [1] có 
Bài 12 Cho chứng minh rằng 
 Giải so với Bài 11 bài này có n=3 và biến thể ở mẫu số
 Từ ad = bc, ta thêm vào 2 vế 3ac được: 
 3ac + ad = 3ac + bc à a(3ac + d) = c(3a + b) à (ĐPCM)