Các công thức chuyên sâu thi THPT quốc gia môn Vật lí - Nguyễn Văn Dân

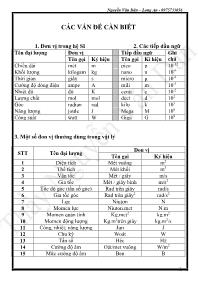
Nguyễn Văn Dân – Long An - 0975733056 
 1 
CÁC VẤN ĐẾ CẦN BIẾT 
 1. Đơn vị trong hệ SI 2. Các tiếp đầu ngữ 
Tên đại lượng Đơn vị Tiếp đầu ngữ Ghi 
chú Tên gọi Ký hiệu Tên gọi Kí hiệu 
Chiều dài mét m pico p 10-12 
Khối lượng kilogam kg nano n 10-9 
Thời gian giây s micro μ 10-6 
Cường độ dòng điện ampe A mili m 10-3 
Nhiệt độ độ K centi c 10-2 
Lượng chất mol mol deci d 102 
Góc radian rad kilo k 103 
Năng lượng joule J Mega M 106 
Công suất watt W Giga G 109 
3. Một số đon vị thường dùng trong vật lý 
STT Tên đại lượng 
Đon vị 
Tên gọi Ký hiệu 
1 Diện tích Mét vuông m2 
2 Thể tích Mét khối m3 
3 Vận tốc Mét / giây m/s 
4 Gia tốc Mét / giây bình m/s2 
5 Tốc độ góc (tần số góc) Rad trên giây rad/s 
6 Gia tốc góc Rad trên giây2 rad/s2 
7 Lực Niutơn N 
8 Momen lực Niuton.met N.m 
9 Momen quán tính Kg.met2 kg.m2 
10 Momen động lượng Kg.m2trên giây kg.m2/s 
11 Công, nhiệt; năng lượng Jun J 
12 Chu kỳ Woát W 
13 Tần số Héc Hz 
14 Cường độ âm Oát/met vuông W/m2 
15 Mức cường độ âm Ben B 
Nguyễn Văn Dân – Long An - 0975733056 
 2 
4. Kiến thức toán cơ bản: 
a. Đạo hàm của một số hàm cơ bản sử dụng trong Vật Lí: 
Hàm số Đạo hàm 
y = sinx y’ = cosx 
y = cosx y’ = - sinx 
b. Các công thức lượng giác cơ bản: 
2sin2a = 1 – cos2a - cos = cos( + ) - sina = cos(a + 
2

) 
2cos2a = 1 + cos2a sina = cos(a - 
2

) 
sina + cosa = )
4
sin(2

a - cosa = cos(a +  ) 
sina - cosa = )
4
sin(2

a cosa - sina = )
4
sin(2

a 
3
sin3 3sin 4sina a a  
3
cos3 4cos 3cosa a a  
c. Giải phương trình lượng giác cơ bản: 
sin 








2
2
sin
ka
ka
a
 cos  2cos kaa  
d. Bất đẳng thức Cô-si: baba .2 ; (a, b  0, dấu “=” khi a = b) 
e. Định lý Viet: yx
a
c
Pyx
a
b
Syx
,
.









là nghiệm của X2 – SX + P = 0 
 Chú ý: y = ax2 + bx + c; để ymin thì x = 
a
b
2

; 
 Đổi x0 ra rad: 
180
0x 
Nguyễn Văn Dân – Long An - 0975733056 
 3 
 g. Các giá trị gần đúng: 
 + Số 𝛑 2 10; 314100 ; 0,318 

1
; 0,636 

2
; 0,159 
2
1
; 
 + Nếu x ≪ 1 thì (1 ± x)x = 1 ± nx; 1
1 2
2
1 x
1 x x
1 x

 

; 
x
(1 x) 1
2
   ; 
1
1 x
1 x


; 2121 1)1)(1(   
 + Nếu 𝛂 < 100 (𝛂 nhỏ): tan𝛂 ≈ sin𝛂 ≈ 𝛂rad ; cosα = 1 - 
2
2

 h. Công thức hình học 
 * Trong một tam giác ABC có ba cạnh là a, b, c (đối diện 3 góc A; B;C ) 
ta có : 
 + a2 = b2 + c2 + 2 a.b.cosA ; (tương tự cho các cạnh còn lại) 
 + 
a b c
sinA sinB sinC
  
 * Hình cầu 
 + Diện tích mặt cầu S = 4𝛑R2 
 + Thể tích hình cầu V =  3
4
R
3
---------- 
Nguyễn Văn Dân – Long An - 0975733056 
 4 
Chương I: DAO ĐỘNG CƠ HỌC 
I - ĐẠI CƯƠNG VỀ DAO ĐỘNG ĐIỀU HOÀ 
 T: chu kỳ; f: tần số; x: li độ; v: vận tốc; a: gia tốc; g: gia tốc trọng 
trường; A: biên độ dao động; (t + ): pha dao động; : pha ban đầu; : tốc 
độ góc; 
1. Phương trình dao động 
    tAcosx 
 - Chu kỳ: 

2
T (s) - Tần số: 


2
1

T
f (Hz) 
 - NÕu vËt thùc hiÖn ®-îc N dao ®éng trong thêi 
gian t th×: 
 à

 

t N
T v f
N t
. 
2. Phương trình vận tốc 
    tAxv sin' 
 - x = 0 (VTCB) thì vận tốc cực đại: Av max 
 - x  A (biên) thì 0v  
3. Phương trình gia tốc 
  2 2' cosa v A t x         
 - x = A thì 
2
maxa A 
 - x = 0 thì 0a  
 Ghi chú: Liên hệ về pha:  v sớm pha 
2

 hơn x; 
  a sớm pha 
2

 hơn v; 
  a ngược pha với x. 
4. Hệ thức độc lập thời gian giữa x, v và a 
 - Giữa x và v: 
2
2
22

v
xA  
 - Giữa v và a:  
2
22 2
2max
a
v A v

   
Nguyễn Văn Dân – Long An - 0975733056 
 5 
 - Giữa a và x: 
2
a x  
5. Các liên hệ khác 
 - Tốc độ góc: 
max
max
v
a
 
 - Tính biên độ 
2
222
2
2
2
max
2
max
2
maxmax 2
42 


avv
x
k
W
a
vav
n
SL
A

 
6. Tìm pha ban đầu 
2
A 2
2
A
3
2
A
A O A
2

A
 2
2
A 3
2
A
v < 0 
 φ = + π/2 
 v < 0 
φ = + π/4 
v < 0 
φ = + π/6 
v = 0 
φ = 0 
v < 0 
φ = + π/3 
v > 0 
φ = - π/6 
v < 0 
φ = + 2π/3 
v > 0 
φ = - π/2 
v > 0 
φ = - π/3 
v > 0 
φ = - π/4 
v < 0 
φ = + 3π/4 
v < 0 
φ = + 5π/6 
v > 0 
φ = -5π/6 
v > 0 
φ = - 3π/4 
v > 0 
φ = - 2π/3 
v = 0 
φ = ± π 
Nguyễn Văn Dân – Long An - 0975733056 
 6 
6. Thời gian ngắn nhất để vật đi từ: 
 + x1 đến x2 (giả sử 21 xx  ): 



 12 


t với








A
x
A
x
2
2
1
1
cos
cos


    21,0 . 
 + x1 đến x2 (giả sử 1 2x x ): 



 12 


t với 








A
x
A
x
2
2
1
1
cos
cos


 1 2, 0     
7. Vận tốc trung bình - tốc độ trung bình 
 - Tốc độ trung bình v 
S
t
 
 - Độ dời ∆x trong n chu kỳ bằng 0; 
 quãng đường vật đi được trong n chu kỳ bằng nAS 4 . 
 - Vận tốc trung bình 
x
v
t



. 
8. Tính quãng đường vật đi được trong thời gian t 
 + Sơ đồ 1: 
 x 
 -A  A
2
 0(VTCB) A
2 
A 2
2 
 A 3
2
 +A 
 T/4 T/12 T/6 
 T/8 T/8 
 T/6 T/12 
 + Sơ đồ 2: 
 x 
 0 (VTCB) 
A
2 
A 2
2 
 A 3
2
 +A 
 T/12 T/24 T/24 T/12 
Nguyễn Văn Dân – Long An - 0975733056 
 7 
* Công thức giải nhanh tìm quãng đường đi (dùng máy tính) 
 x1 (bất kì) x 
 0 
 +A 
 t1 = 
1
x1
arsin
A


 t1 = 
1
x1
ar cos
A


* Phương pháp chung tìm quãng đường đi trong khoảng thời gian nào đó 
ta cần xác định: 
 - Vị trí vật lúc t = 0 và chiều chuyển động của vật lúc đó; 
 - Chia thời gian ∆t thành các khoảng nhỏ: nT; nT/2; nT/4; nT/8; nT/6; 
T/12  với n là số nguyên; 
 - Tìm quãng đường s1; s2; s3;  tương úng với các quãng thời gian nêu 
trên và cộng lại 
  Tính quãng đường ngắn nhất và bé nhất vật đi được trong khoảng thời 
gian t với 
2
0
T
t  
Nguyên tắc: 
 + Vật đi được quãng đường -A - x0 O x0 +A 
dài nhất khi li độ điểm đầu và điểm 
cuối có giá trị đối nhau smax 
 Quãng đường dài nhất: max 2 sin
2
t
S A

 
 + Vật đi được quãng đường -A - x0 O x0 +A 
ngắn nhất khi li độ điểm đầu và điểm 
cuối có giá trị bằng nhau 
 smin Smin 
 Quãng đường ngắn nhất: min 2 1 cos
2
t
S A
 
  
 
Nguyễn Văn Dân – Long An - 0975733056 
 8 
 Trường hợp 
2
T
t  thì ta tách t
T
nt 
2
 * 0
2
T
n N và t
 
    
 
: 
 + Quãng đường lớn nhất: max 2 2 sin
2
t
S nA A

  
 + Quãng đường nhỏ nhất: min 2 2 1 cos
2
t
S nA A
 
   
 
 + Tốc độ trung bình lớn nhất trong thời gian t: maxaxtbm
S
v
t
 
 + Tốc độ trung bình nhỏ nhất trong thời gian t: minmintb
S
v
t
 
+ Sơ đồ quan hệ giữa li độ và vận tốc 
 maxv v
max
3
v v
2 
max
2
v v
2 
max
v
v
2

v 0 
 x 
 0 (VTCB) 
A
2 
A 2
2 
 A 3
2
 +A 
II - CON LẮC LÒ XO 
l : độ biến dạng của lò xo khi vật cân bằng; 
 k: độ cứng của lò xo (N/m); 0l : chiều dài tự nhiên của lò xo 
1. Công thức cơ bản 
 - Tần số góc: 
k g
m l
  

; 
 + Con lắc lò xo treo thẳng đứng: 
2
mg g
l
k 
   ; 
 + Đặt con lắc trên mặt phẳng nghiêng góc  không ma sát: 
Nguyễn Văn Dân – Long An - 0975733056 
 9 
sinmg
l
k

  
 - áp dụng công thức về chu kỳ và tần số: 
 2. Chiều dài cực đại và cực tiểu của lò xo 
 + dao động thẳng đứng: 
 
 




Alll
Alll
0max
0min
2
minmax llA

 
 + dao động phương ngang: 
min 0
max 0
A
l A
l l
l
  

 
3.Ghép lò xo. 
 - Ghép nối tiếp: 
nkkkk
1
...
111
21
 
 - Ghép song song: nkkkk  ...21 
 - Gọi T1 và T2 là chu kỳ khi treo m vào lần lượt 2 lò xo k1 và k2 thì: 
 + Khi ghép k1 nối tiếp k2: 







2
2
2
1
2
2
2
2
1
111
fff
TTT
 + Khi ghép k1 song song k2: 







2
2
2
1
2
2
2
2
1
111
TTT
fff
 - Gọi T1 và T2 là chu kỳ khi treo m1 và m2 lần lượt vào lò xo k thì: 
 + Khi treo vật 21 mmm  thì: 
2
2
2
1 TTT  
 + Khi treo vật 21 mmm  thì: 
2
2
2
1 TTT   21 mm  
4. Cắt lò xo 
 - Cắt lò xo có độ cứng k, chiều dài 
0l thành nhiều đoạn có 
2
2 2
1 1 1
2 2
m l
T
k g
k g
f
T m l

 

 
 
  



   
Nguyễn Văn Dân – Long An - 0975733056 
 10 
chiều dài nlll ...,,, 21 có độ cứng tương ứng nkkk ...,,, 21 liên hệ nhau theo 
hệ thức: 
 nnlklklkkl  ...22110 . 
- Nếu cắt lũ xo thành n đoạn bằng nhau (cỏc lũ xo cú cùng độ cứng k’): 
 nkk ' hay: 







nff
n
T
T
'
'
5. Lực đàn hồi - lực hồi phục 
Nội 
dung 
Lực hồi phuc 
Lực đàn hồi 
Lò xo nằm 
ngang 
Lò xo thẳng đứng 
A ≥ ∆l A < ∆l 
Gốc tại 
Vị trí cân bằng Vị trí lò xo chưa biến dạng 
Bản chất 
 hp dh
F P F  Fđh = k . (độ biến dạng) 
Ý nghĩa 
và tác 
dụng 
- Gây ra chuyển động 
của vật 
- Giúp vật trở về 
VTCB 
- Giúp lò xo phục hồi hình dạng cũ 
- Còn gọi là lực kéo (hay lực đẩy) của lò 
xo lên vật (hoặc điểm treo) 
Cực đại 
Fmax = kA 
Fmax = kA Fmax = k(∆l + A) 
Cực tiểu 
Fmin = 0 
Fmin = 0 Fmin = 0 
Fmin = k(∆l – 
A) 
Vị trí 
bất kì 
F = k x F = k x F = k(∆l + x) 
III - CON LẮC ĐƠN 
1. Công thức cơ bản 
Dưới đây là bảng so sánh các đặc trưng chính của hai hệ dao động. 
Hệ dao động Con lắc lò xo Con lắc đơn 
Cấu trúc 
Hòn bi m gắn vào lò xo (k). Hòn bi (m) treo vào đầu sợi 
dây (l). 
Nguyễn Văn Dân – Long An - 0975733056 
 11 
VTCB 
- Con lắc lò xo ngang: lò 
xo không giãn 
- Con lắc lò xo thẳng đứng 
nó dãn 
k
mg
l  
Dây treo thẳng đứng 
Lực tác dụng 
Lực đàn hồi của lò xo: 
F = - kx 
x là li độ dài 
Trọng lực của hòn bi và lực 
căng của dây treo: 
s
l
g
mF  s là li độ cung 
Tần số góc 
m
k
 = 
g
l
l
g
 
Phương trình 
dao động. 
x = Acos(ωt + φ) s = s0cos(ωt + φ) 
Hoặc α = α0cos(ωt + φ) 
Cơ năng 
2 2 21 1
2 2
W kA m A  0
(1 cos )W mgl   
2
0s
l
g
m
2
1
 
 - Chu kỳ dao động của con lắc đơn có chiều dài l1 và l2 lần lượt là T1 và T2 
thì: 
 + Chu kỳ của con lắc có chiều dài 21 lll  : 
2
2
2
1 TTT  
 + Chu kỳ của con lắc có chiều dài 21 lll  : 
2
2
2
1 TTT   21 ll  . 
 - Liên hệ giữa li độ dài và li độ góc: s l 
 - Hệ thức độc lập thời gian của con lắc đơn: 
 a = - 2s = - 2αl; 
2 2 2
0 ( )
v
S s

  
2
2 2
0
v
gl
   
2. Lực hồi phục 
2
sin
s
F mg mg mg m s
l
          
3. Vận tốc - lực căng 
 + Khi con lắc ở vị trí li độ góc  vận tốc và lực căng tương ứng của vật: 
Nguyễn Văn Dân – Long An - 0975733056 
 12 
 
 
0
0
2 cos cos
3cos 2cosc
v gl
T mg
 
 
  

 
Khi 0 nhỏ: 
 2 20
2 2
0
3
1
2
c
v gl
T mg
 
 
  

  
    
  
 + Khi vật ở biên: 
0
0
cos
c
v
T mg 



; khi 0 nhỏ: 
2
0
0
1
2
c
v
T mg



 
  
 
 + Khi vật qua VTCB: 
 
 
0
0
2 1 cos
3 2cosc
v gl
T mg


  

 
; khi 0 nhỏ:  
0
2
01c
v gl
T mg


 

 
4. Biến thiên chu kỳ của con lắc đơn phụ thuộc: nhiệt độ, độ sâu và độ 
cao. Thời gian nhanh chậm của đồng hồ vận hành bằng con lắc đơn 
 a.Công thức cơ bản 
 * Gọi chu kỳ ban đầu của con lắc là 0T (chu kỳ chạy đúng), Chu kỳ sau 
khi thay đổi là T (chu kỳ chạy sai). 
 0TTT  : độ biến thiên chu kỳ. 
 + 0T  đồng hồ chạy chậm lại; 
 + 0T  đồng hồ chạy nhanh lên. 
 * Thời gian nhanh chậm trong thời gian N (1 ngày đêm 
24 86400N h s  ) sẽ bằng: 
0
TN
T N
T T


   
 b. Các trường hợp thường gặp 
 Khi nhiệt độ thay đổi từ 1t đến 2t : 
0
1
2
1
2
T
t
T
N t

 

 

  

 ( 2 1t t t   ) 
Nguyễn Văn Dân – Long An - 0975733056 
 13 
 Khi đưa con lắc từ độ cao 1h đến độ cao 2h : 
0
T h
T R
h
N
R

 






( 2 1h h h   ) 
 Khi đem vật lên cao 0h  , khi đem vật xuống độ cao thấp hơn 
0h . Ban đầu vật ở mặt đất thì 01 h và hh  
 Khi đưa con lắc từ độ sâu 1h đến độ sâu 2h :
0
2
2
T h
T R
N h
R

 






( 2 1h h h   ) 
 Khi đem vật xuống sâu 012  hhh , khi đem vật lên cao hơn ban 
đầu 0h . Ban đầu vật ở mặt đất thì 01 h và hh  
 c. Các trường hợp đặc biệt 
 - Khi đưa con lắc ở mặt đất (nhiệt độ 1t ) lên độ cao h (nhiệt độ 2t ): 
0
1
2
T h
t
T R


   
 Nếu đồng hồ vẫn chạy đúng so với dưới mặt đất thì: 
0
1
0
2
T h
t
T R


    
 - Khi đưa con lắc từ trái đất lên mặt trăng (coi chiều dài l không đổi) thì: 
TĐ
MT
MT
TĐ
MT
TĐ
M
M
R
R
T
T
 
 - Khi cả l và g thay đổi một lượng rất nhỏ thì 
0 0 0
1 1
.
2 2
  
 
T l g
T l g
 - Khi cả nhiệt độ và g thay đổi một lượng rất nhỏ thì 
0 0 0
1 1
.
2 2
  
 
T l g
T l g
5. Con lắc đơn chịu tác dụng của lực phụ không đổi 
 * Lực phụ f

gặp trong nhiều bài toán là: 
Nguyễn Văn Dân – Long An - 0975733056 
 14 
 + Lực quán tính amFq

 , độ lớn: maFq  , (a là gia tốc của hệ quy 
chiếu) 
 + Lực điện trường F qE , độ lớn: EqF  , 
 q là điện tích của vật, E là cường độ điện trường nơi đặt con lắc ( /V m ) 
 + Lực đẩy Acsimet gV

AF , độ lớn: VgFA  . 
  là khối lượng riêng của môi truờng vật dao động, V là thể tích vật 
chiếm chỗ 
Chu kỳ dao động trong trường hợp này sẽ là: 
g
l
T

 2 , 
 'g là gia tốc trọng trường hiệu dụng. 
 * Tính g': 
 + Trường hợp Pf

 : 
m
f
gg ' 
  Lực quán tính: agg ' 
  Lực điện trường: 
m
Eq
gg ' 
 + Trường hợp Pf

 : 
m
f
gg ' 
  Lực quán tính: agg ' 
  Lực điện trường: 
m
Eq
gg ' 
  Lực đẩy Acsimét: 
m
Vg
gg

' 
 + Trường hợp Pf

 : 
2
2
' 






m
f
gg 
  Lực quán tính: 
22
' agg  
  Lực điện trường: 
2
2
' 






m
qE
gg 
Nguyễn Văn Dân – Long An - 0975733056 
 15 
Chú ý: + Trường hợp Pf

 thì góc lệch  của sợi dây so với phương 
thẳng đứng được tính: 
P
f
tan 
 + Khi con lắc đơn gắn trên xe và chuyển động trên mặt phẳng 
nghiêng góc  không ma sát thì VTCB mới của con lắc là sợi dây lệch 
góc   (sợi dây vuông góc với mặt phẳng nghiêng) so với phương 
thẳng đứng và chu kỳ dao động của nó là: 


cos
2'
g
l
T  
V - NĂNG LƯỢNG DAO ĐỘNG 
 -Động năng:    tAmmvWd
2222
sin
2
1
2
1
 - Thế năng:    tAmkxWt
2222
cos
2
1
2
1
 - Động năng và thế năng biến thiên tuần hoàn với chu kỳ bằng 1/2 chu kỳ 
dao động điều hoà (T’ = T/2). 
 - Khoảng thời gian giữa 2 lần động năng và thế năng bằng nhau liên tiếp là 
T/4. 
 cos 
 -A  A
2
 0 
A
2 
A 2
2 
 A 3
2
 +A 
 T/4 T/12 T/6 
 Với T/8 T/8 
 T/6 T/12 
1. Con lắc lò xo (Chọn gốc thế năng tại VTCB) 
Wđ = 3 Wt Wđmax 
Wt = 0 
Wt = 3 Wđ Wđ = Wt Wđ = 0 
Wtmax 
W = Wtmax = Wđmax = 1/2kA2 
Nguyễn Văn Dân – Long An - 0975733056 
 16 
 - Động năng: 
2
2
1
mvWđ  ; Thế năng: 
2
2
1
kxWt  
 - Cơ năng: tđ WWW 
222
2
1
2
1
AmkA  
 + Vị trí của vật khi tđ nWW  : 
1

n
A
x 
 + Vận tốc của vật lúc đt nWW  : 
11
max




n
A
n
v
v

 + Động năng khi vật ở li độ x:  22
2
1
xAkWđ  
 + Tỉ số động năng và thế năng: 
2
22
x
xA
W
W
t
đ  
 2. Con lắc đơn (Chän gèc thÕ n¨ng t¹i VTCB) 
 - Động năng: 
2
2
1
mvWđ  ; Thế năng:  cos1 mglWt 
 - Cơ năng: tđ WWW   0cos-1mgl  
  Khi góc 0 bé thì: 
21
2
tW mgl ; 
2
0
1
W mgl
2
 
 + Vị trí của vật khi 
 tđ nWW  : 
1
0


n
S
S và 
1
0


n

 
 + Vận tốc của vật lúc 
 đt nWW  : 
1
max


n
v
v
1
0


n
S
 + Động năng của vật khi nó ở li độ  :
    2202220
2
1
2
1
SSmmglWđ   
 + Tỉ số động năng và thế năng: 
2
22
0
2
22
0
S
SS
W
W
t
đ 




Nguyễn Văn Dân – Long An - 0975733056 
 17 
VI - TỔNG HỢP DAO ĐỘNG 
1. Phương pháp giản ®å Frexnel 
- Bài toán: Tổng hợp 2 dao động điều hoà cùng phương: 
 
 
1 1 1
2 2 2
cos
cos
x A t
x A t
 
 
 

 
  cosx A t    
 Với 
 









2211
2211
2121
2
2
2
1
coscos
sinsin
tan
cos2




AA
AA
AAAAA
- Nếu biết một dao động thành phần  111 cos   tAx và dao động 
tổng hợp    tAx cos thì dao động thành phần còn lại là 
 222 cos   tAx được xác định: 
 









11
11
2
11
2
1
22
2
coscos
sinsin
tan
cos2




AA
AA
AAAAA
(với 21   ) 
- Nếu 2 dao động thành phần vuông pha thì: 
2
2
2
1 AAA  
 2. Tìm dao động tổng hợp xác định A và  bằng cách dùng máy 
tính thực hiện phép cộng: 
 + Với máy FX570ES: Bấm chọn MODE 2 màn hình xuất hiện chữ: 
CMPLX. 
 -Chọn đơn vị đo góc là độ bấm: SHIFT MODE 3 màn hình hiển thị chữ D 
 (hoặc Chọn đơn vị góc là Rad bấm: SHIFT MODE 4 màn hình hiển thị 
chữ R ) 
 -Nhập A1 SHIFT (-) φ1, + Nhập A2 SHIFT (-) φ2 nhấn = hiển thị kết 
quả. 
 (Nếu hiển thị số phức dạng: a+bi thì bấm SHIFT 2 3 = hiển thị kết 
quả: A) 
Nguyễn Văn Dân – Long An - 0975733056 
 18 
 + Với máy FX570MS : Bấm chọn MODE 2 màn hình xuất hiện chữ: 
CMPLX. 
Nhập A1 SHIFT (-) φ1 + Nhập A2 SHIFT (-) φ2 = 
 Sau đó bấm SHIFT + = hiển thị kết quả là: A. SHIFT = hiển thị kết 
quả là: φ 
 + Lưu ý Chế độ hiển thị màn hình kết quả: 
Sau khi nhập ta ấn dấu = có thể hiển thị kết quả dưới dạng số vô tỉ, muốn 
kết quả dưới dạng thập phân ta ấn SHIFT = (hoặc dùng phím SD ) 
để chuyển đổi kết quả Hiển thị. 
VII - DAO ĐỘNG TẮT DẦN 
- Tìm tổng quãng đường S mà vật đi được cho đến khi dừng lại: 
 SFkA C
2
2
1
- Độ giảm biên độ sau 1 dao động: 
2
4 CFA
m
  
k
FC4 , CF là lực cản 
 Nếu Fc là lực ma sát thì : 
k
N
A
4
 
- Số dao động thực hiện được: 
CF
Ak
A
A
N
4
.
' 11 

 
 Nếu Fc là lực ma sát thì: 
N
kA
N
4
' 1 
- Thời gian từ lúc bị ma sát đến khi dừng lại 
 ∆t = N’. T 
- Số lần qua VTCB của vật: khi 25,' nNn  (n nguyên) thì số lần qua 
VTCB sẽ là 2n; khi 
 75,'25, nNn  thì số lần qua VTCB của vật là 2n+1; khi 
 1'75,  nNn thì số lần qua VTCB của vật là 2n+2. 
 - Vị trí của vật có vận tốc cực đại: 
 Fc = Fhp => μ.m.g = K.x0 => 
0
mg
x
k

 
 - Vận tốc cực đại khi dao động đạt được tại vị trí x0 : 
Nguyễn Văn Dân – Long An - 0975733056 
 19 
0 0
v (A x ).   
VIII - DAO ĐỘNG CƯỠNG BỨC. CỘNG HƯỞNG 
- Khi vật dao động cưỡng bức thì tần số (chu kỳ) dao động của vật bằng 
tần số (chu kỳ) của ngoại lực. 
- Hiện tượng cộng hưởng xảy ra khi tần số (chu kỳ) của ngoại lực bằng tần 
số (chu kỳ) dao động riêng của hệ. 
Chú ý: Chu kỳ kích thích 
v
l
T  ; l là khoảng cách ngắn nhất giữa 2 mối 
ray tàu hỏa hoặc 2 ổ gà trên đường ; Vận tốc của xe để con lắc đặt trên 
xe có cộng hưởng: 
0
0
lf
T
l
v  
IX – CON LẮCTRÙNG PHÙNG 
 - Để xác định chu kỳ của 1 con lắc lò xo (hoặc con lắc đơn) người ta so 
sánh với chu kỳ T0 (đã biết) của 1 con lắc khác  0TT  . 
 - Hai con lắc này gọi là trùng phùng khi chúng đồng thời đi qua 1 vị trí 
xác định theo cùng một chiều 
 - Thời gian giữa hai lần trùng phùng: 
0
0
TT
TT

 
 Chú ý: + Nếu 0TT    nTTn  01 
 + Nếu 0TT    01 nTTn  (với 
*
Nn ) 
CHƯƠNG II: SÓNG CƠ HỌC 
I - ĐẠI CƯƠNG VỀ SÓNG CƠ HỌC 
 T: chu kỳ sóng; v: vận tốc truyền sóng;  : bước sóng 
Nguyễn Văn Dân – Long An - 0975733056 
 20 
1. Các công thức cơ bản 
 - Liên hệ giữa  , v và T (f): v f
T

  
 - Quãng đường sóng truyền đi được trong thời gian t: t
T
vtS

 
 - Vận tốc truyền sóng biết quãng đường sóng truyền được trong thời gian t 
là S: 
t
S
v  
 - Khoảng cách giữa n gợn lồi liên tiếp là d thì: 
1

n
d
 
 - n ngọn sóng đi qua trước mặt trong thời gian t thì: 
1

n
t
T 
 - Phao nhô cao n lần trong thời gian t thì: 
1

n
t
T 
2. Phương trình sóng 
 - Sóng truyền từ N qua O và đến M, giả sử biểu thức Sóng tại O có dạng: 
 )cos(0   tAu , thì: 
 )
2
cos(



x
tAuM  
 )
'2
cos(



x
tAuN  
 - Độ lệch pha của 2 điểm trên phương truyền s