Các bài toán chương 2 Hình học lớp 7 (Kèm đáp án)

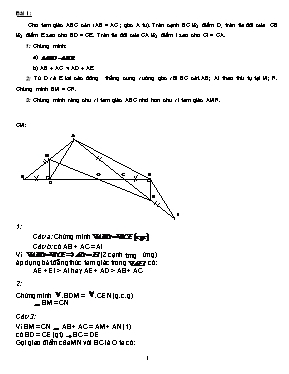
Bài I:
 Cho tam giác ABC cân (AB = AC ; góc A tù). Trên cạnh BC lấy điểm D, trên tia đối của CB lấy điểm E sao cho BD = CE. Trên tia đối của CA lấy điểm I sao cho CI = CA.
 1: Chứng minh:
	a) 
	b) AB + AC < AD + AE
 2: Từ D và E kẻ các đường thẳng cùng vuông góc với BC cắt AB; AI theo thứ tự tại M; N. Chứng minh BM = CN.
 3: Chứng minh rằng chu vi tam giác ABC nhỏ hơn chu vi tam giác AMN.
CM:
1: 
	Câu a: Chứng minh 
	Câu b: có AB + AC = AI
Vì (2 cạnh tương ứng)
áp dụng bất đẳng thức tam giác trong có:
	AE + EI > AI hay AE + AD > AB + AC
2:
Chứng minh vBDM = vCEN (g.c.g)
	 BM = CN
Câu 3:
Vì BM = CN AB + AC = AM + AN (1)
có BD = CE (gt) BC = DE
Gọi giao điểm của MN với BC là O ta có:
Từ (1) và (2) chu vi nhỏ hơn chu vi 
 Bài II:
 Cho tam giác ABC (AB > AC ) , M là trung điểm của BC . Đường thẳng vuông góc với tia phân giác của góc A tại M cắt cạnh AB , AC lần lượt tại E và F . 
 Chứng minh :
EH = HF 
.
 .
BE = CF .
C/m được (g-c-g) Suy ra EH = HF (đpcm)
 Từ Suy ra 
Xét có là góc ngoài suy ra 
 có là góc ngoài suy ra 
 vậy 
 hay (đpcm).
 áp dụng định lí Pytago vào tam giác vuông AFH : 
 ta có HF2 + HA2 = AF2 hay (đpcm)
C/m Suy ra AE = AF và 
Từ C vẽ CD // AB ( D EF ) C/m được 
 và có (cặp góc đồng vị) 
do do đó cân CF = CD ( 2)
Từ (1) và (2) suy ra BE = CF 
Bài III:Cho đoạn thẳng AB cú O là trung điểm. Trờn hai nửa mặt phẳng đối nhau bờ AB kẻ hai tia Ax // By. Lấy hai điểm C,E và D,F lần lượt trờn Ax và By sao cho AC = BD; CE = DF. Chứng minh:
Ba điểm: C, O, D thẳng hàng; E, O, F thẳng hàng.
ED = CF .
 Bài IV:
	Tam giỏc ABC cõn tại C và ; BD là phõn giỏc gúc B. Từ A kẻ tia Ax tạo với AB một gúc . Tia Ax cắt BD tại M, cắt BC lại E. BK là phõn giỏc gúc CBD, BK cắt Ax tại N.
Tớnh số đo gúc ACM.
So sỏnh MN và CE.
Câu V :
	Cho tam giác nhọn ABC; có đường cao AH. Trên nữa mặt phẳng bờ AC chứa điểm B vẽ tia AEAC và AE = AC. Trên nữa mặt phẳng bờ Ab chứa điểm C vẽ tia AFAB và AF = AB.
	a) C/M : EB = FC	
	b) Gọi giao điểm của EF với AH là N. C/M : N là trung điểm của EF.
Câu VI:
	Cho có Â = 600; BM, CN (M thuộc Ac và N thuộc AB) lần lượt là tia phân giác của và ; BM và CN cắt nhau tại I.
	a) Tính 	b) Chứng minh : 
Câu VII:
	Cho và có AB = A/B/, AC = A/C/. M thuộc BC sao cho MC = MB, M/ thuộc B/C/ sao cho M/C/ = M/B/ và AM = A/M/. Chứng minh : = .
Bài VIII
	Cho tam giỏc ABC cõn tại A (). Kẻ phõn giỏc BD (). Trờn tia AB lấy điểm M sao cho AM = BC.
Chứng minh BD + AD = BC
Tớnh 
Bài 4
(4 điểm)
Từ D kẻ DE//BC, trờn BC lấy điểm F sao cho BD = BF (1)
Chứng minh được DE = BE (tam giỏc BED cõn)
0.5 đ
Do tam giỏc AED cõn nờn AD =AE suy ra BE = CD
Vậy DE = CD
Tam giỏc BDF cõn cú nờn suy ra 
Vậy tam giỏc DFC cú 
Chứng minh được (2)
Từ (1) và (2) suy ra đpcm.
Dựng tam giỏc đều AMN sao cho N và C ở cựng một phớa so với AB. 
Vỡ 
 Suy ra AC = CN = AB 
vậy MC là trung trực của AN
Nờn 
 Cõu IX: Cho tam giỏc ABC. Ở phớa ngoài tam giỏc đú vẽ cỏc tam giỏc vuụng cõn tại A là ABD và ACE. 
Chứng minh CD = BE và CD vuụng gúc với BE.
 Kẻ đường thẳng đi qua A và vuụng gúc với BC tại H.
Chứng minh : Đường thẳng AH đi qua trung điểm của DE.
Lấy điểm K nằm trong tam giỏc ABD sao cho gúc ABK bằng 300, BA = BK.
Chứng minh: AK = KD.
4(7,0)
Vẽ hỡnh đỳng
a(3,0)
 vỡ cú: AD =AB(gt); ;
 AC = AE (gt) 
Suy ra DC = BE ( 2 cạnh tương ứng); ( 2 gúc tương ứng)
Gọi I là giao điểm của DC và AB.
Ta cú: ( đ đ); ( c/m trờn)
Mà suy ra 
Suy ra DC vuụng gúc với BE.
b(2,0)
Kẻ DM và EN lần lượt vuụng gúc với đường thẳng AH tại M và N.
Gọi F là giao điểm của DE và đường thẳng AH.
Ta c/m được (cạnh huyền – gúc nhọn)
Suy ra AH = DM
 ( cạnh huyền – gúc nhọn) suy ra AH = EN
Từ đú ta c/m được ( g.c.g)
Suy ra DF = DE
Hay đường thẳng AH đi qua trung điểm của DE.
c(1,5)
Vẽ tam giỏc đều BPD sao cho P và A nằm cựng phớa đối với BD
Ta cú: suy ra 
Suy ra suy ra (1)
Tam giỏc BAK cõn tại B cú gúc B = 300 nờn suy ra (2)
Từ (1) và (2) suy ra tam giỏc KDA cõn tại K suy ra KA = KD.
Bài X: Cho tam giỏc ABC vuụng cõn tại A, M là trung điểm BC. Lấy điểm D bất kỡ thuộc cạnh BC. H và I thứ tự là hỡnh chiếu của B và C xuống đường thẳng AD. Đường thẳng AM cắt CI tại N. Chứng minh rằng:
 a) BH = AI. 
 b) BH2 + CI2 cú giỏ trị khụng đổi.
 c) Đường thẳng DN vuụng gúc với AC.
 d) IM là phõn giỏc của gúc HIC. 
 C/M
N
Bài 6: (3 điểm): 
DAIC = DBHA ị BH = AI (0,75đ)
BH2 + CI2 = BH2 + AH2 = AB2 (0,75đ)
DBHM = DAIM ị HM = MI và éBMH = éIMA (0,5đ)
 mà : é IMA + éBMI = 900 ị éBMH + éBMI = 900 
 ị DHMI vuụng cõn ị éHIM = 450 
 mà : éHIC = 900 ịéHIM =éMIC= 450 ị IM là 
 phõn giỏc éHIC 
Cõu XI:ho tam giác ABC có AB < AC. Gọi M là trung điờ̉m của BC, từ M kẻ đường thẳng vuụng góc với tia phõn giác của góc BAC tại N và cắt tia AB tại E và cắt tia AC tại F. Chứng minh rằng: 
1)AE = AF 2) BE = CF
Cõu 4
(5 điờ̉m)
1
(1,5đ)
- Xét ANE và ANF có :
 AN chung
 (gt)
Suy ra : ANE =ANF (g – c - g)
 AE = AF (2 cạnh tương ứng)
2
(2đ)
- Từ C kẻ tia Cx // AB, cắt tia EF tại K 
- Xét BME và CMK có :
 MB = MC (gt)
 (đụ́i đỉnh) 
 (so le trong)
 Suy ra: BME = CMK (g – c - g)
 BE = CK (2 cạnh tương ứng) (1)
- Vì AE = AF nờn tam giác AEF cõn tại A, suy ra: 
 Mà: (đụ́i đỉnh) và (so le trong)
Suy ra: 
 tam giác CFK cõn tại C 
 CF = CK (2) 
Từ (1) và (2) suy ra: BE = CF (đpcm) 
3
(1,5đ)
Ta có: AE = AB + BE
 AF = AC – FC
 Suy ra: AE + AF = AB + BE + AC – FC = AB + AC
Mà: AE = AF, suy ra: 2.AE = AB + AC
 (đpcm)
Cõu XII:
 Cho tam giác ABC vuụng cõn tại A. Trờn cùng mụ̣t nửa mặt phẳng chứa điờ̉m A, bờ là BC vẽ các tia Bx và Cy cùng vuụng góc với BC. Lṍy M thuụ̣c cạnh BC ( M khác A và B); đường thẳng vuụng góc với AM tại A cắt Bx, Cy lõ̀n lượt tại H và K.
 a, Chứng minh: BM = CK
 b, Chứng minh A là trung điờ̉m của HK 
 c, Gọi P là giao điờ̉m của AB và MN, Q là giao điờ̉m của AC và MK. 
 Chứng minh: PQ song song với BC.
Cõu XIII: 
	Cho gúc xOy bằng vẽ phõ giỏc Az của gúc đú. Từ một điểm B thuộc tia Ax vẽ đường thẳng song song với Ay cắt Az tại C. Vẽ BH; CM vuụng gúc với Ay (H; M thuộc Ay) BK vuụng gúc với AC (K thuộc AC). Chứng minh rằng:
	a) K là trung điểm của AC
	b) BH = 
	c) Tam giỏc KMC đều