Bí kíp Casio để giải toán lượng giác - Cao Thành Thái

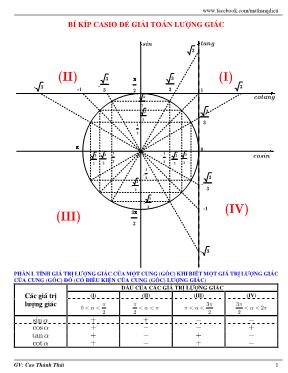
www.facebook.com/mathsnqdieu 
GV: Cao Thành Thái 1 
BÍ KÍP CASIO ĐỂ GIẢI TOÁN LƯỢNG GIÁC 
PHẦN I. TÍNH GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT CUNG (GÓC) KHI BIẾT MỘT GIÁ TRỊ LƯỢNG GIÁC 
CỦA CUNG (GÓC) ĐÓ (CÓ ĐIỀU KIỆN CỦA CUNG (GÓC) LƯỢNG GIÁC) 
Các giá trị 
lượng giác 
DẤU CỦA CÁC GIÁ TRỊ LƯỢNG GIÁC 
(I) (II) (III) (IV) 
0
2
π
α< < 
2
π
α π< < 
3
2
π
π α< < 
3
2
2
π
α π< < 
sinα + + − − 
cosα
+ − − + 
tanα + − + − 
cotα + − + − 
cosin
sin
cotang
tang
(IV)
(III)
(II) (I)
-
3
2
-
2
2
-
1
2
1
2
2
2
3
2
-
3
2
-
2
2
-
1
2
3
2
2
2
1
2
-
3
3
3
3
-
3
3
3
3
- 3
- 3 -1
-1
3
1
3
3pi
2
pi
pi
2
0
O
www.facebook.com/mathsnqdieu 
GV: Cao Thành Thái 2 
1. Đối với cung (góc) lượng giác thuộc gốc phần tư thứ nhất 
Lưu ý: các đơn đơn vi đo cung (góc) nên đổi về đơn vị độ. ( 180π → ° ). Máy tính hiển thị chế độ đo là độ 
Thuật toán: Tìm số đo cung (góc) thuộc đúng góc phần tư đã cho trước. 
Dạng 1. Cho sin x a= và 0
2
x
π
< < (hoặc 0 90x° < < ° ). Tính các giá trị lượng giác còn lại hoặc tính giá trị của 
biểu thức. 
Cách thức tính: 
- Bước 1: Bấm qj nhập giá trị của a rồi bấm ). 
- Bước 2: Tiếp tục bấm qJz để lưu giá trị vừa tính vào biến A. 
Dạng 2. Cho cosx a= và 0
2
x
π
< < (hoặc 0 90x° < < ° ). Tính các giá trị lượng giác còn lại hoặc tính giá trị của 
biểu thức. 
Cách thức tính: 
- Bước 1: Bấm qk nhập giá trị của a rồi bấm ). 
- Bước 2: Tiếp tục bấm qJz để lưu giá trị vừa tính vào biến A. 
Dạng 3. Cho tanx a= và 0
2
x
π
< < (hoặc 0 90x° < < ° ). Tính các giá trị lượng giác còn lại hoặc tính giá trị của 
biểu thức. 
Cách thức tính: 
- Bước 1: Bấm ql nhập giá trị của a rồi bấm ). 
- Bước 2: Tiếp tục bấm qJz để lưu giá trị vừa tính vào biến A. 
Dạng 4. Cho cotx a= và 0
2
x
π
< < (hoặc 0 90x° < < ° ). Tính các giá trị lượng giác còn lại hoặc tính giá trị của 
biểu thức. 
Cách thức tính: 
- Bước 1: Bấm ql1P nhập giá trị của a rồi bấm ). 
- Bước 2: Tiếp tục bấm qJz để lưu giá trị vừa tính vào biến A. 
Ví dụ: Cho 3sin
5
x = và 0
2
x
π
< < . Tính các giá trị lượng giác còn lại. 
Ta thực hiện bấm máy như sau: 
- Bước 1: Ta bấm qja3$5$)=. 
Ta được màn hình 1. 
- Bước 2: Ta không thoát màn hình mà tiếp tục bấm 
qJz. Ta được màn hình 2. 
- Bước 3: 
 + Tính cosx : bấm kQz)=. Ta được kết quả 4cos
5
x = . 
 + Tính tanx : bấm lQz)=. Ta được kết quả 3tan
4
x = . 
 + Tính cotx : bấm 1PlQz)=. Ta được kết quả 4cot
3
x = . 
www.facebook.com/mathsnqdieu 
GV: Cao Thành Thái 3 
Ví dụ: Cho cot 3a = và 0 90a° < < ° . Tính các giá trị lượng giác còn lại. 
- Bước 1: Ta bấm ql1P3)=. Ta được màn hình 1. 
- Bước 2: Ta không thoát màn hình mà tiếp tục bấm qJz. Ta 
được màn hình 2. 
- Bước 3: 
 + Tính sina : bấm jQz)=. Ta được kết quả sin 0,316a ≈ . 
 + Tính cosa : bấm kQz)=. Ta được kết quả cos 0,949a ≈ 
 + Tính tana : bấm lQz)=. Ta được kết quả 1tan
3
a = . 
Để hiển thị kết quả dạng căn thức đối với các kết quả của sina và cosa ta thực hiện 
như sau: 
 + jQz)= tiếp tục bấm d= rồi bấm sM=. Ta được 10sin
10
a = . 
 + kQz)= tiếp tục bấm d= rồi bấm sM=. Ta được 3 10cos
10
a = . 
2. Đối với cung (góc) lượng giác thuộc gốc phần tư thứ hai 
Dạng 1. Cho sin x a= và 
2
x
π
π< < (hoặc 90 180x° < < ° ). Tính các giá trị lượng giác còn lại hoặc tính giá trị 
của biểu thức. 
Cách thức tính: 
- Bước 1: Bấm qj nhập giá trị của a rồi bấm ). 
- Bước 2: Tiếp tục bấm 180pM=. 
- Bước 3: Tiếp tục bấm qJz để lưu giá trị vừa tính vào biến A. 
Dạng 2. Cho cosx a= và 
2
x
π
π< < (hoặc 90 180x° < < ° ). Tính các giá trị lượng giác còn lại hoặc tính giá trị 
của biểu thức. 
Cách thức tính: 
- Bước 1: Bấm qk nhập giá trị của a rồi bấm ). 
- Bước 2: Tiếp tục bấm qJz để lưu giá trị vừa tính vào biến A. 
Dạng 3. Cho tanx a= và 
2
x
π
π< < (hoặc 90 180x° < < ° ). Tính các giá trị lượng giác còn lại hoặc tính giá trị 
của biểu thức. 
Cách thức tính: 
- Bước 1: Bấm ql nhập giá trị của a rồi bấm ). 
- Bước 2: Tiếp tục bấm 180+M=. 
- Bước 3: Tiếp tục bấm qJz để lưu giá trị vừa tính vào biến A. 
Dạng 4. Cho cotx a= và 
2
x
π
π< < (hoặc 90 180x° < < ° ). Tính các giá trị lượng giác còn lại hoặc tính giá trị 
của biểu thức. 
Cách thức tính: 
- Bước 1: Bấm ql1P nhập giá trị của a rồi bấm ). 
- Bước 2: Tiếp tục bấm 180+M=. 
- Bước 3: Tiếp tục bấm qJz để lưu giá trị vừa tính vào biến A. 
www.facebook.com/mathsnqdieu 
GV: Cao Thành Thái 4 
Ví dụ: Cho 3sin
5
x = và 90 180x° < < ° . Tính các giá trị lượng giác còn lại. 
- Bước 1: Ta bấm qja3$5$)=. Ta được kết 
quả như hình 1. Vì kết quả 36,86989765 không thuộc góc phần tư (II) 
nên ta áp dụng kiến thức ở trên, ta thực hiện tiếp 
- Bước 2: Không thoát màn hình ta tiếp tục bấm 
180pM=. Ta được màn hình 2. Ta thấy kết quả này thỏa. 
- Bước 3: Tiếp tục bấm qJz. Ta được màn hình 3. 
- Bước 4: 
 + Tính cosx : bấm kQz)=. Ta được kết quả 4cos
5
x =− . 
 + Tính tanx : bấm lQz)=. Ta được kết quả 3tan
4
x =− . 
 + Tính cotx : bấm 1PlQz)=. Ta được kết quả 4cot
3
x =− . 
3. Đối với cung (góc) lượng giác thuộc gốc phần tư thứ ba 
Dạng 1. Cho sin x a= và 3
2
x
π
π < < (hoặc 180 270x° < < ° ). Tính các giá trị lượng giác còn lại hoặc tính giá trị 
của biểu thức. 
Cách thức tính: 
- Bước 1: Bấm qj nhập giá trị của a rồi bấm ). 
- Bước 2: Tiếp tục bấm z180pM=. 
- Bước 3: Tiếp tục bấm qJz để lưu giá trị vừa tính vào biến A. 
Dạng 2. Cho cosx a= và 3
2
x
π
π < < (hoặc 180 270x° < < ° ). Tính các giá trị lượng giác còn lại hoặc tính giá trị 
của biểu thức. 
Cách thức tính: 
- Bước 1: Bấm qk nhập giá trị của a rồi bấm ). 
- Bước 2: Tiếp tục bấm zM=. 
- Bước 3: Tiếp tục bấm qJz để lưu giá trị vừa tính vào biến A. 
Dạng 3. Cho tanx a= và 3
2
x
π
π < < (hoặc 180 270x° < < ° ). Tính các giá trị lượng giác còn lại hoặc tính giá 
trị của biểu thức. 
Cách thức tính: 
- Bước 1: Bấm ql nhập giá trị của a rồi bấm ). 
- Bước 2: Tiếp tục bấm 180+M=. 
- Bước 3: Tiếp tục bấm qJz để lưu giá trị vừa tính vào biến A. 
Dạng 4. Cho cotx a= và 3
2
x
π
π < < (hoặc 180 270x° < < ° ). Tính các giá trị lượng giác còn lại hoặc tính giá trị 
của biểu thức. 
Cách thức tính: 
- Bước 1: Bấm ql1P nhập giá trị của a rồi bấm ). 
- Bước 2: Tiếp tục bấm 180+M=. 
- Bước 3: Tiếp tục bấm qJz để lưu giá trị vừa tính vào biến A. 
www.facebook.com/mathsnqdieu 
GV: Cao Thành Thái 5 
Ví dụ: Cho 3cos
2
α = − và 
2
π
π α− < <− . Tính giá trị của biểu thức tan
1 sin
P
α
α
=
+
. 
Trước tiên, ta xét 
2
π
π α− < <− biểu diễn trên đường tròn lượng giác. Ta thấy α nằm trên góc phần tư thứ ba. 
Do đó ta bấm máy như sau: 
- Bước 1: Ta bấm qkazs3$$2$)=. Ta được màn hình 1. 
- Bước 2: Tiếp tục bấm zM=. Ta được màn hình 2. 
- Bước 3: Tiếp tục bấm qJz. Ta được màn hình 3. 
- Bước 4: Để tính giá trị của biểu thức P ta nhập như sau: 
alQz)$1+jQz)=. Ta được kết 
quả 2 3
3
P = . 
4. Đối với cung (góc) lượng giác thuộc gốc phần tư thứ tư 
Dạng 1. Cho sin x a= và 3 2
2
x
π
π< < (hoặc 180 270x° < < ° ). Tính các giá trị lượng giác còn lại hoặc tính giá 
trị của biểu thức. 
Cách thức tính: 
- Bước 1: Bấm qj nhập giá trị của a rồi bấm ). 
- Bước 2: Tiếp tục bấm qJz để lưu giá trị vừa tính vào biến A. 
Dạng 2. Cho cosx a= và 3 2
2
x
π
π< < (hoặc 180 270x° < < ° ). Tính các giá trị lượng giác còn lại hoặc tính giá 
trị của biểu thức. 
Cách thức tính: 
- Bước 1: Bấm qk nhập giá trị của a rồi bấm ). 
- Bước 2: Tiếp tục bấm zM=. 
- Bước 3: Tiếp tục bấm qJz để lưu giá trị vừa tính vào biến A. 
Dạng 3. Cho tanx a= và 3 2
2
x
π
π< < (hoặc 180 270x° < < ° ). Tính các giá trị lượng giác còn lại hoặc tính giá 
trị của biểu thức. 
Cách thức tính: 
- Bước 1: Bấm ql nhập giá trị của a rồi bấm ). 
- Bước 2: Tiếp tục bấm qJz để lưu giá trị vừa tính vào biến A. 
Dạng 4. Cho cotx a= và 3 2
2
x
π
π< < (hoặc 180 270x° < < ° ). Tính các giá trị lượng giác còn lại hoặc tính giá 
trị của biểu thức. 
Cách thức tính: 
- Bước 1: Bấm ql1P nhập giá trị của a rồi bấm ). 
- Bước 2: Tiếp tục bấm qJz để lưu giá trị vừa tính vào biến A. 
Ví dụ: Cho tan 2α = − và 0
2
π
α− < < . Tính giá trị của biểu thức 
2
2 cos
1 sin
P
α
α
+
=
+
. 
Trước tiên, ta xét 0
2
π
α− < < biểu diễn trên đường tròn lượng giác. Ta thấy α nằm trên góc phần tư thứ tư. 
Do đó ta bấm máy như sau: 
www.facebook.com/mathsnqdieu 
GV: Cao Thành Thái 6 
- Bước 1: Ta bấm qlz2)=. Ta được màn hình 1. 
- Bước 2: Tiếp tục bấm qJz. Ta được mành hình 2. 
- Bước 3: Để tính giá trị của biểu thức P ta nhập như sau: 
a2+kQz)$1+jQz)d=. Ta được kết quả 
1, 360P ≈ . 
PHẦN II. TÍNH GIÁ TRỊ CỦA BIỂU THỨC LƯỢNG GIÁC KHI BIẾT CUNG 
(GÓC) LƯỢNG GIÁC THỎA MÃN ĐẲNG THỨC CHO TRƯỚC 
1. Cho tanx a= hoặc cotx a= , tính giá trị của biểu thức. 
Cách thức tính: 
- Bước 1: Bấm ql giá trị của a )= hoặc bấm ql1Pgiá trị của a )=. 
- Bước 2: Tiếp tục bấm qJz để lưu giá trị vừa tính vào biến A. Sau đó tính giá trị của biểu thức. 
Ví dụ: Cho tan 3α = . Tính giá trị của biểu thức 
3 3
3 sin 2cos
5 sin 4 cos
M
α α
α α
−
=
+
. 
- Bước 1: Ta bấm ql3)=. Ta được màn hình 1. 
- Bước 2: Không thoát màn hình ta tiếp tục bấm qJz. Ta được màn hình 2. 
Để tính giá trị của biểu thức ta nhấn như sau: 
a3jQz)p2kQz)$5jQz)^3$+4kQz
)^3= 
Ta được kết quả 70
139
M = . 
2. Cho cung (góc) lượng giác thỏa ( )f mα = , tính giá trị của biểu thức 
Cách thức tính: 
- Bước 1: Trước tiên ta tìm giá trị của cung α bằng lệnh SOLVE. Ta thực hiện như sau: nhập biểu thức ( )f mα = , 
sau đó bấm qr. Nhập giá trị bất kỳ khi màn hình xuất hiện “X?”, sau đó bấm =. Kiểm tra điều kiện của 
cung (góc) lượng giác (nếu có). 
- Bước 2: Tiếp tục bấm qJz để lưu giá trị vừa tính vào biến A. Sau đó tính giá trị của biểu thức. 
Ví dụ: Tính giá trị của biểu thức 2sin 3 sin 2A α α= + , biết 2cos2 7 sin 0α α+ = . 
- Bước 1: Ta nhập biểu thức để tìm α như sau: 
2k2Q))+7jQ))Qr0 
Ta được màn hình 1. 
Tiếp tục bấm qr. Ta được màn hình 2. 
Nhập giá trị bất kỳ cho X 1=. Ta được màn hình 3. 
- Bước 2: Tiếp tục ta bấm qJz ta được màn hình 4. 
Để tính giá trị của biểu thức ta nhập như sau: 
j3Qz)+j2Qz)d= 
Ta được kết quả 29
64
A =− . 
3. Cho cung (góc) lượng giác thỏa sin cosa b cα α+ = , tính giá trị của biểu thức 
Cách thức tính: 
- Bước 1: Trước tiên biểu diễn sin cosa b cα α+ = về dạng ( )2 2 sina b cα θ+ + = với 
2 2
cos
a
a b
θ =
+
, 
2 2
sin
b
a b
θ =
+
. Khi đó biểu thức ( )2 2 sina b cα θ+ + = tương đương 
www.facebook.com/mathsnqdieu 
GV: Cao Thành Thái 7 
 ( )
2 2
sin
c
a b
α θ⇔ + =
+
1
2 2
1
2 2
sin
180 sin
c
a b
c
a b
α θ
α θ
−
−
  
   = −     +
⇔       = °− −     +
1 1
2 2 2 2
1 1
2 2 2 2
sin cos
180 sin cos
c a
a b a b
c a
a b a b
α
α
− −
− −
    
       = −              + +
⇔             = °− −             + +
- Bước 2: Nhập dòng thứ nhất của công thức trong khung trên và lưu vào biến biến A. Nhập dòng thứ hai của công 
thức trong khung trên và lưu vào biến biến B. 
Sau đó nhập biểu thức để tính giá trị. 
Ví dụ: Cho góc nhọn α thỏa mãn 6 cos 8 sin 5 3α α+ = . Tính gần đúng giá trị của biểu thức: 
4 3 24 cos 4 3cos 2 cos cos 1S α α α α= + + + + . 
- Bước 1: Biến đổi 6 cos 8 sin 5 3α α+ = . 
 8 sin 6 cos 5 3α α⇔ + = . 
2 2 2 2 2 2
8 6 5 3
sin cos
8 6 8 6 8 6
α α⇔ + =
+ + +
. 
4 3 3
sin cos
5 5 2
α α⇔ + = . 
 ( ) 3sin
2
α θ⇔ + = với 4cos
5
θ = ; 
3
sin
5
θ = . 
- Bước 2: Tìm các giá trị của α thỏa yêu cầu góc nhọn. Ta lần lượt nhập như sau: 
qjas3$$2$)pqka4$5$)= 
ta được giá trị thỏa mãn như màn hình 1. 
Tiếp tục ta bấm qJz, ta được màn hình 2. 
Tiếp tục tìm giá trị thứ hai của α . Ta bấm như sau: 
180pqjas3$$2$)pqka4$5$)=. Ta được giá 
trị thỏa mãn như màn hình 3. 
Tiếp tục ta bấm qJx, ta được màn hình 4. 
Ta lần lượt tính giá trị của biểu thức với hai giá trị của α vừa tìm. 
 + Ứng với giá trị của biến A 
4k4Qz)^4$+3kQz)^3$+2kQz)d+k
Qz)+1= 
Ta được kết quả 5,94415S ≈ . 
 + Ứng với giá trị của biến B 
4k4Qx)^4$+3kQx)^3$+2kQx)d+k 
Qx)+1= 
www.facebook.com/mathsnqdieu 
GV: Cao Thành Thái 8 
Ta được kết quả 3,63134S ≈ . 
PHẦN III. CHỨNG MINH ĐẲNG THỨC LƯỢNG GIÁC KHÔNG PHỤ THUỘC VÀO ẨN SỐ 
Cơ sở lý thuyết: Một biểu thức lượng giác ( )f x được gọi là không phụ thuộc vào x (hay đọc lập với x ) nếu ( )f x c= 
với mọi x (trong đó c là hằng số). 
Cách thức tính: 
- Bước 1: Nhập biểu thức ( )f x vào máy tính (nên dùng biến nhớ X). 
- Bước 2: Sử dụng r tìm giá trị của ( )f x . 
Ví dụ: Chứng minh biểu thức sau không phụ thuộc x : sin cos
4 4
A x x
π π      = + − −            
. 
- Bước 1: Đổi (rad) 45
4
π
= ° . Nhập biểu thức như sau: 
j45+Q))pk45pQ)) 
Ta được màn hình 1. 
- Bước 2: Bấm r. Ta được màn hình 2. 
Nhập giá trị của X vào (lần lượt lấy hai giá trị bất kỳ). Chẳng hạn: 
15X = . Ta được kết quả 0A = . 
Tiếp tục bấm r 75X = . Ta được kết quả 0A = . 
Vậy 0A = với mọi x . 
PHẦN IV. RÚT GỌN ĐẲNG THỨC LƯỢNG GIÁC 
Để rút gọn biểu thức lượng giác ( )f x thành biểu thức lượng giác ( )g x (hay chứng minh đẳng thức lượng giác 
( ) ( )f x g x= ) ta thực hiện xét hiệu ( ) ( )f x g x− và thế ít nhất hai giá trị của x vào biểu thức ( ) ( )f x g x− xem 
( ) ( )f x g x− có bằng 0 hay không. Nếu với tất cả các giá trị x ta có ( ) ( ) 0f x g x− = thì ta nói ( )f x được rút gọn 
thành ( )g x (hay đẳng thức ( ) ( )f x g x= được chứng minh). 
Ví dụ: Rút gọn của biểu thức 4 2 2sin sin cosP x x x= + là 
A. 2cos x . B. 2sin x . C. cos2x . D. sin 2x . 
Ta lần lượt thử các đáp án: 
- Đối với đáp án A. 
Xét hiệu 4 2 2 2sin sin cos cosx x x x+ − . Ta thực hiện bấm máy biểu thức vừa có: 
jQ))^4$+jQ))dOkQ))dpkQ))d ta 
được màn hình 1. 
Bấm r xuất hiện màn hình 2. 
Ta thử với 15X = . Ta được kết quả 
0, 866 0− ≠ . Vậy đáp án A không thỏa. 
- Đối với đáp án B. 
Xét hiệu 4 2 2 2sin sin cos sinx x x x+ − . Ta thực hiện bấm máy biểu thức vừa có: 
jQ))^4$+jQ))dOkQ))dpjQ))d ta 
được màn hình 1. 
Bấm r xuất hiện màn hình 2 
Ta thử với 15X = . Ta được kết quả 0 . 
Tiếp tục với 75X = . Ta được kết quả 0 . 
Vậy đáp án B thỏa.