Bảng công thức lượng giác
Bạn đang xem tài liệu "Bảng công thức lượng giác", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
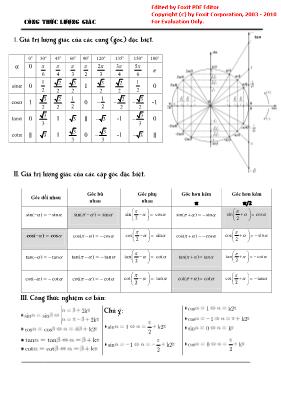
CÔNG THỨC LƯỢNG GIÁC I. Giá trị lượng giác của các cung (góc) đặc biệt. II. Giá trị lượng giác của các cặp góc đặc biệt. III. Công thức nghiệm cơ bản: 2k sin sin 2k cos cos k2 tan tan k cot cot k Chú ý: sin 1 k2 2 sin 1 k2 2 cos 1 k2 cos 1 k2 sin 0 k cos 0 k 2 α 0 o 30 o 45 o 60 o 90 o 120 o 135 o 150 o 180 o 0 6 4 3 2 2 3 3 4 5 6 sinα 0 1 2 2 2 3 2 1 3 2 2 2 1 2 0 cosα 1 3 2 2 2 1 2 0 1 2 2 2 3 2 -1 tanα 0 3 3 1 3 ∥ 3 -1 3 3 0 cotα ∥ 3 1 3 3 0 3 3 -1 3 ∥ Gĩc đối nhau Gĩc bù nhau Gĩc phụ nhau Gĩc hơn kém 𝛑 Gĩc hơn kém 𝛑/2 sin( ) sin sin( ) sin sin cos 2 sin( ) sin sin cos2 cos( ) cos cos( ) cos cos sin 2 cos( ) cos cos sin2 tan( ) tan tan( ) tan tan cot 2 tan( ) tan tan cot2 cot( ) cot cot( ) cot cot tan 2 cot( ) cot cot tan2 tan CÔNG THỨC LƯỢNG GIÁC IV. Công thức lượng giác . 1. Công thức cơ bản: 2 2 sin cos 1 tan .cot 1 2 2 1 1 tan cos 2 2 1 1 cot sin 2. Công thức cộng: sin( ) sin .cos sin .cosa b a b b a cos(a b) cosa.cosb sina.sin b tan a tan b tan(a b) 1 tan a.tan b 3. Công thức nhân đôi: sin2 2sin .cos 2 2 2 2 cos2 cos sin 2 cos 1 1 2sin 2 2 2 tan tan 2 1 tan cot 1 cot 2 2 cot Hệ quả: (Công thức hạ bậc hai) 2 2 2 1 cos2 sin 2 1 cos2 cos 2 1 cos2 tan 1 cos2 4. Công thức nhân ba: 3 sin3 3sin 4sin 3 3 2 cos3 4 cos 3cos 3tan tan tan3 1 3tan Hệ quả: (Công thức hạ bậc ba) 3 1sin 3 sin sin 3 4 3 1cos 3cos cos 3 4 5. Công thức biến đổi tổng thành tích: cos cos 2cos .cos 2 2 a b a b a b cos cos 2sin .sin 2 2 a b a b a b sin sin 2sin .cos 2 2 a b a b a b sin sin 2cos .sin 2 2 a b a b a b 6. Công thức biến đổi tích thành tổng: 7. Công thức bổ xung: cos sin 2 cos 4 2 sin 4 sin cos 2 sin 4 2 cos 4 2 1 sin2 cos sin 2 tan cot sin2 cot tan 2cot2 sin4α + cos4 α = 1 - 2 1 sin 2 2 α = 1 3 cos4 4 4 sin6 α + cos6α = 1 - 4 3 sin 2 2 α = 3 5 cos4 8 8 8. Công thức biểu diễn theo t = tan 2 . 2 2t sin 1 t 2 2 1 t cos 1 t 2 2t tan 1 t 1 cos .cos cos( ) cos( ) 2 1 sin .sin cos( ) cos( ) 2 1 sin .cos sin( ) sin( ) 2 a b a b a b a b a b a b a b a b a b
Tài liệu đính kèm:
 bang-cong-thuc-luong-giac-dung-cho-10-11-12.pdf
bang-cong-thuc-luong-giac-dung-cho-10-11-12.pdf





