Bài toán Tứ giác lớp 8

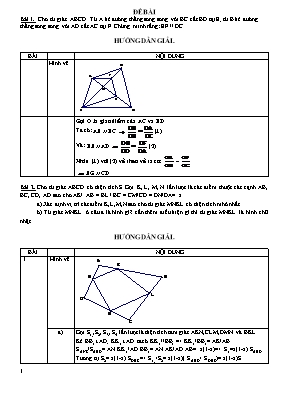
ĐỀ BÀI
Bài 1. Cho tứ giác ABCD. Từ A kẻ đường thẳng song song với BC cắt BD tại E; từ B kẻ đường thẳng song song với AD cắt AC tại F. Chứng minh rằng: EF // DC.
HƯỚNG DẪN GIẢI.
BÀI
NỘI DUNG
Hình vẽ
Gọi O là giao điểm của AC và BD
Ta cĩ: AE // BC (1)
Và: BF // AD (2)
Nhân (1) với (2) vế theo vế ta có: 
 EG // CD
Bài 2. Cho tứ giác ABCD cĩ diện tích S. Gọi K, L, M, N lần lượt là các điểm thuộc các cạnh AB, BC, CD, AD sao cho AK/ AB = BL / BC = CM/CD = DN/DA= x.
a) Xác định vị trí các điểm K,L,M,N sao cho tứ giác MNKL cĩ diện tích mhỏ nhất.
b) Tứ giác MNKL ở câu a là hình gì? cần thêm điều kiện gì thì tứ giác MNKL là hình chữ nhật.
HƯỚNG DẪN GIẢI.
BÀI
NỘI DUNG
1
Hình vẽ
a)
Gọi S1,,S2, S3, S4 lần lượt là diện tích tam giác AKN,CLM,DMN và BKL.
Kẻ BB1^AD; KK1^AD ta cĩ KK1//BB1 => KK1/BB1= AK/AB
SANK/SABD= AN.KK1/AD.BB1= AN.AK/AD.AB= x(1-x)=> S1=x(1-x) SABD
Tương tự S2= x(1-x) SDBC=> S1,+S2= x(1-x)( SABD+ SDBC)= x(1-x)S 
Tương tự S3+S4= x(1-x)S
S1,+S2+ S3+ S4= x(1-x)2S 
SMNKL=S-( S1,+S2+ S3+ S4)= 2S x2-2Sx+S=2S(x-1/2)2+1/2S³1/2S
Vậy SMNKL đạt giá trị nhỏ nhất bằng 1/2S khi x=1/2 khi đĩ M,N,K,L lần lượt là trung điểm các cạnh CD, DA, AB, BC
b)
Tứ giác MNKL ở câu a là hình bình hành 
Tứ giác MNKL ở câu a là hình chữ nhật khi BD^AC
Bài 3. Cho tứ giác ABCD có AD = BC. Gọi M, N lần lượt là trung điểm của AB, CD. Tia MN cắt tia AD ở E và cắt tia BC ở F. Chứng ninh rằng: .
HƯỚNG DẪN GIẢI.
BÀI
NỘI DUNG
1
Hình vẽ
Gọi I là trung điểm của BD, ta có: 
 BF // IN => 
 AE // MI => 
Xét MNI có:
IM = IN (2 đường trung bình)
=> MNI cân tại I
=> 
=>