Bài tập về Sóng cơ Vật lí lớp 12 (Có đáp án) - Phần 1

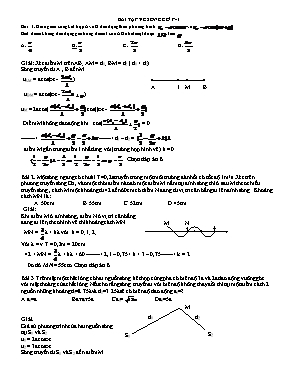
BÀI TẬP VỀ SÓNG CƠ P-1
Bài 1. Hai nguồn song kết hợp A và B dao động theo phương trình và
Biết điểm không dao động gần trung điểm I của AB nhất một đoạn .Tìm 
A.	B.	C. 	 D. 
 · ·
 I M
·
B
·
A
Giải: Xét điểm M trên AB; AM = d1; BM = d2 ( d1 > d2)
Sóng truyền từ A , B đến M
 uAM = acos(wt - ) 
 uBM = acos(wt - )
uM = 2acos(cos((wt - .
 Điểm M không dao động khi cos( = 0
-------> ------> d1 – d2 = 
 điểm M gần trung điểm I nhất ứng với (trường hợp hình vẽ) k = 0
 . Chọn đáp án B
Bài 2. Một sóng ngang có chu kì T=0,2s truyền trong một môi trường đàn hồi có tốc độ 1m/s. Xét trên phương truyền sóng Ox, vào một thời điểm nào đó một điểm M nằm tại đỉnh sóng thì ở sau M theo chiều truyền sóng , cách M một khoảng từ 42 đến 60cm có diểm N đang từ vị tri cân bằng đi lên đỉnh sóng . Khoảng cách MN là: 
 A. 50cm B.55cm C.52cm D.45cm
 Giải:
M
N
Khi điểm M ở đỉnh sóng, điểm N ở vị trí cân bằng
đang đi lên, theo hình vẽ thì khoảng cách MN
 MN = l + kl với k = 0; 1; 2; ...
Với l = v.T = 0,2m = 20cm
 42 2,1 – 0,75 k = 2
 Do đó MN = 55cm. Chọn đáp án B
Bài 3.Trên mặt một chât lỏng có hai nguồn sóng kêt hợp cùng pha có biên độ 3a và 2a dao động vuông góc với mặt thoáng của chất lỏng.Nếu cho rằng sóng truyền đi với biên độ không thay đổi thì tại một điểm cách 2 nguồn những khoảng d1=8.75λvà d2=3.25λ sẽ có biên độ dao động a0=?
d2
d1
M
S1
S2
A a0=a	Ba≤a0≤5a	Ca0=	Da0=5a
Giải.
Giả sử phương trình của hai nguốn sóng
tại S1 và S2
u1 = 2acoswt.
u2 = 3acoswt.
Sóng truyền từ S1 và S2 đến điểm M
u1M = 2acos(wt -) = 2acos(wt -17,5π) 
u2M = 3acos(wt -) = 3acos(wt - 6,5π) 
Ta thấy u1M và u2M ngược pha nhau. 
Do đó biên độ dao động tại M là a0 = 3a -2a = a. Chọn đáp án A
Bài 4.. Nguồn sóng ở O dao động với tần số 10Hz.Dao động truyền đi với vận tốc 0.4m/s trên dây dài, trên phương này có hai điểm P và Q theo thứ tự đó PQ=15cm. Cho biên độ a=10mm và biên đọ không thay đổi khi sóng truyền . Nếu tại thời điểm nào đó P có li độ 0.5cm di chuyển theo chiều dương thì li độ tại Q là
 A -1cm	B. 8.66cm	C. -0.5cm	D. -8.66cm
 Giải: Bước sóng l = v/f = 0,4/10 = 0,04 m = 4 cm
Q
·
P
·
O
·
Giả sử biểu thức của sóng tại nguồn O
u0 = 10cos20πt (mm) OP = d (cm)
Biểu thức của sóng tại P uP = 10cos(20πt -) = 10cos(20πt -0,5πd) 
Biểu thức của sóng tại Q uQ = 10cos(20πt -) = 10cos(20πt - 0,5πd -7,5π) 
Ta có: uQ = 10cos(20πt - 0,5πd -7,5π) 
= 10cos(20πt - 0,5πd )cos7,5π + 10sin(20πt - 0,5πd )sin 7,5π = -10 sin(20πt - 0,5πd )
Theo bài ra uP = 10cos(20πt -0,5πd) = 5 mm----> cos(20πt -0,5πd) = 0,5 
------> sin(20πt -0,5πd) = ± 
vP = u’P = - 200πsin(20πt -0,5πd) >0 ------>sin (20πt -0,5πd) <0
uQ = -10 sin(20πt - 0,5πd ) = 8,66 mm Do đó uQ = 8,66 mm. Chọn đáp án B
Bài 5 : Tại hai điểm A và B trên mặt nước cách nhau 8 cm có hai nguồn kết hợp dao động với phương trình: , tốc độ truyền sóng trên mặt nước là . Xét đoạn thẳng CD = 4cm trên mặt nước có chung đường trung trực với AB. Khoảng cách lớn nhất từ CD đến AB sao cho trên đoạn CD chỉ có 3 điểm dao dộng với biên độ cực đại là: 
A. 3,3 cm. 	B. 6 cm.	 C. 8,9 cm.	 D. 9,7 cm. 
Giải:
 Bước sóng λ = v/f = 30/20 = 1,5 cm
h
d2
d1
M
C
A
B
D
Khoảng cách lớn nhất từ CD đến AB mà trên CD chỉ có 3 điểm 
dao đông với biên độ cực đai khi tại C và D thuộc các vân cực đai
bậc 1 ( k = ± 1)
 Tại C: d2 – d1 = 1,5 (cm)
 Khi đó AM = 2cm; BM = 6 cm
Ta có d12 = h2 + 22
 d22 = h2 + 62
Do đó d22 – d12 1,5(d1 + d2 ) = 32
 d2 + d1 = 32/1,5 (cm)
 d2 – d1 = 1,5 (cm)
 Suy ra d1 = 9,9166 cm
 . Chọn nđáp án D