Bài tập Toán 12 - Học kỳ I - Trường THCS – THPT Phan Châu Trinh

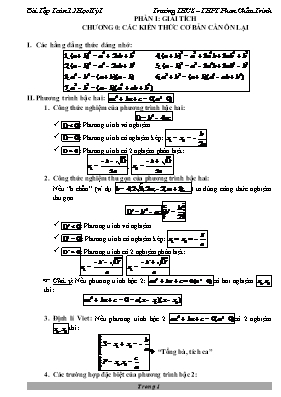
PHẦN I: GIẢI TÍCH
CHƯƠNG 0: CÁC KIẾN THỨC CƠ BẢN CẦN ÔN LẠI
Các hằng đẳng thức đáng nhớ:
Phương trình bậc hai: 
Công thức nghiệm của phương trình bậc hai: 
: Phương trình vô nghiệm.
: Phương trình có nghiệm kép: 
: Phương trình có 2 nghiệm phân biệt:
; 
Công thức nghiệm thu gọn của phương trình bậc hai: 
Nếu “b chẵn” (ví dụ ) ta dùng công thức nghiệm thu gọn.
: Phương trình vô nghiệm.
: Phương trình có nghiệm kép: 
: Phương trình có 2 nghiệm phân biệt:
; 
F Chú ý: Nếu phương trình bậc 2: có hai nghiệm thì:
Định lí Viet: Nếu phương trình bậc 2 có 2 nghiệm thì:
— “Tổng bà, tích ca”
Các trường hợp đặc biệt của phương trình bậc 2: 
Nếu thì phương trình có nghiệm: 
Nếu thì phương trình có nghiệm: 
Dấu của nghiệm số: 
Phương trình có 2 nghiệm dương phân biệt 
Phương trình có 2 nghiệm dương 
Phương trình có 2 nghiệm âm phân biệt 
Phương trình có 2 nghiệm âm 
Phương trình có 2 nghiệm cùng dấu 
Phương trình có 2 nghiệm trái dấu 
Dấu của đa thức:
Dấu của nhị thức bậc nhất: 
trái dấu a	0	cùng dấu a
“Phải cùng, trái trái”
Dấu của tam thức bậc hai: 
	cùng dấu a
cùng dấu a	0	cùng dấu a	
cùng dấu a	0	trái dấu a	0	cùng dấu a
“Trong trái, ngoài cùng”
Dấu của đa thức bậc 3: Bắt đầu từ ô bên phải cùng dấu với hệ số a của số mũ cao nhất, qua nghiệm đơn đổi dấu, qua nghiệm kép không đổi dấu.
Điều kiện để tam thức không đổi dấu trên .
Cho tam thức bậc hai: 
Phương trình lượng giác cơ bản
Đặc biệt: 
Đặc biệt: 
Phương trình và bất phương trình chứa trị tuyệt đối
Phương trình : 
Bất phương trình:
Phương trình và bất phương trình vô tỉ
Phương trình:
Bất phương trình:
Công thức tính đạo hàm
“anh bạn ăn cơm bằng chén”
CHƯƠNG I: ỨNG DỤNG ĐẠO HÀM ĐỀ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
§1. SỰ ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ
KIẾN THỨC CƠ BẢN:
1. Định nghĩa: Giả sử hàm số xác định trên khoảng K.
Hàm số f được gọi là đồng biến (tăng) trên khoảng K nếu:
Hàm số f được gọi là nghịch biến (giảm) trên khoảng K nếu:
 	Hàm số đồng biến hoặc nghịch biến trên khoảng K được gọi chung là hàm số đơn điệu trên khoảng K.
Nếu hàm số đồng biến trên K thì đồ thị đi lên từ trái sang phải
Nếu hàm hàm số nghịch biến trên K thì đồ thị đi xuống từ trái sang phải
2. Định lý: Giả sử hàm số có đạo hàm trên khoảng K.
	a) Nếu thì hàm số f đồng biến trên khoảng K.
	b) Nếu thì hàm số f nghịch biến trên khoảng K.
	c) Nếu thì hàm số f không đổi (f là hàm hằng) trên khoảng K.
Lưu ý: Ở ý a) và b) của định lý trên có thể bằng 0 tại một số hữu hạn điểm thì kết luận vẫn đúng.
BÀI TẬP:
Vấn đề 1: Xét sự đồng biến, nghịch biến của hàm số
Phương pháp: Để xét sự đồng biến, nghịch biến của hàm số, ta thực hiện các bước như sau:
Tìm tập xác định.
Tính đạo hàm . Giải phương trình .
Lập bảng biến thiên. 
Từ bảng biến thiên kết luận các khoảng đồng biến, nghịch biến của hàm số.
Xét sự đồng biến, nghịch biến của các hàm số sau:
a) 	b) 	
c) 	d) 
e) 	f) 
g) 	h) 	
i) 	k) 	
l) 	m)
n) 	o) 	
p) 	q) 	
r) 	s) 
Tìm các khoảng đơn điệu của các hàm số:
a) 	b) 	
c) 	d) 	
e) 	f) 
g) 	h) 	
i) 	j) 	
k) 	l) 
m) 	n) 
o) 	p) 
r) 	s) 
u) 	v)
Vấn đề 2: Tìm điều kiện của tham số m để hàm số đơn điệu trên tập xác định
Phương pháp:
Hàm bậc 3: 
Tập xác định .
Đạo hàm là 1 tam thức bậc 2. 
Hàm số đồng biến trên 
Hàm số nghịch biến trên 
Hàm nhất biến: 
Tập xác định 
Đạo hàm có dấu phụ thuộc vào dấu của tử.
Hàm số đồng biến trên từng khoảng xác định
 (Không có dấu “=”)
Hàm số nghịch biến trên từng khoảng xác định
 (Không có dấu “=”)
Tìm điều kiện của tham số để hàm số sau đồng biến trên tập xác định:
Tìm m để hàm số:
 nghịch biến trên .
 đồng biến trên .
 đồng biến trên .
Tìm các giá trị của tham số m để hàm số 
Nghịch biến trên từng khoảng xác định.
Đồng biến trên từng khoảng xác định.
Định m để hàm số:
 đồng biến trên từng khoảng xác định.
 nghịch biến trên từng khoảng xác định.
Tìm m để các hàm số sau luôn đồng biến trên :
Tìm m để các hàm số sau luôn nghịch biến trên :
(*)Tìm m để hàm số nghịch biến trên khoảng .
(*)Tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên khoảng .
(*)Tìm các giá trị của tham số để hàm số nghịch biến trên khoảng (ĐH Khối A-2013)
(*)Tìm tất cả các giá trị của tham số m để hàm số đồng biến trên khoảng .
(*)Tìm m để hàm số đồng biến trên khoảng .
§2. CỰC TRỊ CỦA HÀM SỐ
KIẾN THỨC CƠ BẢN:
1. Định nghĩa: Cho hàm số xác định và liên tục trên tập D (D ) và .
Nếu tồn tại khoảng và sao cho , thì ta nói hàm số đạt cực đại tại .
Nếu tồn tại khoảng và sao cho , thì ta nói hàm số đạt cực tiểu tại .
a	b
	f(x0)
a	b
	f(x0)
Chú ý:
Nếu hàm số đạt cực đại (cực tiểu) tại thì được gọi là điểm cực đại (điểm cực tiểu) của hàm số; được gọi là giá trị cực đại (giá trị cực tiểu) của hàm số và được ký hiệu là fCĐ(fCT) hay yCĐ(yCT), còn điểm được gọi là điểm cực đại (điểm cực tiểu) của đồ thị hàm số.
Các điểm cực đại và điểm cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại (giá trị cực tiểu) còn gọi là cực đại (cực tiểu) và được gọi chung là cực trị của hàm số.
2. Định lý:
Định lý 1: Giả sử hàm số liên tục trên khoảng chứa điểm và có đạo hàm trên khoảng .
Nếu đổi dấu từ dương sang âm khi qua thì hàm số đạt cực đại tại .
Nếu đổi dấu từ âm sang dương khi qua thì hàm số đạt cực tiểu tại .
	+	
	fCĐ
	+
	fCT
Định lý 2: Giả sử hàm số có đạo hàm cấp hai trong khoảng . Khi đó:
Nếu thì hàm số đạt cực tiểu tại .
Nếu thì hàm số đạt cực đại tại .
BÀI TẬP:
Vấn đề 1: Tìm cực trị của hàm số
Phương pháp: 
Qui tắc 1: Dùng định lý 1.
Tìm tập xác định.
Tính đạo hàm . Giải phương trình .
Lập bảng biến thiên. 
Từ bảng biến thiên suy ra các điểm cực trị.
Qui tắc 2: Dùng định lý 2.
Tìm tập xác định.
Tính đạo hàm . Giải phương trình tìm các nghiệm 
Tính và 
Dựa vào dấu của suy ra các điểm cực trị:
Nếu thì hàm số đạt cực tiểu tại .
Nếu thì hàm số đạt cực đại tại .
Chú ý: Quy tắc 2 thường dùng đối với hàm số lượng giác hoặc việc xét dấu phức tạp.
Tìm cực trị của các hàm số sau:
a)	b)
c)	d)
e)	f)
Tìm các khoảng đơn điệu và cực trị của các hàm số sau:
a)	b)
c)	d)
Dựa vào quy tắc 2 tìm cực trị (nếu có) của các hàm số:
a)	b)
c)	d)
e)	d)
Vấn đề 2: Tìm điều kiện để hàm số có cực trị
Phương pháp: 
Hàm số đạt cực trị tại 
Hàm số đạt cực đại tại 
Hàm số đạt cực tiểu tại 
Hàm bậc 3: 
Hàm số có 2 cực trị (cực đại và cực tiểu) phương trình có 2 nghiệm phân biệt
Hàm số không có cực trị Phương trình vô nghiệm hoặc có nghiệm kép
Hàm bậc 4 trùng phương: 
Ta có:
Hàm số có 3 cực trị Phương trình có 3 nghiệm phân biệt Phương trình (2) có 2 nghiệm phân biệt khác 0.
Hàm số có 1 cực trị Phương trình có 1 nghiệm Phương trình (2) vô nghiệm hoặc có nghiệm kép bằng 0.
Tìm m để hàm số có 2 cực trị.
Tìm m để hàm số có cực đại và cực tiểu.
Tìm m để hàm số đạt cực tiểu tại .
Tìm m để hàm số đạt cực đại tại .
Cho hàm số . Tìm m để hàm số:
a)Đạt cực đại tại .
b)Đạt cực tiểu tại .
c)Có hai cực trị.
Định m để các hàm số sau có 2 cực trị:
Định m để hàm số:
 đạt cực đại tại 
 đạt cực tiểu tại .
 đạt cực trị tại . Khi đó hàm số đạt cực đại hay cực tiểu?
Tìm m để hàm số đạt cực tiểu tại .
Định để hàm số 
Không có cực trị.
Có cực đại và cực tiểu.
Có đồ thị nhận làm một điểm cực trị.
(*) Tìm giá trị của tham số để đồ thị của hàm số 
Có 2 điểm cực trị nằm về 2 phía của trục tung.
Có cực đại và cực tiểu.
Có 2 điểm cực trị có hoành độ âm.
(*)Tìm m để hàm sốđạt cực trị tại x1 , x2 thỏa mãn 
(*)Cho hàm số . Định m để hàm số có hai điểm cực trị có hoành độ dương.
(*)Cho hàm số . Tìm m để hàm số đạt cực trị tại thoả mãn 
(*)Cho hàm số .Tìm m để hàm số có cực đại cực tiểu đồng thời .
Cho hàm số .
Tìm a, b để hàm số đạt cực trị bằng khi .
Với a, b vừa tìm được hãy xác định các khoảng đơn điệu và cực trị của hàm số.
Xác định m để đồ thị của hàm số có cực tiểu mà không có cực đại.
Tìm m để hàm số có 3 cực trị.
Tìm m để hàm số có 1 cực trị.
Cho hàm số . Xác định m để hàm số chỉ có 1 cực trị.
Cho hàm số . Tìm a để hàm số có 3 cực trị.
Cho hàm số . Xác định các giá trị của tham số k để hàm số có 1 cực trị.
Cho hàm số . Định a, b để hàm số đạt cực trị bằng tại .
Xác định giá trị tham số để hàm số đạt cực trị tại . Khi đó hàm số đạt cực đại hay cực tiểu tại .
Tìm để hàm số:
 có cực đại, cực tiểu.
 có cực đại, cực tiểu.
 đạt cực đại tại .
Vấn đề 3: Đường thẳng đi qua hai điểm cực trị của hàm bậc ba
Phương pháp: Cho hàm số bậc ba .
Chia cho ta được
Khi đó, giả sử , là các điểm cực trị thì:
Suy ra phương trình của đường thẳng qua hai điểm cực đại và cực tiểu là 
Viết phương trình đường thẳng qua hai điểm cực trị của đồ thị các hàm số:
a)
b)
c)
(*)Tìm các giá trị của tham số để hàm số có cực đại, cực tiểu. Lập phương trình đường thẳng đi qua 2 điểm cực trị:
a)(ĐHQG –2001)
b)(ĐHTS – 1999)
c) 
§3. GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ
KIẾN THỨC CƠ BẢN:
Cho hàm số xác định trên tập D.
Số M được gọi là giá trị lớn nhất của hàm số trên tập D nếu với mọi thuộc D và tồn tại sao cho 
Ký hiệu 
Số m được gọi là giá trị nhỏ nhất của hàm số trên tập D nếu với mọi thuộc D và tồn tại sao cho 
Ký hiệu 
BÀI TẬP:
Vấn đề 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên 1 đoạn
Phương pháp: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên 1 đoạn :
Tìm tập xác định Hàm số liên tục trên đoạn 
Tính đạo hàm .
Tìm các điểm làm bằng 0 hoặc không xác định. 
Tính , , 
So sánh và kết luận.
Tìm giá trị lớn nhất,giá trị nhỏ nhất của các hàm số :
 trên 	
 trên đoạn 
 trên đoạn 
 trên đoạn 
 trên đoạn 
 trên đoạn 
 trên đoạn 
 trên đoạn 	
 trên đoạn 
 trên đoạn 
 trên đọan 
 trên đoạn 
Tìm giá trị lớn nhất,giá trị nhỏ nhất của các hàm số :
Tìm giá trị lớn nhất,giá trị nhỏ nhất của các hàm số :
 trên đoạn 
 trên đoạn 
Vấn đề 2: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên 1 khoảng hoặc nửa khoảng
Phương pháp: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên 1 khoảng hoặc nửa khoảng 
Tìm tập xác định.
Tính đạo hàm 
Lập bảng biến thiên
Dựa vào bảng biến thiên, so sánh và kết luận.
Tìm giá trị lớn nhất, giá trị nhỏ nhất (nếu có) của các hàm số sau:
a)	b) 
c)	d) trên khoảng 
Tìm các giá trị của tham số m để giá trị nhỏ nhất của hàm số trên đoạn bằng . (TN – 2012)
§4: ĐƯỜNG TIỆM CẬN
A-KIẾN THỨC CƠ BẢN:
Đường thẳng được gọi là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số nếu ít nhất một trong các điều kiện sau được thoả mãn:
;	 
;	
Đường thẳng được gọi là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số nếu ít nhất một trong các điều kiện sau được thoả mãn:
;	
Chú ý: Đối với hàm số phân thức hữu tỷ 
Nếu có nghiệm thì đồ thị có tiệm cận đứng .
Nếu bậc()£ bậc() thì đồ thị có tiệm cận ngang.
B- BÀI TẬP:
Tìm tất cả các tiệm cận của đồ thị của hàm số sau: 	
a) 	b)	c) 	d)	
e)	f)	g)	h)
Tìm tất cả các tiệm cận của đồ thị hàm số sau:
a)	b)	c)	d)
e)	f)	g)	
(*) Cho hàm số có đồ thị (C).
Chứng minh rằng tích các khoảng cách từ một điểm đến các đường tiệm cận của (C) là một hằng số.
Tìm các điểm trên (C) sao cho điểm đó cách đều các đường tiệm cận của (C).
§5. KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
KIẾN THỨC CƠ BẢN:
Các bước chung khảo sát sự biến thiên và vẽ đồ thị hàm số:(6 dấu *)
Tập xác định:
Giới hạn (và tiệm cận đối với hàm phân thức )
Đạo hàm: 
Đối với hàm bậc 3, bậc 4: Giải phương trình tìm nghiệm.
Đối với hàm phân thức :(hoặc ) 
Bảng biến thiên:
Nhận xét về chiều biến thiên và cực trị.
Bảng giá trị:(5 điểm đối với hàm bậc 3, bậc 4; 6 điểm đối với hàm phân thức )
Chú ý: Đối với hàm bậc ba, nếu phương trình vô nghiệm thì khi lập bảng giá trị ta giải phương trình để tìm điểm là điểm chính giữa của bảng giá trị. (điểm được gọi là điểm uốn của đồ thị)
Vẽ đồ thị:
BÀI TẬP:
Vấn đề 1: Khảo sát sự biến thiên và vẽ đồ thị hàm số bậc ba
Các dạng đồ thị của hàm số bậc ba 
Số nghiệm của phương trình 
 có 2 nghiệm phân biệt
 có nghiệm kép
 vô nghiệm
Khảo sát sự biến thiên và vẽ đồ thị các hàm số bậc ba sau: 
a)	b) 
c) 	d) 
e)	f)
g)	h)
i)	j)
k) 	l) 
m) 	n) 
Vấn đề 2: Khảo sát sự biến thiên và vẽ đồ thị hàm số bậc bốn trùng phương
Các dạng đồ thị của hàm số bậc bốn trùng phương 
 có 3 nghiệm phân biệt
 có 1 nghiệm duy nhất
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số bậc bốn sau:
a)	b) 
c)	d)
e)	f)
g)	h)
i) 	j) 
Vấn đề 3: Khảo sát sự biến thiên và vẽ đồ thị hàm số phân thức
Các dạng đồ thị của hàm số phân thức 
Khảo sát sự biến thiên và vẽ đồ thị các hàm số phân thức:
a)	b)
c)	d)
e)	f)
g)	h)
§6. MỘT SỐ BÀI TOÁN LIÊN QUAN ĐẾN KHẢO SÁT HÀM SỐ
SỰ TƯƠNG GIAO CỦA HAI ĐỒ THỊ
Vấn đề 1 : Tìm giao điểm của hai đường.
Phương pháp : 
Cho hai đồ thị và . 
Phương trình hoành độ giao điểm của và là : (*)
Giải phương trình (*) ta được hoành độ giao điểm, thế vào 1 trong 2 hàm số hoặc được tung độ giao điểm.
Tìm giao điểm của hai đường :
 và 
 và 
 và 
 và 
 và 
Vấn đề 2: Tìm điều kiện của tham số m để hai đường cong cắt nhau với số điểm cho trước.
Phương pháp : 
Cho hai đồ thị và . 
Phương trình hoành độ giao điểm của và là : (*)
 và cắt nhau tại điểm phân biệt khi và chỉ khi phương trình (*) có nghiệm phân biệt.
Lưu ý : 
Trục hoành có phương trình .
Đường thẳng qua điểm và có hệ số góc m có phương trình là 
Tìm để đồ thị các hàm số:
 cắt nhau tại hai điểm phân biệt.
 cắt nhau tại hai điểm phân biệt.
 cắt nhau tại hai điểm phân biệt.
 cắt nhau tại hai điểm phân biệt.
 cắt nhau tại ba điểm phân biệt. 
 cắt nhau tại ba điểm phân biệt. 
 cắt nhau tại bốn điểm phân biệt.
Tìm để đồ thị hàm số:
 cắt trục hoành tại ba điểm phân biệt.
 cắt trục hoành tại ba điểm phân biệt.
 cắt trục hoành tại ba điểm phân biệt.
 cắt trục hoành tại bốn điểm phân biệt.
 cắt trục hoành tại bốn điểm phân biệt.
Chứng minh đồ thị các hàm số sau luôn cắt nhau tại 2 điểm phân biệt với mọi giá trị của 
Cho hàm số 
Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho.
Tìm tất cả các giá trị của tham số để đường thẳng cắt đồ thị của hàm số đã cho tại hai điểm phân biệt.
Tìm để:
Đường thẳng d qua có hệ số góc m cắt Parabol tại 2 điểm phân biệt.
Đường thẳng d qua có hệ số góc m cắt đồ thị tại 3 điểm phân biệt.
Vấn đề 3: Dùng đồ thị biện luận theo tham số m số nghiệm của phương trình.
Phương pháp:
Cho đồ thị . Dùng đồ thị (C), biện luận theo m số nghiệm của phương trình .
Biến đổi phương trình về dạng (*). 
Số nghiệm của phương trình (*) là số giao điểm của hai đồ thị : 
Bảng kết quả :
Số giao điểm
Số nghiệm
Lưu ý: Nếu bài toán chỉ yêu cầu tìm các giá trị của m để phương trình có đúng 3 nghiệm, 4 nghiệm, ta không cần lập bảng kết quả như trên mà chỉ cần chỉ rõ các trường hợp thỏa đề (Dựa vào đồ thị ta thấy (C) và (d) cắt nhau tại đúng 3 điểm, đúng 4 điểm )
Cho hàm số 
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. 
Dựa vào đồ thị (C), biện luận theo tham số số nghiệm của phương trình: 
Dựa vào đồ thị (C), biện luận theo tham số số nghiệm của phương trình: 
Dựa vào đồ thị (C), tìm m để phương trình có đúng 1 nghiệm.
Dựa vào đồ thị (C), tìm m để phương trình có đúng 2 nghiệm.
Dựa vào đồ thị (C), tìm m để phương trình có ít nhất 2 nghiệm.
Cho hàm số 
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. 
Dựa vào đồ thị (C), biện luận theo tham số số nghiệm của phương trình: 
Cho hàm số (1)
Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1). 
Dựa vào đồ thị (1), biện luận theo tham số số nghiệm của phương trình . 
Cho hàm số 
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. 
Biện luận theo tham số số nghiệm của phương trình: .
Cho hàm số 
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. 
Biện luận theo tham số số nghiệm của phương trình: .
Cho hàm số 
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. 
Tìm điều kiện của để phương trình có 4 nghiệm phân biệt.
Cho hàm số 
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. 
Tìm điều kiện của để phương trình có 1 nghiệm duy nhất.
VIẾT PHƯƠNG TRÌNH TIẾP TUYẾN CỦA ĐỒ THỊ HÀM SỐ
Phương pháp:
Cho hàm số có đồ thị là đường cong (C). Phương trình tiếp tuyến của đồ thị tại điểm là: 
Lưu ý: Ta phải tìm được 3 đại lượng: 
Dạng 1: Viết phương trình tiếp tuyến khi biết hoành độ tiếp điểm 
Tính đạo hàm 
Thay vào tính 
Thay vào tính 
Phương trình tiếp tuyến: 
Dạng 2: Viết phương tiếp tuyến khi biết tung độ tiếp điểm .
Giải phương trình tìm .
Thay vào tính 
Phương trình tiếp tuyến: 
Dạng 3: Viết phương trình tiếp tuyến khi biết hệ số góc .
Giả sử tiếp điểm là 
Giải phương trình tìm .
Thay vào ta tìm được .
Phương trình tiếp tuyến: 
Lưu ý: 
Nếu tiếp tuyến song song với đường thẳng thì .
Nếu tiếp tuyến vuông góc với đường thẳng thì .
Cho hàm số có đồ thị (C). Viết phương trình tiếp tuyến của (C):
Tại các giao điểm của (C) với trục hoành. 	
Tại điểm có hoành độ bằng 4.
Biết tiếp tuyến có hệ số góc . 
Biết tiếp tuyến song song với đường thẳng .
Biết tiếp tuyến vuông góc với đường thẳng 
Cho đường cong . Viết phương trình tiếp tuyến của (C): 
Tại điểm có hoành độ bằng .
Tại điểm có tung độ bằng 3.
Biết tiếp tuyến song song với đường thẳng .
Cho hàm số: :
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
Viết phương trình tiếp tuyến của (C) tại điểm có tung độ . 
Cho hàm số: :
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
Viết phương trình tiếp tuyến của đồ thị (C) tại giao điểm của (C) với trục tung.
Cho hàm số: 
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
Viết phương trình tiếp tuyến của đồ thị (C) tại điểm .
Viết phương trình tiếp tuyến của đồ thị (C) biết tiếp tuyến song song với đường thẳng .
Cho hàm số :
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
Viết phương trình tiếp tuyến của đồ thị (C) tại điểm .
Viết phương trình các đường thẳng vuông góc với đường thẳng và tiếp xúc với đồ thị (C) hàm số 
Cho hàm số :
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
Viết phương trình tiếp tuyến của đồ thị (C) tại điểm là nghiệm của phương trình .
Cho hàm số 
Viết phương trình tiếp tuyến của (C) tại điểm .
(*)Tiếp tuyến cắt , lần lượt tại A và B. Tính diện tích tam giác OAB.
MỘT SỐ BÀI TẬP TỔNG HỢP
Cho hàm số có đồ thị (C).
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
Gọi A là điểm thuộc đồ thị (C) có hoành độ bằng 4, viết phương trình tiếp tuyến với đồ thị (C) tại điểm A.
Cho hàm số .
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
Viết phương trình tiếp tuyến của (C) tại điểm có hoành độ bằng .
Viết phương trình tiếp tuyến với (C) biết tiếp tuyến song song với phân giác góc phần tư thứ nhất.
Tìm m để đường thẳng cắt (C) tại 2 điểm phân biệt.
Cho hàm số 
Tìm m để cắt trục hoành tại 4 điểm phân biệt.
Khảo sát và vẽ đồ thị (C) khi .
(*)Viết phương trình tiếp tuyến của (C) biết tiếp tuyến đi qua .
Cho hàm số 
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
Biện luận theo số nghiệm của phương trình .
Viết phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục tung.
Tìm giá trị lớn nhất của hàm số trên đoạn .
Cho hàm có đồ thị (C)
Khảo sát và vẽ đồ thị (C) 
Dùng đồ thị (C) biện luận theo số nghiệm phương trình 
Viết phương trình tiếp tuyến của (C) tại điểm cực đại.
Cho hàm số có đồ thị (C)
Khảo sát và vẽ đồ thị (C).
Dùng đồ thị (C) tìm m để phương trình có 4 nghiệm phân biệt.
Viết phương trình tiếp tuyến của (C) tại điểm có hoành độ bằng 2.
Cho hàm số có đồ thị (H)
Khảo sát và vẽ đồ thị (H).
Viết phương trình tiếp tuyến của (H) tại giao điểm của (H) với trục tung.
Cho hàm có đồ thị (C)
Khảo sát và vẽ đồ thị (C) .
Viết phương trình tiếp tuyến của đồ thị (C) tại điểm là nghiệm của phương trình .
Tìm các giá trị của tham số m để phương trình sau đây có nhiều hơn 2 nghiệm: 
Cho hàm có đồ thị (C)
Khảo sát và vẽ đồ thị (C) .
Viết phương trình tiếp tuyến của đồ thị (C) tại điểm thuộc (C) có hoành độ bằng 2.
Viết phương trình tiếp tuyến của đồ thị (C) biết tiếp tuyến có hệ số góc bằng 9.
Tìm điều kiện của m để phương trình có 3 nghiệm phân biệt.
Cho hàm số 
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
Biện luận theo số nghiệm của phương trình .
Viết phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục hoành.
Viết phương trì