Bài tập ôn tập Hình học 7 – Chương I

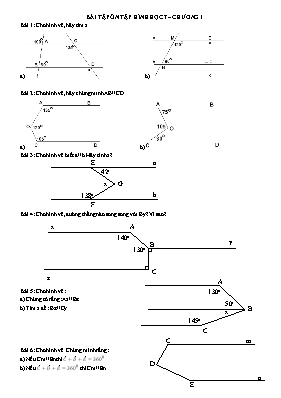
BÀI TẬP ÔN TẬP HÌNH HỌC 7 – CHƯƠNG I
Bài 1: Cho hình vẽ, hãy tìm x.
a) b)
Bài 2: Cho hình vẽ, hãy chứng minh AB//CD
a) b)
E
420
x
G
1380
F
a
b
Bài 3: Cho hình vẽ biết a//b. Hãy tính x?
Bài 4: Cho hình vẽ, đường thẳng nào song song với By? Vì sao?
x
z
A
B
y
C
1400
1300
B
A
C
500
x
1450
1300
Bài 5: Cho hình vẽ: 
a) Chứng tỏ rằng: Ax//Bz
b) Tìm x để: Bz//Cy
C
D
E
m
n
Bài 6: Cho hình vẽ. Chứng mình rằng:
a) Nếu Cm//En thì C+D+E=3600
b) Nếu C+D+E=3600 thì Cm//En
Bài 7: Chứng minh rằng hai tia phân giác của hai góc kề bù thì vuông góc với nhau.
Bài 8: Cho góc xOy và góc yOz là hai góc kề bù. Tia Om là phân giác của góc xOy. Trên cùng một nửa mặt phẳng bờ xz chứa tia Oy, vẽ tia On sao cho: On vuông góc với Om. Chứng minh rằng: Tia On là tia phân giác của góc yOz.
Bài 9: Cho đường thẳng xy, lấy điểm O thuộc xy. Trên nửa mặt phẳng bờ xy vẽ hai tia Oa, Ob sao cho xOa=yOb<900. Vẽ tia Om vuông góc với xy. Chứng minh rằng: tia Om là phân giác góc aOb.
Bài 10: Cho góc xOy nhọn. Từ điểm M trên cạnh Ox, dựng MN vuông góc với Oy tại N, dựng NP vuông góc với Ox tại P, dựng PQ vuông góc với Oy tai Q, dựng QR vuông góc với Ox tại R. Chứng minh rằng: 
a) MN//PQ; NP//QR	b) Tìm tất cả các góc bằng góc PNM
Bài 11: Cho góc bẹt AOB. Trên cùng một nửa mặt phẳng bờ AB, vẽ 2 tia OM và OM sao cho AOM=BON=300 
a) Hai góc AOM và BON có đối đỉnh không?
b) Vẽ tia OE sao cho tia OB là phân giác của góc NOE. Hai góc AOM và BOE có đối đỉnh không? Vì sao?
Bài 12: Cho tam giác ABC có B=500. Trên tia đối của tia AB lấy điểm O. Trên nửa mặt phẳng không chứa C bờ AB vẽ xOB=500.
a) Chứng minh rằng: Ox//BC.	b) Qua A vẽ d//BC, Chứng minh rằng: ABC+BAC+ACB=1800
Bài 13: Cho tam giác ABC có A=2B. Tia phân giác của góc A cắt BC ở D. Vẽ DE//AB, căt AC ở E. Vẽ EF//AD, cắt BC ở F. Vẽ FG//DE, cắt AC ở D.
a) Những góc đỉnh A, D, E, F nào bằng B 
b) DE, EF, FG là phân giác của những góc nào? Vì sao?
Bài 14: Cho MON=1200. Vẽ OP và OQ nằm giữa hai tia OM và ON sao cho OP vuông góc với OM; OQ vuông góc với ON
a) So sánh hai góc MOQ và NOP	b) Tính số đo góc POQ
Bài 15: Cho ∆ ABC, phân giác BM (M ∈ AC). Vẽ MN // AB cắt BC tại N. Phân giác góc MNC cắt MC ở P.
CMR: MBC = BMN, BM // NP
Gọi NQ là phân giác của BNM, cắt AB ở Q. CMR: NQ ⊥ BM
Bài 14: Cho xOy = 1200. Lấy A ∈ Ox, B ∈ Oy. Vẽ tia Am, An trong xOy sao cho xAm = 700, OBn = 1300. Chứng minh Am // Bn.
Bài 16: Cho xOy và A ∈ Ox, B ∈ Oy. Qua A dựng đường thẳng a ⊥ Ox. Qua B dựng đường thẳng b ⊥ Oy. Chứng minh rằng:
a) Nếu a cắt b thì xOy < 1800 	 b) Nếu a // b thì xOy = 1800 	c) Nếu a ⊥ b thì xOy = 900
Bài 17: Cho ∆ ABC. Trên cạnh AB lấy M, trên nửa mặt phẳng bờ AB chứa C, vẽ tia Mx sao cho AMx = B
CMR: Mx // BC và Mx cắt AC
Gọi D là giao điểm của Mx với AC. Lấy N nằm giữa C và D. Trên nửa mặt phẳng bờ AC không chứa điểm B, vẽ tia Ny sao cho CNy = C. CMR: Mx // Ny
Bài 18: Qua A ở ngoài đường thẳng a, vẽ 101 đường thẳng phân biệt.CMR:có ít nhất 100 đường thẳng cắt a.
Bài 19: Cho ∆ ABC, phân giác AD, qua B kẻ đường thẳng d // AD.
Chứng tỏ: d cắt AC tại E	b) CMR: ABE = AEB
Vẽ m qua A và vuông góc với AD, cắt BE tại F. CMR: AF là phân giác của EAB và m⊥EB
Bài 20: Cho ∆ABC. Vẽ phân giác ngoài tại A của ∆ABC. Từ B kẻ d//AD.
CMR: d cắt AC tại E	b) CMR: ABE = AEB
Từ B kẻ b ⊥ AD, từ A kẻ a // b. CMR: b ⊥ d và a là phân giác góc BAC.
Bài 21: Vẽ hình và viết giả thiết, kết luận của định lí sau : 
 Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ 3 thì chúng song song với nhau.
 	Bài 22: a) Hãy viết định lí nói về một đường thẳng vuông góc với một trong hai đường thẳng song song.
 b) Vẽ hình minh họa, viết GT/KL bằng kí hiệu
Bài 23: Phát biểu định lí, viết GT, KL được diễn tả bởi hình vẽ sau:
 a A 
 b B
Bài 24: 
a) Hãy phát biểu định lí được diễn tả bởi hình vẽ sau.
b) Viết giả thiết và kết luận của định lí đó bằng kí hiệu
Bài 25: Vẽ hình, viết giả thiết, kết luận của định lí: “Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau.”
Bài 26 : Vẽ hình, viết giả thiết, kết luận và chứng minh định lí: “Nếu hai đường thẳng cùng vuông goc với một đường thẳng thứ ba thì chúng song song với nhau.”
Bài 27: 
Cho hình 1: ( a //b, B2=40)
a) Chỉ ra góc so le trong, đồng vị, trong cùng phía với góc B2.
b) Tính số đo các góc: B4
c) Tính số đo các góc: A2; A4.
a
b
A
B
1
2
3
4
4
1
2
3
400
Hình 1
Bài 28: 
Cho hình vẽ (hình 2). 
1) Vì sao m // n?
2) Tính số đo x của góc ABD
x
n
m
1200
B
A
D
C
Hình 2
Bài 29: Vẽ hình theo trình tự sau:
 a) Góc xOy có số đo 600 , điểm A nằm trong góc xOy
 b) Đường thẳng m đi qua A và vuông góc với Ox
 c) Đường thẳng n đi qua A và song song với Oy 
Bài 30: Cho đoạn thẳng AB dài 12cm. Hãy vẽ đường trung trực của đoạn thẳng ấy. Nêu rõ cách vẽ.
Bài 31: Hình vẽ sau cho biết a//b
 A=40; AOB=90,. 
Tính số đo của góc B1 
Bài 32: Cho hình vẽ. Biết :
xAO=30; AOB=100; OBy=110
Chứng minh: xx’ // yy’.
Bài 33: Cho hình vẽ, biết Ax// By, xAB= 1200, BCz= 1200. 
Tính số đo ABy? 
Các cặp đường thẳng nào song song với nhau ? vì sao? 
 B y
 z C
x A 
Bài 34: Cho hình vẽ. Biết B1 = 400; C2 = 400
a) Đường thẳng a có song song với đườngthẳng b không ? Vì sao?
b) Đường thẳng b có song song với đườngthẳng c không ? Vì sao?
H.2
1300
c) Đường thẳng a có song song với đườngthẳng c không ? Vì sao?
Bài 35: Cho hình vẽ (H.2), có B1 =1300 thì: Số đo của góc A1 là: 
700
a
b
Bài 36: 
Cho hình vẽ: Biết a // b. A= 700, A= 900. 
Tính số đo của góc B1 và D1
450
300
Bài 37: 
Cho hình vẽ sau: Biết A= 300 ; B= 450; 
AOB = 750.
 	Chứng minh rằng : a // b
Bài 38: Cho hình vẽ bên. Biết E là trung điểm của AB ; ME vuông góc AB tại E và ME, MF lần lượt là tia phân giác của AMB và AMC.
1/ Vì sao EM là đường trung trực của đoạn thẳng AB ?
2/ Chứng tỏ rằng: MF//AB