Bài ôn tập môn Toán 12 năm 2017

dfsdfdsfsdfdsfdsfsdfsdfdsfsdfsdfdsfdsfsdfsdfdsfsdfdsfdsfsdfsdfsdfsdfs
Câu 1: Cho số phức Tìm môđun của số phức 
	A. 	B. 	C. 	D. 
Câu 2: Tìm tập nghiệm S của phương trình 
	A. S = {1}	B. 	C. S ={2}	D. S = {5}
Câu 3: Cho hàm số . Mệnh đề nào dưới đây đúng?
	A. Hàm số không có điểm cực trị.
	B. Hàm số có đúng một điểm cực trị.
	C. Hàm số có đúng hai điểm cực trị
	D. Hàm số có đúng ba điểm cực trị
Câu 4: Cho mặt phẳng Điểm nào trong các phương án dưới đây thuộc mặt phẳng (P)
	A. 	B. 	C. 	D. 
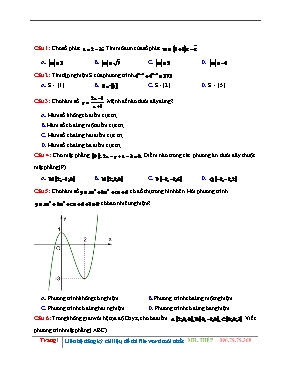
Câu 5: Cho hàm số có đồ thị trong hình bên. Hỏi phương trình
 có bao nhiêu nghiệm? 
	A. Phương trình không có nghiệm	B. Phương trình có đúng một nghiệm. 
	C. Phương trình có đúng hai nghiệm. 	D. Phương trình có đúng ba nghiệm
Câu 6: Trong không gian với hệ tọa độ Oxyz, cho ba điểm . Viết phương trình mặt phẳng ( ABC).
	A. 	B. 
	C. 	D. 
Câu 7: Cho hàm số Mệnh đề nào dưới đây đúng? 
	A. Hàm số đồng biến trên 
	B. Hàm số đồng biến trên và nghịch biến trên 
	C. Hàm số nghịch biến trên 
 	D. Hàm số nghịch biến trên , Hàm số đồng biến trên 
Câu 8: Với các số phức z thỏa mãn, tập hợp các điểm biểu diễn của số phức z là một đường tròn. Tìm bán kính R của đường tròn đó. 
	A. 	B. 	C. R = 8	D. R = 4.
Câu 9: Mệnh đề nào dưới đây là sai?
	A. , với mọi hàm f(x), g(x) liên tục trên R.
	B. , với mọi hàm f(x), g(x) liên tục trên R.
	C. với mọi hằng số k và với mọi hàm f(x) liên tục trên R.
	D. với mọi hàm f(x) có đạo hàm trên R
Câu 11: Tính tích phân 
	A. 	B. 	C. 	D. 
Câu 12: Tìm giá trị lớn nhất của hàm số trên đoạn 
	A. 	B. 	C. 	D. 
Câu 13: Tập xác định của hàm số là
	A. 	B. 
	C. 	D. 
Câu 14: Cho số phức thỏa mãn Tính tổng 
A. 	B. 	C. 	D. 
Câu 15: Cho Một hình nón có bán kính đáy bằng a và góc ở đỉnh bằng 600. Diện tích xung quanh của hình nón đó là 
	A. 	B. 	C. 	D. 
Câu 16: Cho số thực x thỏa mãn Tính giá trị của 
	A. 	B. 	C. 	D. 
Câu 17: Cho hàm số có đồ thị (C) . Mệnh đề nào dưới đây là đúng. 
	A. (C) không có tiệm cận ngang	B.(C) có đúng một tiệm cận ngang 
 	C.(C) có đúng một tiệm cận ngang 	D. (C) có hai tiệm cận ngang và 
Câu 18: Trong không gian với hệ trục tọa độ, cho ba điểm Viết phương trình mặt thẳng qua A và vuông góc với đường thẳng BC.
	A. 	B. 
	C. 	D. 
Câu 19: Trong không gian với hệ trục toạ độ Oxyz, cho ba điểm và Viết phương trình đường trung tuyến đỉnh A của tam giác ABC.
	A. 	B. 
	C. 	D. 
Câu 20: Cho hàm số có bảng biến thiên. 
x
-1
0
1 
y’
-
0 +
+
0 -
y
2 
 -1
-1
3
 2
Hỏi hàm số có bao nhiêu cực trị?
A. . Có một điểm.	B. Có hai điểm.	C. Có ba điểm.	D. Có bốn điểm.
Đáp án
1-C
2-B
3-A
4-B
5-D
6-C
7-D
8-D
9-D
10-C
11-C
12-C
13-A
14-A
15-B
16-D
17-D
18-B
19-B
20-B
21-B
22-A
23-D
24-B
25-B
26-A
27-C
28-C
29-A
30-D
31-A
32-D
33-B
34-A
35-C
36-B
37-B
38-C
39-C
40-A
41-B
42-B
43-D
44-A
45-B
46-C
47-B
48-C
49-B
50-B
LỜI GIẢI CHI TIẾT
Câu 40: Đáp án A
Câu 41: Đáp án B
Đồ thị hàm số đã cho có 3 cực trị Phương trình có 3 nghiệm phân biệt . Khi đó 3 điểm cực trị của đồ thị là 
Gọi H là trung điểm . Ta có cân tại A. Do đó vuông khi và chỉ khi (do )
Câu 42: Đáp án B
Phương pháp: iết phương trình mặt phẳng (P) chứa M và 
Tìm B là giao của (P) và 
Tìm A là giao MB và 
Cách giải: Có là VTCP của 
Phương trình (P) chứa M và 
Giao của (P) và là 
Gọi thì 
M, A, B thẳng hàng 
Câu 43: Đáp án D
Phương pháp: Đặt ẩn phụ và tìm điều kiện chính xác cho ẩn phụ. 
Đưa phương trình đã cho về ẩn phụ để biện luận
Cách giải: đặt , phương trình đã cho trở thành 
Với ta tìm được 1 giá trị của x
Với ta tìm được 2 giá trị của x
Do đó, phương trình đã cho có 4 nghiệm phân biệt Phương trình (*) có 2 nghiệm phân biệt lớn hơn 1
Câu 44: Đáp án A
Thể tích của phần hình trụ là 
Thể tích phần hình nón cụt là hiệu thể tích của 2 hình nón, hình nón lớn có bán kính đáy 2cm, chiều cao 4cm và hình nón nhỏ có bán kính đáy 1cm, chiều cao 2cm, do đó thể tích phần hình nón cụt là 
Câu 45: Đáp án B
Phương pháp: Trong các hình chóp tam giác đều ngoại tiếp một mặt cầu, hình tứ diện đều có thể tích nhỏ nhất 
Cách giải: Áp dụng các công thức trong tứ diện đều cạnh a. 
Bán kính mặt cầu nội tiếp 
Thể tích tứ diện đều đó là 
Câu 46: Đáp án C
Phương pháp: Gọi phương trình mặt phẳng (P) đi qua M
Lập công thức tính thể tích OABC
Dùng bất đẳng thức để tìm giá trị nhỏ nhất
Cách giải: Gọi là 1 VTPT của (P). Để (P) cắt các tia Ox, Oy, Oz thì 
Phương trình mặt phẳng (P) đi qua M có dạng 
Khi đó ta có 
Vì OABC là tứ diện vuông nên 
Áp dụng bất đẳng thức Côsi cho 3 số dương: 
Câu 47: Đáp án B
Bất đẳng thức đã cho tương đương với 
Do đó 
Câu 48: Đáp án C
Áp dụng bất đẳng thức ta có: 
Câu 49: Đáp án B
Ta chứng minh được vuông tại E và . Ta có 
 vuông tại C có nên 
 vuông cân tại C nên 
 vuông tại E nên 
Suy ra 
Câu 50: Đáp án B
Thể tích của khối (H) được chia thành thể tích của rất nhiều lát mỏng hình vuông song song với hình vuông đáy của (H).
Lát mỏng hình vuông có độ cao x thì có cạnh là do đó có diện tích là 
Lấy tổng tất cả thể tích của những “lát mỏng” này ta được thể tích hình (H):