20 câu hỏi trắc nghiệm luyện thi Toán 12

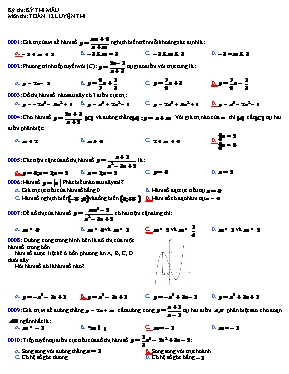
Kỳ thi: KỲ THI MẪU
Môn thi: TOÁN 12 LUYỆN THI
0001: Giá trị của m để hàm số nghịch biến trên mỗi khoảng xác định là:
A. .	B. 	C. 	D. 
0002: Phương trình tiếp tuyến với (C): tại giao điểm với trục tung là:
A. 	B. 	C. 	D. 
0003: Đồ thị hàm số nào sau đây có 3 điểm cực trị:
A. 	B. 	C. 	D. 
0004: Cho hàm số và đường thẳng. Với giá trị nào của thì cắt tại hai điểm phân biệt:
A. 	B. 	C. 	D. 
0005: Các tiệm cận của đồ thị hàm số là:
A. 	B. 	C. 	D. 
0006: Hàm số . Phát biểu nào sau đây sai?
A. Giá trị cực tiểu của hàm số bằng 0	B. Hàm số đạt cực tiểu tại 
C. Hàm số nghịch biếnvà đồng biến 	D. Hàm số có đạo hàm tại
0007: Để đồ thị của hàm số có hai tiệm cận đứng thì:
A. 	B. và 	C. và 	D. và 
0008: Đường cong trong hình bên là đồ thị của một hàm số trong bốn 
hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. 
Hỏi hàm số đó là hàm số nào ?
A. 	B. 	C. 	D. 
0009: Giá trị m để đường thẳng cắt đường cong tại hai điểm phân biệt sao cho đoạn ngắn nhất là:
A. 	B. 	C. 	D. 
0010: Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số :
A. Song song với đường thẳng .	B. Song song với trục hoành.
C. Có hệ số góc dương.	D. Có hệ số góc bằng .
0011: Cho hình chóp đều có cạnh đáy , góc giữa mặt bên và mặt đáy bằng . Tính thể tích của hình chóp.
A. 	B. 	C. 	D. 
0012: Cho hình chóp tứ giác có đáy là hình vuông cạnh và Thể tích của mặt cầu ngoại tiếp hình chóp là:
A. 	B. 	C. 	D. 
0013: Cho hình chóp có và cùng vuông góc , đường cao là
A. 	B. 	C. 	D. 
0014: Cho một hình đa diện. Tìm khẳng định sai trong các khẳng định sau:
A. Mỗi đỉnh là đỉnh chung của ít nhất ba cạnh	B. Mỗi đỉnh là đỉnh chung của ít nhất ba mặt
C. Mỗi cạnh là cạnh chung của ít nhất ba mặt	D. Mỗi mặt có ít nhất ba cạnh
0015: Có thể chia hình lập phương thành bao biêu tứ diện bằng nhau?
A. Hai	B. Vô số	C. Bốn	D. Sáu
0016: Cho hình chóp có đáy là hình bình hành với . vuông góc với đáy, góc giữa và mặt phẳng đáy là . Thể tích khối chóp là . Tỷ số là:
A. 4	B. 7	C. 5	D. 6
0017: Trong các hàm số sau, hàm số nào Không là hàm số luỹ thừa ?
A. Hàm số .	B. Hàm số .	C. Hàm số .	D. Hàm số .
0018: Tập xác định của hàm số là :
A. .	B. .	C. .	D. 
0019: Tìm để hàm số có cực đại, cực tiểu 
A. 	B. 	C. 	D. 
0020: Gọi có tung độ bằng . Tiếp tuyến của tại M cắt các trục tọa độ lần lượt tại A và B. Hãy tính diện tích tam giác ?
A. 	B. 	C. 	D.