Ứng dụng phương pháp lượng giác hóa

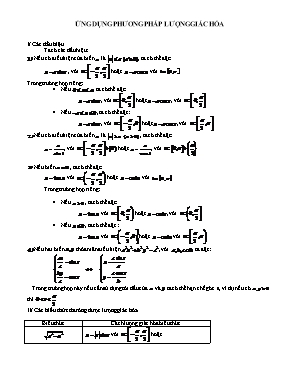
ỨNG DỤNG PHƯƠNG PHÁP LƯỢNG GIÁC HÓA
I/ Các dấu hiệu
	Ta có các dấu hiệu:
 Nếu có điều kiện của biến là , ta có thể đặt:
	 , với hoặc , với .
Trong trường hợp riêng:
Nếu , ta có thể đặt:
	, với hoặc, với .
Nếu , ta có thể đặt :
	, với hoặc, với .
Nếu có điều kiện của biến là , ta có thể đặt:
	, với hoặc , với .
Nếu biến , ta có thể đặt:
	, với hoặc , với .
	Trong trường hợp riêng:
Nếu , ta có thể đặt:
	, với hoặc , với .
Nếu , ta có thể đặt :
	, với hoặc ,với .
Nếu hai biến thỏa mãn điều kiện , với , ta đặt :
 Trong trường hợp này nếu cần sử dụng tới dấu của và ta có thể hạn chế góc , ví dụ nếu có thì .
II/ Các biểu thức thường được lượng giác hóa
Biểu thức
Cách lượng giác hóa biểu thức
 với hoặc
 với 
 với hoặc
 với 
 với hoặc
 với 
 hoặc 
 , với 
III/ Các ví dụ
1. Phương trình, hệ phương trình, bất phương trình
1.1 Bài toán 1: Giải hệ phương trình:
Lời giải
Hệ tương đương với. 
Nếu vô lí; vô lí.
Đặt ;	; . Ta có
; ; 
Khi đó: 	
Thay vào (4):	
Ta có các trường hợp sau:
Nếu	
Nếu	
Nếu	
Nếu	
1.2 Bài toán 2: Cho hệ phương trình
Tìm nghiệm của hệ để max
Lời giải
Đặt ; ; ; 	. Khi đó:
Mà	
	vì 
Khi đó: 
Kết hợp với (1) nghiệm là:
Kết hợp với (2) nghiệm là:
1.3 Bài toán 3: Giải phương trình:
Lời giải
Ta có :( phần CM xin để cho các bạn)
Do đó 
Vậy phương trình đã cho tương đường với 
1.4 Bài toán 4: Giải phương trình
Lời giải
Ta có
Do đó phương trình đã cho tương đương với hệ:
1.5 Các bài toán tự giải:
1.5.1 Giải phương trình
1.5.2 Giải hệ phương trình
1.5.3 Giải hệ phương trình
1.5.4 Giải hệ phương trình
1.5.5 Giải hệ phương trình
2. Bất đẳng thức
2.1 Bài toán 1: Cho bốn số thoã mãn điều kiện 
Chứng minh rằng
Lời giải 
Đặt và .
Ta có 
Vậy (điều phải chứng minh)
2.2 Bài toán 2: Chứng minh rằng
Lời giải
Điều kiện có nghĩa 
Đặt với 
Bất đẳng thức cần chứng minh có dạng
2.3 Các bài toán tự giải
2.3.1 Bài toán 1: Cho . Chứng minh rằng
2.3.2 Bài toán 2: Cho các số thoả mãn 
Chứng minh rằng
2.3.3 Bài toán 3: Cho liên hệ bởi 
Chứng minh rằng 	
3. Chứng minh đẳng thức
3.1 Bài toán 1: Cho thoả mãn điều kiện sau 	(1)
Chứng minh rằng
Lời giải
Đặt , , với 
Khi đó (1) có dạng
Do nên hay 
Vì nên . Vậy
Ta có
Tương tự
Suy ra
3.2 Bài toán 2: Cho thoả mãn 
Chứng minh rằng
Lời giải 
Đặt , , với 
Do nên
Do mà nên 
Vậy . Ta có
Tương tự ta có
Khi đó vế trái của đẳng thức cần chứng minh bằng
Suy ra điều phải chứng minh
3.3 Các bài toán tự giải
3.3.1 Bài toán 1:Cho . Chứng minh rằng:
3.3.2 Bài toán 2: Cho và thoả điều kiện 
Chứng minh rằng 
3.3.3 Bài toán 3: Cho và 
Chứng minh rằng