Tuyển tập đề thi vào Lớp 10 các trường chuyên - năng khiếu môn Tiếng Anh - Năm học 2013-2014

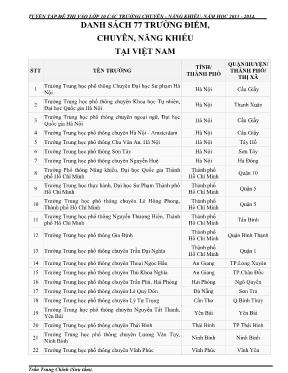
TUYỂN TẬP ĐỀ THI VÀO LỚP 10 CÁC TRƯỜNG CHUYÊN - NĂNG KHIẾU, NĂM HỌC 2013 - 2014. 
Trần Trung Chính (Sưu tầm). 
DANH SÁCH 77 TRƯỜNG ĐIỂM, 
CHUYÊN, NĂNG KHIẾU 
TẠI VIỆT NAM 
STT TÊN TRƯỜNG 
TỈNH/ 
THÀNH PHỐ 
QUẬN/HUYỆN/ 
THÀNH PHỐ/ 
THỊ XÃ 
1 
Trường Trung học phổ thông Chuyên Đại học Sư phạm Hà 
Nội 
Hà Nội Cầu Giấy 
2 
Trường Trung học phổ thông chuyên Khoa học Tự nhiên, 
Đại học Quốc gia Hà Nội 
Hà Nội Thanh Xuân 
3 
Trường Trung học phổ thông chuyên ngoại ngữ, Đại học 
Quốc gia Hà Nội 
Hà Nội Cầu Giấy 
4 Trường Trung học phổ thông chuyên Hà Nội - Amsterdam Hà Nội Cầu Giấy 
5 Trường Trung học phổ thông Chu Văn An, Hà Nội Hà Nội Tây Hồ 
6 Trường Trung học phổ thông Sơn Tây Hà Nội Sơn Tây 
7 Trường Trung học phổ thông chuyên Nguyễn Huệ Hà Nội Hà Đông 
8 
Trường Phổ thông Năng khiếu, Đại học Quốc gia Thành 
phố Hồ Chí Minh 
Thành phố 
Hồ Chí Minh 
Quận 10 
9 
Trường Trung học thực hành, Đại học Sư Phạm Thành phố 
Hồ Chí Minh 
Thành phố 
Hồ Chí Minh 
Quận 5 
10 
Trường Trung học phổ thông chuyên Lê Hồng Phong, 
Thành phố Hồ Chí Minh 
Thành phố 
Hồ Chí Minh 
Quận 5 
11 
Trường Trung học phổ thông Nguyễn Thượng Hiền, Thành 
phố Hồ Chí Minh 
Thành phố 
Hồ Chí Minh 
Tân Bình 
12 Trường Trung học phổ thông Gia Định 
Thành phố 
Hồ Chí Minh 
Quận Bình Thạnh 
13 Trường Trung học phổ thông chuyên Trần Đại Nghĩa 
Thành phố 
Hồ Chí Minh 
Quận 1 
14 Trường Trung học phổ thông chuyên Thoại Ngọc Hầu An Giang TP.Long Xuyên 
15 Trường Trung học phổ thông chuyên Thủ Khoa Nghĩa An Giang TP.Châu Đốc 
16 Trường Trung học phổ thông chuyên Trần Phú, Hải Phòng Hải Phòng Ngô Quyền 
17 Trường Trung học phổ thông chuyên Lê Quý Đôn Đà Nẵng Sơn Trà 
18 Trường Trung học phổ thông chuyên Lý Tự Trọng Cần Thơ Q.Bình Thủy 
19 
Trường Trung học phổ thông chuyên Nguyễn Tất Thành, 
Yên Bái 
Yên Bái Yên Bái 
20 Trường Trung học phổ thông chuyên Thái Bình Thái Bình TP Thái Bình 
21 
Trường Trung học phổ thông chuyên Lương Văn Tụy, 
Ninh Bình 
Ninh Bình Ninh Bình 
22 Trường Trung học phổ thông chuyên Vĩnh Phúc Vĩnh Phúc Vĩnh Yên 
TUYỂN TẬP ĐỀ THI VÀO LỚP 10 CÁC TRƯỜNG CHUYÊN - NĂNG KHIẾU, NĂM HỌC 2013 - 2014. 
Trần Trung Chính (Sưu tầm). 
23 Trường Trung học phổ thông chuyên Bắc Giang Bắc Giang TP Bắc Giang 
24 Trường Trung học phổ thông chuyên Bắc Kạn Bắc Kạn Bắc Kạn 
25 Trường Trung học phổ thông chuyên Bắc Ninh Bắc Ninh Bắc Ninh 
26 Trường Trung học phổ thông chuyên Cao Bằng Cao Bằng Cao Bằng 
27 Trường Trung học phổ thông chuyên Nguyễn Trãi Hải Dương TP Hải Dương 
28 Trường Trung học phổ thông chuyên Lào Cai Lào Cai 
Lào Cai 
(thành phố) 
29 Trường Trung học phổ thông chuyên Hoàng Văn Thụ Hòa Bình 
Hòa Bình 
(thành phố) 
30 Trường Trung học phổ thông chuyên Tuyên Quang Tuyên Quang 
Tuyên Quang 
(thành phố) 
31 Trường Trung học phổ thông chuyên Hà Giang Hà Giang 
Hà Giang 
(thành phố) 
32 Trường Trung học phổ thông chuyên Chu Văn An Lạng Sơn 
Lạng Sơn 
(thành phố) 
33 Trường Trung học phổ thông chuyên Lê Quý Đôn Điện Biên Điện Biên Phủ 
34 Trường Trung học phổ thông chuyên Lê Quý Đôn Lai Châu 
Lai Châu 
(thị xã) 
35 Trường Trung học phổ thông chuyên Sơn La Sơn La 
Sơn La 
(thành phố) 
36 Trường Trung học phổ thông chuyên Thái Nguyên Thái Nguyên P.Quang Trung 
37 
Trường Trung học phổ thông chuyên Hùng Vương, Phú 
Thọ 
Phú Thọ Việt Trì 
38 
Trường Trung học phổ thông chuyên Lê Hồng Phong, Nam 
Định 
Nam Định Nam Định 
39 Trường Trung học phổ thông chuyên Biên Hòa Hà Nam Phủ Lý 
40 Trường Trung học phổ thông chuyên Hạ Long Quảng Ninh TP Hạ Long 
41 Trường Trung học phổ thông chuyên Hưng Yên Hưng Yên Hưng Yên 
42 Trường Trung học phổ thông chuyên Lam Sơn, Thanh Hóa Thanh Hóa Thanh Hóa 
43 
Trường Trung học phổ thông chuyên Phan Bội Châu, Nghệ 
An 
Nghệ An Vinh 
44 
Trường Trung học phổ thông chuyên, Trường Đại học 
Vinh, Nghệ An 
Nghệ An Vinh 
45 Trường Trung học phổ thông chuyên Hà Tĩnh Hà Tĩnh Hà Tĩnh 
46 Trường Trung học phổ thông chuyên Quảng Bình Quảng Bình Đồng Hới 
47 
Trường Trung học phổ thông chuyên Lê Quý Đôn, Quảng 
Trị 
Quảng Trị Đông Hà 
48 Quốc Học Huế Thừa Thiên-Huế Huế 
49 Trường Trung học phổ thông chuyên Bắc Quảng Nam Quảng Nam Hội An 
50 Trường Trung học phổ thông chuyên Nguyễn Bỉnh Khiêm Quảng Nam Tam Kỳ 
www.VNMATH.com
TUYỂN TẬP ĐỀ THI VÀO LỚP 10 CÁC TRƯỜNG CHUYÊN - NĂNG KHIẾU, NĂM HỌC 2013 - 2014. 
Trần Trung Chính (Sưu tầm). 
51 Trường Trung học phổ thông chuyên Lê Khiết Quảng Ngãi 
Quảng Ngãi 
(thành phố) 
52 
Trường Trung học phổ thông chuyên Lê Quý Đôn, Bình 
Định 
Bình Định Quy Nhơn 
53 Trường Trung học phổ thông chuyên Lương Văn Chánh Phú Yên Tuy Hòa 
54 
Trường Trung học phổ thông chuyên Lê Quý Đôn, Khánh 
Hòa 
Khánh Hòa Nha Trang 
55 
Trường Trung học phổ thông chuyên Lê Quý Đôn, Ninh 
Thuận 
Ninh Thuận 
Phan Rang - 
Tháp Chàm 
56 
Trường Trung học phổ thông chuyên Trần Hưng Đạo, Bình 
Thuận 
Bình Thuận Phan Thiết 
57 Trường Trung học phổ thông chuyên Thăng Long - Đà Lạt Lâm Đồng TP. Đà Lạt 
58 Trường Trung học phổ thông chuyên Nguyễn Du, Đắk Lắk Đắk Lắk Buôn Ma Thuột 
59 Trường Trung học phổ thông chuyên Hùng Vương Gia Lai Pleiku 
60 
Trường Trung học phổ thông chuyên Nguyễn Tất Thành, 
Kon Tum 
Kon Tum 
Kon Tum 
(thành phố) 
61 
Trường Trung học phổ thông chuyên Lương Thế Vinh, 
Đồng Nai 
Đồng Nai Biên Hòa 
62 
Trường Trung học phổ thông chuyên Lê Quý Đôn, Vũng 
Tàu 
Bà Rịa - Vũng 
Tàu 
Vũng Tàu 
63 Trường Trung học phổ thông chuyên Bến Tre Bến Tre Bến Tre 
64 
Trường Trung học Phổ thông Chuyên Quang Trung, Bình 
Phước 
Bình Phước Đồng Xoài 
65 Trường Trung học phổ thông chuyên Tiền Giang Tiền Giang Mỹ Tho 
66 Trường Trung học phổ thông chuyên Vị Thanh Hậu Giang Vị Thanh 
67 Trường Trung học phổ thông chuyên Bạc Liêu Bạc Liêu 
Bạc Liêu 
(thành phố) 
68 Trường Trung học phổ thông chuyên Phan Ngọc Hiển Cà Mau Cà Mau 
69 Trường Trung học phổ thông chuyên Hùng Vương Bình Dương Thủ Dầu Một 
70 Trường Trung học phổ thông chuyên Huỳnh Mẫn Đạt Kiên Giang Rạch Giá 
71 Trường Trung học phổ thông chuyên Nguyễn Bỉnh Khiêm Vĩnh Long Vĩnh Long 
72 Trường Trung học phổ thông chuyên Trà Vinh Trà Vinh 
Trà Vinh 
(thành phố) 
73 Trường Trung học phổ thông chuyên Hoàng Lệ Kha Tây Ninh 
Tây Ninh 
(thị xã) 
74 
Trường Trung học phổ thông chuyên Nguyễn Thị Minh 
Khai 
Sóc Trăng 
Sóc Trăng 
(thành phố) 
75 Trường Trung học phổ thông chuyên Nguyễn Quang Diêu Đồng Tháp 
Cao Lãnh 
(thành phố) 
76 Trường Trung học phổ thông chuyên Nguyễn Đình Chiểu Đồng Tháp Sa Đéc (thị xã) 
77 Trường Trung học phổ thông chuyên Long An Long An Tân An 
TUYỂN TẬP ĐỀ THI VÀO LỚP 10 CÁC TRƯỜNG CHUYÊN - NĂNG KHIẾU, NĂM HỌC 2013 - 2014. 
Trần Trung Chính (Sưu tầm). 
ĐỀ SỐ 1 
SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI TUYỂN SINH VÀO LỚP 10 
 TRƯỜNG ĐHSP HÀ NỘI TRƯỜNG THPT CHUYÊN ĐẠI HỌC SƯ PHẠM HÀ NỘI 
 NĂM HỌC 2013 - 2014 
 ĐỀ CHÍNH THỨC 
VÒNG 1 
Môn: Toán 
Thời gian làm bài: 120 phút. 
Không kể thời gian giao đề 
Câu 1: (2,5 điểm) 
 1. Cho biểu thức: 
3
2
a b
2a a b b
ab aa b
Q
3a 3b ab a a b a
 
     
 
 với a > 0, b > 0, a ≠ b. Chứng minh giá trị của biểu thức Q không phụ thuộc vào a và b. 
 2. Các số thức a, b, c thỏa mãn a + b + c = 0. 
 Chứng minh đẳng thức:    
2
2 2 2 4 4 4a b c 2 a b c     . 
Câu 2: (2,0 điểm) 
 Cho parabol (P): y = x
2
 và đường thẳng (d): 
2
1
y mx
2m
   (tham số m ≠ 0) 
 1. Chứng minh rằng với mỗi m ≠ 0, đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt. 
 2. Gọi    1 1 2 2A x ; y , B x ; y là các giao điểm của (d) và (P). 
 Tìm giá trị nhỏ nhất của biểu thức: 2 21 2M y y  . 
Câu 3: (1,5 điểm) 
 Giả sử a, b, c là các số thực, a ≠ b sao cho hai phương trình: x2 + ax + 1 = 0, x2 + bx + 1 = 0 có 
 nghiệm chung và hai phương trình x2 + x + a = 0, x2 + cx + b = 0 có nghiệm chung. 
 Tính: a + b + c. 
Câu 4: (3,0 điểm) 
 Cho tam giác ABC không cân, có ba góc nhọn, nội tiếp đường tròn (O). Các đường cao AA1, 
 BB1, C C1 của tam giác ABC cắt nhau tại H, các đường thẳng A1C1 và AC cắt nhau tại điểm D. 
 Gọi X là giao điểm thứ hai của đường thẳng BD với đường tròn (O). 
 1. Chứng minh: DX.DB = DC1.DA1. 
 2. Gọi M là trung điểm của cạnh AC. Chứng minh: DH  BM. 
Câu 5: (1,0 điểm) 
 Các số thực x, y, x thỏa mãn: 
x 2011 y 2012 z 2013 y 2011 z 2012 x 2013
y 2011 z 2012 x 2013 z 2011 x 2012 y 2013
           

          
 Chứng minh: x = y = z. 
............. Hết ............. 
Họ và tên thí sinh: ............................................................ Số báo danh: ........................... 
Ghi chú: Cán bộ coi thi không giải thích gì thêm! 
www.VNMATH.com
TUYỂN TẬP ĐỀ THI VÀO LỚP 10 CÁC TRƯỜNG CHUYÊN - NĂNG KHIẾU, NĂM HỌC 2013 - 2014. 
Trần Trung Chính (Sưu tầm). 
SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI TUYỂN SINH VÀO LỚP 10 
 TRƯỜNG ĐHSP HÀ NỘI TRƯỜNG THPT CHUYÊN ĐẠI HỌC SƯ PHẠM HÀ NỘI 
 NĂM HỌC 2013 - 2014 
 ĐỀ CHÍNH THỨC 
VÒNG 2 
Môn: Toán 
Thời gian làm bài: 150 phút. 
Không kể thời gian giao đề 
Câu 1: (2,5 điểm) 
 1. Các số thực a, b, c thỏa mãn đồng thời hai đẳng thức: 
 i) (a + b)(b + c)(c + a) = abc 
 ii) (a
3
 + b
3
)(b
3
 + c
3
)(c
3
 + a
3
) = a
3
b
3
c
3
 Chứng minh: abc = 0. 
 2. Các số thực dương a, b thỏa mãn ab > 2013a + 2014b. Chứng minh đẳng thức: 
 
2
a b 2013 2014   
Câu 2: (2,0 điểm) 
 Tìm tất cả các cặp số hữu tỷ (x; y) thỏa mãn hệ phương trình: 
3 3
2 2
x 2y x 4y
6x 19xy 15y 1
   

  
Câu 3: (1,0 điểm) 
 Với mỗi số nguyên dương n, ký hiệu Sn là tổng của n số nguyên tố đầu tiên. 
S1 = 2, S2 = 2 + 3, S3 = 2 + 3 + 5, ...) 
 Chứng minh rằng trong dãy số S1, S2, S3, ... không tồn tại hai số hạng liên tiếp đều là số chính 
 phương. 
Câu 4: (2,5 điểm) 
 Cho tam giác ABC không cân, nội tiếp đường tròn (O), BD là đường phân giác của góc ABC. 
 Đường thẳng BD cắt đường tròn (O) tại điểm thứ hai là E. Đường tròn (O1) đường kính DE cắt 
 đường tròn (O) tại điểm thứ hai là F. 
 1. Chứng minh rằng đường thẳng đối xứng với đường thẳng BF qua đường thẳng BD đi qua 
 trung điểm của cạnh AC. 
 2. Biết tam giác ABC vuông tại B,  0BAC 60 và bán kính của đường tròn (O) bằng R. Hãy 
 tính bán kính của đường tròn (O1) theo R. 
Câu 5: (1,0 điểm) 
 Độ dài ba cạnh của tam giác ABC là ba số nguyên tố. Chứng minh minh rằng diện tích của tam 
 giác ABC không thể là số nguyên. 
Câu 6: (1,0 điểm) 
 Giả sử a1, a2, ..., a11 là các số nguyên dương lớn hơn hay bằng 2, đôi một khác nhau và thỏa 
 mãn: 
a1 + a2 + ... + a11 = 407 
 Tồn tại hay không số nguyên dương n sao cho tổng các số dư của các phép chia n cho 22 số 
 a1, a2 , ..., a11, 4a1, 4a2, ..., 4a11 bằng 2012. 
............. Hết ............. 
Họ và tên thí sinh: ............................................................ Số báo danh: ........................... 
Ghi chú: Cán bộ coi thi không giải thích gì thêm! 
TUYỂN TẬP ĐỀ THI VÀO LỚP 10 CÁC TRƯỜNG CHUYÊN - NĂNG KHIẾU, NĂM HỌC 2013 - 2014. 
Trần Trung Chính (Sưu tầm). 
ĐÁP ÁN MÔN TOÁN (vòng 2) 
ĐỀ THI VÀO LỚP 10 TRƯỜNG THPT CHUYÊN ĐHSP HÀ NỘI 
NĂM HỌC 2013 - 2014 
Câu 1: 
1. 
Từ ii) suy ra: (a + b)(b + c)(c + a)(a2 - ab + b2)(b2 - bc + c2)(c2 - ca + a2) = a3b3c3. 
Kết hợp với i) suy ra: abc(a2 - ab + b2)(b2 - bc + c2)(c2 - ca + a2) = a3b3c3. 
     2 2 2 2 2 2 3 3 3
abc 0
a ab b b bc c c ca a a b c 1

 
      
Nếu abc ≠ 0 thì từ các bất đẳng thức 
2 2
2 2
2 2
a ab b ab
b bc c bc
c ca a ca
   

  

  
Suy ra: (a
2
 - ab + b
2
)(b
2
 - bc + c
2
)(c
2
 - ca + a
2) ≥ a2b2c2, kết hợp với (1) suy ra: a = b = c. 
Do đó: 8a3 = 0  a = 0  abc = 0 (mẫu thuẫn). Vậy abc = 0. 
2. 
Từ giả thiết suy ra: 
2013 2014
1
b a
  
   
 
2
2013 2014
a b a b a b
b a
2013a 2014 2013a 2014b
2013 2014 2013 2 . 2014 2013 2014
b a b a
     
        
Câu 2: 
Nếu x = 0 thay vào hệ ta được: 
3
2
2y 4y
15y 1
 


 hệ này vô nghiệm. 
Nếu x ≠ 0, đặt y = tx, hệ trở thành 
 
 
2 33 3 3
2 2 2 2 2 2
x 1 2t 1 4tx 2t x x 4tx
6x 19tx 15t x 1 x 15t 19t 6 1
       
 
      
Suy ra: 3 21 2t 0;15t 19t 6 0     và 3 2
3 2
1 4t 1
62t 61t 5t 5 0
1 2t 15t 19t 6

     
  
  
 
22t 1 31t 15t 5 0
2t 1 0
1
t Do t Q .
2
    
  
  
Suy ra: 2x 4 x 2 y 1       
Đáp số: (2; 1), (-2, -1). 
Câu 3: 
Ký hiệu pn là số nguyên tố thứ n. 
Giả sử tồn tại m mà Sm-1 = k
2
; Sm = l
2
; k, l N*. 
Vì S2 = 5, S3 = 10, S4 = 17  m > 4. 
Ta có: pm = Sm - Sm-1 = (l - k)(l + k). 
Vì pm là số nguyên tố và k + l > 1 nên 
m
l k 1
l k p
 

 
www.VNMATH.com
TUYỂN TẬP ĐỀ THI VÀO LỚP 10 CÁC TRƯỜNG CHUYÊN - NĂNG KHIẾU, NĂM HỌC 2013 - 2014. 
Trần Trung Chính (Sưu tầm). 
Suy ra: 
2
m
m m m
p 1
p 2l 1 2 S 1 S
2
 
       
 
 (1) 
Do m > 4 nên 
 m m
2 2 2 2
2 2 2 2 2 2 m m m m
S 1 3 5 7 ... p 2 1 9
p 1 p 1 p 1 p 1
 1 0 2 1 3 2 ... 8 8
2 2 2 2
        
           
                    
         
(mâu thuẫn với (1)). 
Câu 4: 
1. 
Gọi M là trung điểm của cạnh AC. 
Do E là điểm chính giữa của cung AC nên EM  AC. 
Suy ra: EM đi qua tâm của đường tròn (O). 
Dọi G là giao điểm của DF với (O). 
Do  0DFE 90 . Suy ra: GE là đường kính của (O). 
Suy ra: G, M, E thẳng hàng. 
Suy ra:  0GBE 90 , mà  0GMD 90 . Suy ra tứ giác 
BDMG là tứ giác nội tiếp đường tròn đường kính GD. 
 MBD FBE  . 
Suy ra: BF và BM đối xứng với nhau qua BD. 
2. 
Từ giả thiết suy ra M là tâm đường tròn ngoại tiếp tam 
giác ABC và AB =R, BC = R 3 . 
Theo tính chất đường phân giác: 
DA R 1
DC 3DA
DC R 3 3
    . 
Kết hợp với DA = DC = 2R. 
Suy ra:     2 2DA 3 1 R DM R DA 2 3 R DE ME MD 2 2 3R            
Vậy bán kính đường tròn (O1) bằng 2 3R . 
Câu 5: 
Giả sử a; b; c là các số nguyên tố và là độ dài các cạnh của tam giác ABC. 
Đặt: P = a + b + c, ký hiệu S là diện tích của tam giác ABC. 
Ta có: 16S
2
 = P(P - 2a)(P - 2b)(P - 2c) (1) 
Giả sử S là số tự nhiên. Từ (1) suy ra: P = a + b + c chẵn. 
Trường hợp 1: Nếu a; b; c cùng chẵn thì a = b = c, suy ra: S = 3 (loại) 
Trường hợp 2: Nếu a; b; c có một số chẵn và hai số lẻ, giả sử a chẵn thì a = 2. 
Nếu b ≠ c  |b - c| ≥ 2 = a, vô lý. 
Nếu b = c thì S2 = b2 - 1  (b - S)(b + S) = 1 (2) 
Đẳng thức (2) không xảy ra vì b; S là các số tự nhiện. 
Vậy diện tích của tam giác ABC không thể là số nguyên. 
Câu 6: 
Ta chứng minh không tồn tại n thỏa mãn đề bài. 
Giả sử ngược lại, tồn tại n, ta luôn có: 
Tổng các số dư trong phép chia n cho a1, a2, ..., a11 không thể vượt quá 407 - 11 = 396. 
Tổng các số dư trong phép chia n cho các số 4a1, 4a2, ..., 4a11 không vượt quá 4.407 - 11 = 1617. 
Suy ra: Tổng các số dư trong phép chia n cho các số a1, a2, ..., a11, 4a1, 4a2, ..., 4a11 không thể vượt quá 
396 + 1617 = 2013. 
M
G
F E
D
O
C
B
A
TUYỂN TẬP ĐỀ THI VÀO LỚP 10 CÁC TRƯỜNG CHUYÊN - NĂNG KHIẾU, NĂM HỌC 2013 - 2014. 
Trần Trung Chính (Sưu tầm). 
Kết hợp với giả thiết tổng các số dư bằng 2012. 
Suy ra khi chia n cho 22 số trên thì có 21 phép chia có số dư lớn nhất và một phép chia có số dư nhỏ 
hơn số chia 2 đơn vị. 
Suy ra: Tồn tại k sao cho ak, 4ak thỏa mãn điều kiện trên. 
Khi đó một trong hai số n + 1; n + 2 chia hết cho ak, số còn lại chia hết cho 4ak. 
Suy ra: (n + 1; n + 2) ≥ ak ≥ 2, điều này không đúng. 
Vậy không tồn tại n thỏa mãn đề ra. 
----- HẾT ----- 
www.VNMATH.com
TUYỂN TẬP ĐỀ THI VÀO LỚP 10 CÁC TRƯỜNG CHUYÊN - NĂNG KHIẾU, NĂM HỌC 2013 - 2014. 
Trần Trung Chính (Sưu tầm). 
ĐỀ SỐ 2 
SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI TUYỂN SINH VÀO LỚP 10 
 HÀ NỘI TRƯỜNG THPT CHUYÊN KHTN - ĐHQG HÀ NỘI 
 NĂM HỌC 2013 - 2014 
 ĐỀ CHÍNH THỨC 
Môn: Toán (vòng 1) 
Ngày thi: 08/06/2013 
Thời gian làm bài: 150 phút. 
Không kể thời gian giao đề 
Câu 1: 
 1. Giải phương trình: 3x 1 2 x 3    . 
 2. Giải hệ phương trình: 
1 1 9
x y
x y 2
1 3 1 1
x xy
4 2 y xy

   


        
Câu 2: 
 1. Giả sử a, b, c là các số thực khác 0 thỏa mãn đẳng thức (a + b)(b + c)(c + a) = 8abc. Chứng 
 minh rằng: 
        
a b c 3 ab bc ca
a b b c c a 4 a b b c b c c a c a a b
     
        
 2. Hỏi có bao nhiêu số nguyên dương có 5 chữ số abcde sao cho  abc 10d e  chia hết cho 
 101? 
Câu 3: Cho ABC nhọn nội tiếp đường tròn (O) với AB < AC. Đường phân giác của BAC cắt (O) tại 
 D ≠ A. Gọi M là trung điểm của AD và E là điểm đối xứng với D qua O. Giả dụ (ABM) cắt 
 AC tại F. Chứng minh rằng: 
 1) BDM ∽ BCF. 
 2) EF  AC. 
Câu 4: Giả sử a, b, c, d là các số thực dương thỏa mãn: abc + bcd + cad + bad = 1. 
 Tìm giá trị nhỏ nhất của: P = 4(a3 + b3 + c3) + 9d3. 
............. Hết ............. 
Họ và tên thí sinh: ............................................................ Số báo danh: ........................... 
Ghi chú: Cán bộ coi thi không giải thích gì thêm! 
TUYỂN TẬP ĐỀ THI VÀO LỚP 10 CÁC TRƯỜNG CHUYÊN - NĂNG KHIẾU, NĂM HỌC 2013 - 2014. 
Trần Trung Chính (Sưu tầm). 
ĐÁP ÁN MÔN TOÁN (vòng 1) 
ĐỀ THI VÀO LỚP 10 TRƯỜNG THPT CHUYÊN KHTN - ĐHQG HÀ NỘI 
NĂM HỌC 2013 - 2014 
Câu 1: 
1. Hướng dẫn: Đặt điều kiện, bình phương hai lần được phương trình bậc 2, nhận 2 nghiệm là 1, 
7
4
. 
2. Đặt: 
1 1 1 1 1
t x ; v y tu x y xy 2
y x y x xy
  
            
  
, ta có hệ phương trình: 
 
 
2
2
9
t u 2u 9 2t 2u 9 2t2t 2u 92
2t 9 2t 6t 9 01 3 4tu 6t 9 0 4t 126t 9 0
tu 2
4 2
u 32u 9 2t 2u 9 2t
3
2t 3 t2t 3 0
2

        
     
             

    
    
     
  2
1 3
x 3 3
y 2xy 2xxy y 1 0 y 3x 0y 2
2 2
x 1 2x 1 02x 3x 1 01
xy 3x 1 0 xy 3x 1 0y 3
x

             
        
                

x 1
y 2

 

 hoặc 
1
x
2
y 1



 
. 
Thử lại, ta thấy phương trình nhận hai nghiệm (x; y) là  
1
1; 2 ; ;1
2
 
 
 
. 
Câu 2: 
1. Khai triển và rút gọn (a + b)(b + c)(c + a) = 8abc. 
Ta được: a2b + b2a + b2c + c2b + c2a + a2c = 6abc. 
 
        
        
   
2 2 2 2 2 2
a ab b bc c ca 3
1
a b a b b c b c b c c a c a c a a b 4
ab ac ab bc ba bc ca cb ca 3
a b b c b c c a c a a b 4
a b b a b c c b c a a c 3
a b b c c a 4
6abc 3
8abc 4
      
        
     
   
     
    
 
  
 
Luôn luôn đúng. Suy ra: Điều phải chứng minh. 
2. Ta có: 
   abc 10d e 101 101.abc abc 10d d 101 100.abc 10d e 101 abcde 101.               
Vậy số các số phải tìm chính là số các số tự nhiên có 5 chữ số chia hết cho 101. 
10000 + 100 = 101 x 100  10100 là số các số tự nhiên có 5 chữ số nhỏ nhất chia hết cho 101. 
99999 – 9 = 101 x 990  99990 là số các số tự nhiên có 5 chữ số lớn nhất chia hết cho 101. 
Vậy số các số tự nhiên có 5 chữ số chia hết cho 101 là 
99990 10100
1 891
101

  số. 
Câu 3: 
www.VNMATH.com
TUYỂN TẬP ĐỀ THI VÀO LỚP 10 CÁC TRƯỜNG CHUYÊN - NĂNG KHIẾU, NĂM HỌC 2013 - 2014. 
Trần Trung Chính (Sưu tầm). 
1. Tứ giác AFMB nội tiếp  AFB AMB  . 
Mà    0 0AFB BEC 180 , AMB BMD 180    
 BMD BED  mà ABDC nội tiếp  1 1D C  
BDM ∽ BCF (g.g). 
Suy ra: Điều phải chứng minh. 
2. Do  1 2A A  (gt) 
Suy ra: D là điểm chính giữa cung BC. 
DO BC  tại trung điểm H của BC. 
BMD ∽ BFC 
1
DA
BD DM BD BD DA2 .
BC CF 2BH CF BH CF
      
Mà  1 2D C  (chứng minh trên) 
BDA ∽ HCF (c.g.c)  1 1F A  
Mà  1 2A A (gt) và 
 
2 1A E (cùng chắn mộtc ung DC). 
 
1 1F E  EFHC nội tiếp. 
Câu 4: Trước hết ta chứng minh với mọi x, y, y ≥ 0, ta có: x3 + y3 + z3 ≥ 3xyz. (*) 
Tự chứng minh 3 số hoặc phân tích thành nhân tử, các trường THPT chuyên tại TP HCM khôn