Toán học Tích phân luyên thi đại học

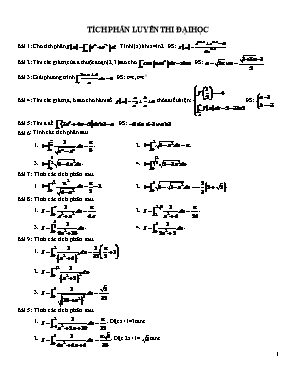
TÍCH PHÂN LUYÊN THI ĐẠI HỌC
Bài 1: Cho tích phân . Tính I(x) khi x=ln2. ĐS: .
Bài 2: Tìm các giá trị của a thuộc đoạn [2;3] sao cho . ĐS: .
Bài 3: Giải phương trình . ĐS: t=e, t=e-9
Bài 4: Tìm các giá trị a, b sao cho hàm số thỏa điều kiện: ĐS: .
Bài 5: Tìm a để . ĐS: .
Bài 6: Tính các tích phân sau. 
	1. .	2. .
3. .	4. .
Bài 7: Tính các tích phân sau.
1. . 	2. . 
Bài 8: Tính các tích phân sau.
	1. .	2. .
	3. .	4. .	 
Bài 9: Tính các tích phân sau.
1. . 
2. . 
3. . 
Bài 5: Tính các tích phân sau.
	1. . Đặt x+1=3tant. 
	2. . Đặt 2x+1=tant. 
	3. . Đặt x+=tant. 4. . 
Bài 6: Tính các tích phân sau.
1. . 	2. . 3. 
Bài 7: Tính các tích phân sau.
Bài 3: Tính các tích phân sau.
1. 	2. 	3. 
4. 	5. 
Bài 4: Tính các tích phân sau.
	1. 	
2. , chú ý: khi m>n. 
3. 	4. 	
5. 	6. 
7. 	8. 
9. 	10. 
Bài 5: Tính các tích phân sau.
	1. 	2. 
	3. 	4. 
	5. 	6. 
	7. Tìm A, B sao cho f(x)= thỏa . 
	8. Tìm A, B sao cho f(x)= thỏa . 
	9. Cho . Giải phương trình f(t)=0. ĐS: .
BÀI TẬP TÍCH PHÂN
	1/ . ĐS: HD: Làm cho mất mẫu số.
	2/ .
	3/ HD: Đổi biến thành đổi biến.
	4/ HD: Đổi biến thành đổi biến.
	5/ HD: Đổi biến thành đổi biến.
	6/ HD: Đổi biến thành biến đổi.
	7/ HD: Đổi biến.
	8/ . HD: Đổi biến.
	9/ . Có ba cách giải.
	10/ .
	11/ . Từng phần.
	12/ Cho . Giải phương trình f(t)=0. ĐS: .
	13/ Tìm A, B sao cho f(x)= thỏa . 
ĐS: 
	14/ Tìm A, B sao cho f(x)= thỏa . 
ĐS: 
	15/ Tìm các giá trị của hằng số a biết: ĐS: a=3.
	16/ 	17/ 	
 	18/ 	19/ 
BÀI TẬP TÍCH PHÂN
Cách 2: Đổi biến đặt t=x2+1
BÀI TẬP ÔN THI ĐẠI HỌC
Bài 1: Tính tích phân: 
	1. 	2. 
	3. 	4. . 
Bài 2: Tính tích phân: 
	1. 	2. 
	3. 	4. 
Bài 3: Tính tích phân:
	1. 	2. .
	3. 	4. 
Bài 4: Tính các tích phân sau: 
	1. 	2. .
Bài 5: Tính tích phân sau: 
	1. . Áp dụng hằng đẳng thức chia làm 2 tích phân.	
Cần nhớ: 
2. 
	3. 	
4. . Đặt x2 ra khỏi căn, đặt . 
Bài 6: Tính các tích phân. 
	1. . 	2. 
	3. 	4. 
Bài 7: Tính các tích phân. 
	1. . 	2. 
	3. 	4. 
Bài 8: Tính các tích phân. 
	1. . 	2. 
	3. 	4. 
Bài 9: Tính các tích phân. 
	1. . 	2. 
	3. 	4. 
Bài 10: Tính các tích phân. 
	1. . 	2. 
	3. 	4. 
Bài 11: Tính các tích phân. 
	1. . 	2. 
	3. 	
4. 
5. 	6. 
Bài 12: Tính các tích phân. 
	1. 	2. 
	3. 	4. 
	5. 	6. 
Bài 13: Tính các tích phân. 
	1. 	2. 
	3. 	4. 
	5. 	6. 
Bài 14: Tính các tích phân. 
	1. 	2. 
	3. 	4. 
	5. 	6. 
Bài 15: Tính các tích phân. 
	1. 	2. 
Bài 16: Tính các tích phân. 
	1. 	2. 
	3. I=	4. I=
	5. I=	6. I=
	7. 	8. I=
	9. I=	10. I=
	11. 	12. 
	13. 	14. 
	15. 	16. 
17. I = 	18. 
	21. 
22. 	23. 
24. 	24. I=
25. 	26. 
27. I=	28. 
29. I=	30. 
31. I=	`	32. I=
33. I=	34. I=
35. I=	36. I=
37. I=
TÍCH PHÂN HÀM HỮU TỶ - VÀ HÀM LƯỢNG GIÁC
Dạng 1: 
TH 1: Tam thức có nghiệm kép.
VD: Tính tích phân:
	1. 	2. 
	3. 	4. 
VD: Tính các tích phân sau: 
	1. 	2. 
	3. 	4. 
TH3: Tam thức vô nghiệm. 
VD: Tính các tích phân sau: Chú ý: u là một hàm số bậc nhất theo biến x, còn m là một số thực. 
	1. 	2. 
	3. 	4. 
Dạng 2: 
Cần nhớ: x0 là nghiệm kép, có thể mở mũ 3 hoặc 4
VD: Tính tích phân sau: 
	1. 	2. 	3. 
Cần nhớ: m và n là hai nghiệm đơn, và có thể mở rộng ra 3 hoặc 4 nghiệm đơn
VD: Tính tích phân sau: 
	1. 	2. 	3. 
Chú ý: Các bài sau ví dụ cho trường hợp mẫu số toàn là nghiệm đơn (3 nghiệm đơn). 
	3. 	4. 
Chú ý: Các bài sau ví dụ cho trường hợp mẫu số có nghiệm đơn và có nghiệm kép. 
5. 	6. 
7. 	8. 
VD: Tính các tích phân sau: 
	1. 	2. 
	3. 	4. 
TÍCH PHÂN HÀM LƯỢNG GIÁC
Dạng 1: .
Dạng 2: .
Phương pháp: 
Trường hợp 1: m là số lẻ, n chẵn.
Ta phân tích .
Ví dụ:.
Ta đặt t=cosx. 
Trường hợp 2: n là số lẻ, m số chẵn. 
Ta phân tích .
Ví dụ: .
Ta đặt t=sinx. 
Trường hợp 3: m và n cùng lẻ. 
Ta phân tích sinx hoặc cosx. 
Ta đặt t=cosx hoặc t=sinx. 
Trường hợp 4: m và n đều chẵn.
Ta dùng công thức hạ bậc. 
Đưa về hàm theo tanx hoặc cotx. Đổi biến với t=tanx hoặc t=cotx. 
Các công thức lượng giác thường áp dụng:
Các hằng đẳng thức lượng giác cơ bản :
 ( với ,k Î Z )
 ( với ,k Î Z )
 ( với ,k Î Z )
 ( với ,k Î Z )
 ( với ,k Î Z )
Công thức nhân đôi :
BÀI TẬP ÁP DỤNG
Bài 1: Tính các tích phân sau: 
	1. . 	2. 
	3. 	4. 
Bài 2: Tính các tích phân sau: 
	1. 	2. 
ADCT: 
	3. 	4. 
ADCT: 
Bài 3: Tính các tích phân sau: 
1. . 	2. 
	3. 	4. 
	5. 	6. 
	BÀI TẬP LUYỆN TẬP 
Bài 1: Tính các tích phân sau.
	1. I=	2. I=.
	3. I=	4. I=
Bài 2: Tính các tích phân sau.
	1. I=	2. I=.
	3. I=	4. I=
	5. I=	6. I=
	7. I=	8. I=
	9. I=	10. 
	11..	12.