Toán học khối 12 - Phương pháp tọa độ

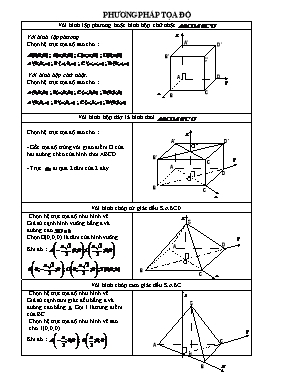
PHƯƠNG PHÁP TỌA ĐỘ
 Với hình lập phương hoặc hình hộp chữ nhật 
Với hình lập phương . 
Chọn hệ trục tọa độ sao cho : 
 Với hình hộp chữ nhật. 
Chọn hệ trục tọa độ sao cho : 
D’
A’
B’
C’
D
A
B
C
 Với hình hộp đáy là hình thoi 
Chọn hệ trục tọa độ sao cho : 
- Gốc tọa độ trùng với giao điểm O của hai đường chéo của hình thoi ABCD
- Trục đi qua 2 tâm của 2 đáy
A
B
C
D
D’
C
A’
B’
O
O’
Với hình chóp tứ giác đều S.ABCD
Chọn hệ trục tọa độ như hình vẽ 
Giả sử cạnh hình vuông bằng a và đường cao 
Chọn O(0;0;0) là tâm của hình vuông
Khi đó : 
S
O
A
D
C
B
Với hình chóp tam giác đều S.ABC
Chọn hệ trục tọa độ như hình vẽ 
Giả sử cạnh tam giác đều bằng a và đường cao bằng . Gọi I là trung điểm của BC
Chọn hệ trục tọa độ như hình vẽ sao cho I(0;0;0) 
Khi đó : 
I
H
C
B
A
S
Với hình chóp S.ABCD có ABCD là hình chữ nhật và SA (ABCD)
ABCD là hình chữ nhật 
chiều cao bằng 
Chọn hệ trục tọa độ như hình vẽ sao cho A(0;0;0) 
Khi đó : 
S
D
A
C
O
B
Với hình chóp S.ABC có ABCD là hình thoi và SA (ABCD)
ABCD là hình thoi cạnh 
chiều cao bằng 
Chọn hệ trục tọa độ như hình vẽ sao cho O(0;0;0) 
S
C
D
A
O
B
Với hình chóp S.ABC có SA (ABC) và ABC vuông tại A
Tam giác ABC vuông tại A có đường cao bằng . 
Chọn hệ trục tọa độ như hình vẽ sao cho A(0;0;0) 
 Khi đó : 
C
B
A
S
Với hình chóp S.ABC có SA (ABC) và ABC vuông tại B
Tam giác ABC vuông tại B có đường cao bằng . 
Chọn hệ trục tọa độ như hình vẽ sao cho B(0;0;0) 
 Khi đó : 
B
A
C
S
Với hình chóp S.ABC có (SAB) (ABC), SAB cân tại S
và ABC vuông tại C
 ABC vuông tại C 
chiều cao bằng 
H là trung điểm của AB
Chọn hệ trục tọa độ như hình vẽ sao cho C(0;0;0) 
Khi đó : 
S
H
C
B
A
Với hình chóp S.ABC có (SAB) (ABC), SAB cân tại S
và ABC vuông tại A
 ABC vuông tại A 
chiều cao bằng 
H là trung điểm của AB
Chọn hệ trục tọa độ như hình vẽ sao cho A(0;0;0) 
Khi đó : 
S
C
B
A
H
Với hình chóp S.ABC có (SAB) (ABC), SAB cân tại S
và ABC vuông cân tại C
 Tam giác ABC vuông cân tại C có 
 đường cao bằng . 
 H là trung điểm của AB
Chọn hệ trục tọa độ như hình vẽ sao cho H(0;0;0) 
 Khi đó : 
A
H
C
B
S
II. Bài tập áp dụng
Bài toán 1. Cho tứ diện OABC có các tam giác OAB,OBC,OCA đều là tam giác vuông tại đỉnh O. Gọi lần lượt là góc hợp bởi các mặt phẳng (OBC),(OCA),(OAB) với mặt phẳng (ABC).Chứng minh rằng : 
( SGK Hình 11, trang 96, Văn Như Cương chủ biên, NXBGD 2000, SGK Hình 12, trang 106, Văn Như Cương chủ biên, NXBGD 2000 ) 
 Hướng dẫn
 Bài giải
Dựng hình : 
Chọn hệ trục toạ độ Đêcac vuông góc như sau : ; ; ; 
O
C’
C
B
A
Tìm vectơ pháp tuyến của : 
Mặt phẳng (ABC) 
Mặt phẳng (OBC) 
Mặt phẳng (OCA) 
Mặt phẳng (OAB)
 vì : vì : vì : 
Sử dụng công thức tính góc giữa hai mặt phẳng: 
Kết luận
Bài toán 2. Bằng phương pháp toạ độ hãy giải bài toán sau :
Cho hình lập phương có cạnh bằng a.
a.Chứng minh rằng đường chéo vuông góc với mặt phẳng 
b.Chứng minh rằng giao điểm của đường chéo và mặt phẳng là trọng tâm của 
 tam giác .
c.Tìm khoảng cách giữa hai mặt phẳng và 
d.Tìm cosin của góc tạo bởi hai mặt phẳng và 
( SGK Hình 12, trang 112, Văn Như Cương chủ biên, NXBGD 2000 ) 
Hướng dẫn
Bài giải
Dựng hình : 
Chọn hệ trục toạ độ Đêcac vuông góc như sau : ; 
 ; 
 ; 
 ; 
C
G
–
C’
A’
B’
D’
D
B
A
a. Chứng minh : Nếu 
Ta có : 
Vì Nên 
b. Chứng minh : G là trọng tâm của tam giác Phương trình tham số của đường thẳng 
Phương trình tổng quát của mặt phẳng 
Trong đó vectơ pháp tuyến của mặt phẳng 
Gọi Toạ độ giao điểm G của đường thẳng và mặt phẳng là nghiệm của hệ : (1) 
 Mặt khác : (2) 
So sánh (1) và (2), kết luận 
Vậy giao điểm G của đường chéo và mặt phẳng là trọng tâm của tam giác 
c. Tính 
 Phương trình tổng quát của mặt phẳng Trong đó vectơ pháp tuyến của mặt phẳng 
Ta có : 
 // 
d. Tính 
Vec tơ pháp tuyến của là 
Vectơ pháp tuyến của : 
Vec tơ pháp tuyến củalà Vectơ pháp tuyến của : 
Bài toán 3. Cho hình lập phương có cạnh bằng a.
Chứng minh hai đường chéo và của hai mặt bên là hai đường thẳng chéo nhau. Tìm khoảng cách giữa hai đường thẳng chéo nhau và 
Hướng dẫn
Bài giải
Dựng hình : 
Chọn hệ trục toạ độ Đêcac vuông góc như sau : 
 ; ; ; 
 ; 
 ; 
D
B
C’
B’
A’
D’
C
A
Chứng minh và chéo nhau, ta chứng minh ba vectơ không đồng phẳng.
 Cần chứng minh 
tích hỗn hợp của ba vectơ khác 0
 Ta có : 
 ; 
 ba vectơ không đồng phẳng. 
hay và chéo nhau. 
Tính 
Bài toán 4. Trong không gian với hệ toạ độ cho hình chóp S.ABCD có đáy ABCD là hình thoi. AC cắt BD tại gốc toạ độ O. Biết ; ; . Gọi M là trung điểm của SC .
	1. Tính góc và khoảng cách giữa hai đường thẳng SA và BM
	2. Giả sử mặt phẳng (ABM) cắt đường thẳng SD tại N. 
 	 Tính thể tích khối chóp S.ABMN. 
 ( trích đề thi tuyển sinh ĐH&CĐ khối A năm 2004 )
Hướng dẫn
Bài giải
Dựng hình : 
Chọn hệ trục toạ độ Đêcac vuông góc như sau : ; ; ; 
Ta có : 
; ; ; 
B
 A
C
D
S
N
M
O
1a.Tính góc giữa SA và BM 
 Gọi là góc giữa SA và BM Sử dụng công thức tính góc giữa hai đường thẳng.
Ta có : 
1b. Tính khoảng cách giữa SA và BM
Chứng minh SA và BM chéo nhau Sử dụng công thức tính khoảng cách giữa hai đường thẳng chéo nhau
 ; 
 2. Tính thể tích khối chóp S.ABMN. 
 Dễ dàng nhận thấy : 
Trong đó : 
 N là trung điểm của SD Toạ độ trung điểm N ; ; 
Kết luận
Vậy (đvtt)
Bài toán 5 . Trong không gian với hệ toạ độ cho hình lăng trụ đứng với ; ; ; .
Tìm toạ độ các đỉnh ;. Viết phương trình mặt cầu có tâm là A và tiếp xúc với mặt phẳng . Gọi M là trung điểm của . Viết phương trình mặt phẳng (P) đi qua hai điểm A, M và song song với . ( trích đề thi tuyển sinh ĐH&CĐ khối B năm 2005 )
Hướng dẫn
Bài giải
Dựng hình : 
Chọn hệ trục toạ độ Đêcac vuông góc như sau :; 
Với : 
 ; ; ; 
 Toạ độ trung điểm M của 
A1	
 A	
B	
C	
C1	
O	
B1	
–	
M	
Toạ độ hai đỉnh ;.
Ta có : 
Phương trình mặt cầu có tâm là A và tiếp xúc với mặt phẳng 
 Viết phương trình mp 
 Tìm bán kính của mặt cầu (S) 
Vectơ pháp tuyến của mp 
 Phương trình tổng quát của mp :
 Bán kính của mặt cầu (S) : 
Phương trình mặt cầu (S) :
(S) 
 Phương trình mặt phẳng (P) : 
Tìm vectơ pháp tuyến của (P) ; 
Vectơ pháp tuyến của (P) : 
Phương trình mặt phẳng (P) : 
Bài toán 6 . Cho hình tứ diện ABCD có cạnh AD vuông góc với mặt phẳng(ABC); ; ; . Tính khoảng cách từ điểm A đến mặt phẳng (BCD) ( trích đề thi tuyển sinh ĐH&CĐ khối D năm 2002 )
Hướng dẫn
Bài giải
Dựng hình : 
 có : nên vuông tại A Chọn hệ trục toạ độ Đêcac vuông góc như sau ; ; ; 
Tính : 
I
H
D
C
B
A
Viết phương trình tổng quát của mặt phẳng (BCD)
 Phương trình tổng quát của mặt phẳng (BCD) 
Sử dụng công thức tính khoảng cách từ một điểm đến một mặt phẳng 
Bài toán 7 . Cho hai nửa đường thẳng và vuông góc với nhau và nhận là đoạn vuông góc chung. Lấy điểm M trên và điểm N trên sao cho . Xác định tâm I và tính theo bán kính R của mặt cầu ngoại tiếp tứ diện ABMN. Tính khoảng cách giữa hai đường thẳng AM và BI
Hướng dẫn
Bài giải
Dựng hình : 
Dựng 
Chọn hệ trục toạ độ Đêcac vuông góc như sau : ; ; 
Toạ độ trung điểm I của MN 
1a. Xác định tâm I của mặt cầu ngoại tiếp tứ diện ABMN 
Chú ý : 
B
N
A
I
M
Hai tam giác AMN và BMN là hai tam giác vuông nhận MN là cạnh huyền nên trung điểm của MN là tâm của mặt cầu ngoại tiếp tứ diện ABMN 
 1b.Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABMN
Ta có : 
 Bán kính mặt cầu : 
 2. Tính 
Chứng minh AM và BI chéo nhau 
Sử dụng công thức tính khoảng cách giữa hai đường thẳng chéo nhau
Ta có : ; ; 
Bài toán 8 . Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông cạnh . Gọi E là điểm đối xứng của D qua trung điểm của SA, M là trung điểm của AE, N là trung điểm của BC. Chứng minh MN vuông góc với BD và tính (theo ) khoảng cách giữa hai đường thẳng MN và AC. ( trích đề thi tuyển sinh ĐH&CĐ khối B năm 2007 )
Hướng dẫn
Bài giải
Dựng hình :
 Gọi O là tâm của hình vuông ABCD 
 Chọn hệ trục toạ độ Đêcac vuông góc như sau :
; S ; 
A ; C D ; B
N
A
P
M
E
O
C
S
D
B
Toạ độ trung điểm P của SA P; E
M N 
 Vì : 
Tính (theo a) khoảng cách giữa hai đường thẳng MN và AC. 
Chứng minh MN và AC chéo nhau 
 Sử dụng công thức tính khoảng cách giữa hai đường thẳng chéo nhau 
Ta có : 
 Vì : 
 MN và AC chéo nhau 
Bài toán 9 . Cho tứ diện ABCD, có AD vuông góc với mặt phẳng (ABC) và tam giác ABC vuông tại A; . 
Tính diện tích S của tam giác BCD theo 
Chứng minh rằng : 
Hướng dẫn
Bài giải
Chọn hệ trục tọa độ như hình vẽ sao cho A(0;0;0)
 Khi đó : 
Ta có : 
Áp dụng bất đẳng thức Côsi :
C
A
D
B
Tính diện tích S của tam giác BCD b. Chứng minh : 
Ta có : 
Bài toán 10 . Cho hình chóp tam giác đều S.ABC đỉnh S độ dài các cạnh đáy bằng . Gọi M, N lần lượt là trung điểm của các cạnh SB, SC. Tính theo diện tích tam giác AMN. Biết rằng mặt phẳng (AMN) vuông góc với mặt phẳng (SBC).
Hướng dẫn
Bài giải
Chọn hệ trục tọa độ như hình vẽ 
 Gọi I là trung điểm của BC
Chọn hệ trục tọa độ như hình vẽ sao cho I(0;0;0) 
Khi đó : 
N
M
I
H
A
C
B
S
+ Pháp vectơ của mp (AMN) :
+ Pháp vectơ của mp (SBC) : 
Diện tích tam giác AMN :
 đvdt
Bài toán 11 . Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh ; ; và mặt phẳng (SAB) vuông góc với mặt phẳng đáy. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC . Tính theo thể tích khối chóp S.BMDN và tính cosin của góc giữa hai đường thẳng SM, DN ( trích đề thi tuyển sinh ĐH &CĐ khối B năm 2008 )
Hướng dẫn
Bài giải
Dựng hình :
 Gọi H là hình chiếu vuông góc của S trên AB SH (ABCD) 
Ta có : 
vuông tại S 
Do đó : đều
 Chọn hệ trục toạ độ Đêcac vuông góc như sau :; S ; A ; B ; D ; M ; N
K
D
H
N
M
C
B
A
S
+ Thể tích khối chóp S.BMDN
 ; 
+ Công thức tính góc giữa SM, DN 
+ Tính cosin của góc giữa SM, DN 
Bài toán 12 . Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông, , cạnh bên . Gọi M là trung điểm của BC. Tính theo thể tích của khối lăng trụ ABC.A’B’C’ và khoảng cách giữa hai đường thẳng AM, B’C ( trích đề thi tuyển sinh ĐH &CĐ khối D năm 2008 )
Hướng dẫn
Bài giải
Dựng hình :
 Chọn hệ trục toạ độ Đêcac vuông góc như sau :
A ; C; B’ 
M 
 ; 
Chứng minh AM và B’C chéo nhau
A
C
C’
A’
B’
M
B
+ Thể tích của khối lăng trụ ABC.A’B’C’ 
 đvtt
+ Khoảng cách giữa AM và B’C
Vì : 
 AM và B’C chéo nhau
Bài toán 13 . Cho hình chóp S.ABCD có đáy ABCD là hình thang , , , SA vuông góc với đáy và . Gọi M,N lần lượt là trung điểm của SA và SD. Chứng minh rằng BCNM là hình chữ nhật và tính thể tích của khối chóp S.BCNM theo ( trích đề thi tuyển sinh Cao đẳng năm 2008 )
Hướng dẫn
Bài giải
Dựng hình :
 Chọn hệ trục toạ độ Đêcac vuông góc như sau :
 ; B ; C; D ; S
M ; N 
 ; 
 ; 
 ; 
S
N
M
D
A
B
C
+ Chứng minh BCNM là hình chữ nhật
 BCNM là hình chữ nhật
+ Tính thể tích của khối chóp S.BCNM theo 
 đvtt
Bài toán 14 . Cho hình chóp S.ABCD có đáy là hình vuông cạnh , . Mặt phẳng qua BC hợp với AC một góc 300 , cắt SA, SD lần lượt tại M, N. Tính diện tích thiết diện BCNM
Hướng dẫn
Bài giải
Dựng hình :
 Chọn hệ trục toạ độ Đêcac vuông góc như sau :
 ; B ; C; D ; S
Đặt 
 M 
Xác định vị trí điểm M
S
N
M
D
A
B
C
 ; 
Ta có : 
vuông cân tại A 
Pháp vectơ của mặt phẳng :
Vectơ chỉ phương của đường thẳng AC :
mặt phẳng hợp với AC một góc 300
 M là trung điểm của SA
+ BCNM là hình thang vuông
+ Diện tích thiết diện BCNM :
Bài toán 15 . Cho hình chóp O.ABC có đôi một vuông góc. Điểm M cố định thuộc tam giác ABC có khoảng cách lần lượt đến các mặt phẳng (OBC); (OCA); (OAB) lá 1; 2; 3. Tính để thể tích khối chóp O.ABC nhỏ nhất.
Hướng dẫn
Bài giải
Dựng hình :
 Chọn hệ trục toạ độ Đêcac vuông góc như sau : 
 A ; B; C 
 M 
A
B
C
C
M
O
H
B
E
A
+Thể tích khối chóp O.ABC
Giải hệ : 
+ Phương trình mặt phẳng (ABC) :
(ABC) : 
Áp dụng bất đẳng thức Côsi :
Bài toán 16 . Cho hình chóp tứ giác đều S.ABCD có các cạnh đều bằng . 
Tính thể tích khối chóp S.ABCD
Tính khoảng cách từ điểm A đến mặt phẳng (SCD)
Tính góc giữa SB và mặt phẳng (SCD)
Hướng dẫn
Bài giải
Dựng hình :
 Gọi 
 Chọn hệ trục toạ độ Đêcac vuông góc như sau :
; S ; 
A ; C D ; B
Phương trình mặt phẳng (SCD)
(SCD):
C
A
O
S
D
B
a.Tính thể tích khối chóp S.ABCD
Khoảng cách từ điểm A đến mặt phẳng (SCD)
Phương trình mặt phẳng (SCD)
(SCD):
Bài toán 17 . Cho hình chóp S.ABCD có đáy là hình thang , , , SA vuông góc với đáy và . Gọi H là hình chiếu của A trên SB. Chứng minh tam giác SCD vuông và tính theo khoảng cách từ H đến mặt phẳng (SCD) ( trích đề thi tuyển sinh ĐH &CĐ khối D năm 2007 )
Hướng dẫn
Bài giải
Dựng hình :
 Chọn hệ trục toạ độ Đêcac vuông góc như sau :
 ; B ; C; D ; S
+ Tìm tọa độ điểm H là hình chiếu vuông góc của A trên SB
Phương trình tham số của SB :
SB : ()
+ Viết phương trình mặt phẳng (SCD)
(SCD) đi qua điểm S và nhận vectơ làm pháp vectơ
(SCD) : 
S
H
A
I
D
B
C
+ Chứng minh tam giác SCD vuông
 ; 
Tam giác SCD vuông tại C
+ Tính ( theo ) khoảng cách từ H đến (SCD)
Tọa độ điểm H :
+ Khoảng cách từ H đến (SCD)
Phương trình mặt phẳng (SCD)
(SCD) : 
 z
 S
 y
 B O A
 M 
 C
 x 
Dựng hệ trục tọa độ như hình vẽ, gốc tọa độ tại M.