Toán học khối 12 - Chuyên đề Nguyên hàm, tích phân

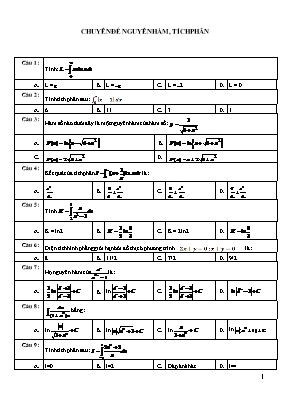
CHUYÊN ĐỀ NGUYÊN HÀM, TÍCH PHÂN
C©u 1 : 
Tính: 
A.
L = p
B.
L = -p
C.
L = -2
D.
L = 0
C©u 2 : 
Tính tích phân sau: 
A.
6
B.
11
C.
3
D.
1
C©u 3 : 
Hàm số nào dưới đây là một nguyên hàm của hàm số: 
A.
B.
C.
D.
C©u 4 : 
Kết quả của tích phân là:
A.
B.
C.
D.
C©u 5 : 
Tính 
A.
K = ln2
B.
C.
K = 2ln2
D.
C©u 6 : 
Diện tích hình phẳng giới hạn bởi đồ thị có phương trình là:
A.
8
B.
11/2
C.
7/2
D.
9/2
C©u 7 : 
Họ nguyên hàm củalà:
A.
B.
ln
C.
D.
C©u 8 : 
bằng:
A.
ln
B.
ln
C.
ln
D.
ln
C©u 9 : 
Tính tích phân sau: 
A.
I=0
B.
I=2
C.
Đáp án khác
D.
I=4
C©u 10 : 
Thể tích khối tròn xoay tạo thành khi quay quanh trục hoành hình phẳng giới hạn bởi các đường và y=x2 là
A.
(đvtt)
B.
(đvtt)
C.
(đvtt)
D.
(đvtt)
C©u 11 : 
Cho hàm số F(x) là một nguyên hàm của hàm số và thì
A.
B.
C.
D.
C©u 12 : 
Diện tích hình phẳng giới hạn bởi đồ thị các hàm số là:
A.
B.
C.
D.
C©u 13 : 
Hàm số nào là nguyên hàm của f(x) = :
A.
F(x) = ln(1 + sinx)
B.
F(x) = 
C.
F(x) = 2tan
D.
F(x) = 1 + cot
C©u 14 : 
Tìm nguyên hàm 
A.
B.
Đáp án khác
C.
D.
C©u 15 : 
Hàm số là nguyên hàm của hàm số f(x) nào
A.
B.
C.
D.
Đáp án khác
C©u 16 : 
Diện tích hình phẳng giới hạn bởi và y=3|x| là:
A.
B.
C.
D.
C©u 17 : 
Tính: 
A.
B.
C.
D.
C©u 18 : 
Kết quả của tích phân: 
A.
B.
C.
D.
2+
C©u 19 : 
Nguyên hàm của hàm số là:
A.
B.
C.
Đáp án khác
D.
C©u 20 : 
Biết :. Mệnh đề nào sau đây đúng?
A.
a là một số chẵn
B.
a là một số lẻ
C.
a là số nhỏ hơn 3
D.
a là số lớn hơn 5
C©u 21 : 
Giá trị của tích phân là
A.
B.
C.
D.
Không tồn tại
C©u 22 : 
Biết tích phân = thì giá trị của a là
A.
B.
12
C.
D.
6
C©u 23 : 
Biết. Giá trị của a là:
A.
3
B.
ln2
C.
D.
2
C©u 24 : 
Tìm nguyên hàm của hàm số f(x) biết 
A.
B.
C.
D.
C©u 25 : 
Tính 
A.
I = 
B.
I = 5
C.
I = 
D.
I = 
C©u 26 : 
Tính Diện tích hình phẳng giới hạn bởi đường cong
 và 
A.
B.
C.
D.
C©u 27 : 
Diện tích hình phẳng giới hạn bởi các đường: là:
A.
B.
C.
D.
C©u 28 : 
Tính tích phân sau: 
A.
B.
C.
D.
C©u 29 : 
Tính tích phân sau: 
A.
B.
C.
D.
C©u 30 : 
Tính: 
A.
I = -ln2
B.
C.
I = 1
D.
I = ln2
C©u 31 : 
Thể tích khối tròn xoay tạo thành khi cho đường x2+(y-1)2=1 quay quanh trục hoành là
A.
(đvtt)
B.
(đvtt)
C.
(đvtt)
D.
(đvtt)
C©u 32 : 
Tính
A.
B.
C.
D.
C©u 33 : 
Diện tích hình phẳng giới hạn bởi đồ thị các hàm số là:
A.
5/3
B.
3
C.
2
D.
7/3
C©u 34 : 
Một nguyên hàm của hàm số: y = cos5x.cosx là:
A.
F(x) = sin6x
B.
C.
F(x) = cos6x
D.
C©u 35 : 
Cho . Khi đó giá trị của m là:
A.
Kết quả khác
B.
m=0; m=4
C.
m=4
D.
m=2
C©u 36 : 
Tính 
A.
I = 
B.
C.
I = - 3ln2
D.
I = 2ln3
C©u 37 : 
Tính
A.
I = 2
B.
C.
ln2
D.
C©u 38 : 
Diện tích hình phẳng giới hạn bởi hai đường y = x, y = x + sin2x và hai đường thẳng x = 0, x = là:
A.
S = (đvdt)
B.
S = (đvdt)
C.
S = (đvdt)
D.
S = (đvdt)
C©u 39 : 
Gọi F(x) là nguyên hàm của hàm sốthỏa mãn F(3/2) =0. Khi đó F(3) bằng:
A.
ln2
B.
2ln2
C.
–ln2
D.
-2ln2
C©u 40 : 
Với t thuộc (-1;1) ta có. Khi đó giá trị t là:
A.
B.
0
C.
1/2
D.
1/3
C©u 41 : 
Cho hình phẳng D giới hạn bởi: gọi S là diện tích hình phẳng giới hạn bởi D. gọi V là thể tích vật tròn xoay khi D quay quanh ox. Chọn mệnh đề đúng.
A.
S=ln2, 
B.
S=ln2; 
C.
S=ln3; 
D.
S=ln3; 
C©u 42 : 
Kết quả của tích phân là:
A.
B.
C.
D.
C©u 43 : 
Gọi F(x) là nguyên hàm của hàm sốthỏa mãnF(2) =0. Khi đó phương trìnhF(x) = x có nghiệm là:
A.
x = 0
B.
x = -1
C.
D.
x = 1
C©u 44 : 
Tính 
A.
I = 
B.
I = 
C.
I = 
D.
I = 2
C©u 45 : 
Hàm số nào là nguyên hàm của f(x) = :
A.
F(x) = 
B.
F(x) = 
C.
F(x) = 
D.
C©u 46 : 
Thể tích của vật thể tròn xoay tạo bởi khi quay hình phẳng giới hạn bởi các đường y = x2 – 2x, y = 0, x = 0, x = 1 quanh trục hoành Ox có giá trị bằng?
A.
(đvtt)
B.
(đvtt)
C.
(đvtt)
D.
(đvtt)
C©u 47 : 
Tính tích phân ta được kết quả:
A.
B.
C.
D.
C©u 48 : 
Họ nguyên hàm của hàm số: y = sin3x.cosx là:
A.
B.
C.
-cos2x + C
D.
tg3x + C
C©u 49 : 
Tích phân . Giá trị của a là:
A.
2
B.
4
C.
3
D.
1
C©u 50 : 
Hàm sốcó nguyên hàm là:
A.
B.
C.
D.
C©u 51 : 
Biết tích phân =aln2 +b . Thì giá trị của a là:
A.
7
B.
3
C.
1
D.
2
C©u 52 : 
Diện tích hình phẳng giới hạn bởi, x + y = 0 là:
A.
Đápsốkhác
B.
5
C.
D.
C©u 53 : 
Tính: 
A.
K = 3ln2
B.
C.
D.
C©u 54 : 
Tính tích phân
A.
B.
C.
D.
C©u 55 : 
Các đường cong y = sinx, y=cosx với 0 ≤ x ≤ và trục Ox tạo thành một hình phẳng. Diện tích của hình phẳng là:
A.
B.
2
C.
Đáp số khác.
D.
C©u 56 : 
Cho . Tìm I?
A.
B.
C.
D.
C©u 57 : 
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=x2 và đường thẳng y= - x+2 là
A.
(đvdt)
B.
11 (đvdt)
C.
Một kết quả khác
D.
7 (đvdt)
C©u 58 : 
Cho 
Phát biểu nào sau đây sai?
A.
Đáp án khác
B.
C.
D.
C©u 59 : 
Cho hình phẳng giới hạn bởi các đường y = 2x – x2 và y = 0. Thì thể tích vật thể tròn xoay được sinh ra bởi hình phẳng đó khi nó quay quanh trục Ox có giá trị bằng?
A.
 (đvtt)
B.
(đvtt)
C.
(đvtt)
D.
 (đvtt)
C©u 60 : 
Tính tích phân sau: 
A.
B.
C.
D.
Cả 3 đáp án trên
C©u 61 : 
Tính diện tích hình phẳng giới hạn bởi và 
A.
5
B.
3
C.
7
D.
9
C©u 62 : 
Tìm nguyên hàm của hàm số f(x) biết 
A.
B.
C.
D.
Đáp án khác
C©u 63 : 
Với giá trị nào của m > 0 thì diện tích hình phẳng giới hạn bởi hai đường y = x2 và y = mx bằng đơn vị diện tích ?
A.
m = 2
B.
m = 1
C.
m = 4
D.
m = 3
C©u 64 : 
Họ nguyên hàm của tanx là:
A.
-ln
B.
C.
ln
D.
ln(cosx) + C
C©u 65 : 
nguyên hàm của hàm sốbằng:
A.
B.
C.
D.
C©u 66 : 
Tính:
A.
B.
C.
D.
C©u 67 : 
Tìm a sao cho 
A.
Đáp án khác
B.
a = - 3
C.
a = 3
D.
a = 5
C©u 68 : 
Cho hàm số F(x) là một nguyên hàm của hàm số f(x) = cos3x và = thì
A.
B.
C.
D.
C©u 69 : 
Họ nguyên hàm của f(x) = sin
A.
B.
C.
D.
C©u 70 : 
Gọi F1(x) là nguyên hàm của hàm sốthỏa mãnF1(0) =0 và F2(x) là nguyên hàm của hàm sốthỏa mãnF2(0)=0. 
Khi đóphương trìnhF1(x) = F2(x) có nghiệm là:
A.
B.
C.
D.
C©u 71 : 
Một nguyên hàm của là:
A.
B.
C.
D.
C©u 72 : 
Diện tích hình phẳng giới hạn bởi: là:
A.
-9
B.
9
C.
D.
C©u 73 : 
Tìm nguyên hàm của hàm số f(x) biết 
A.
B.
C.
D.
Đáp án khác
C©u 74 : 
Họ nguyên hàm củalà:
A.
ln
B.
ln
C.
-ln
D.
ln
C©u 75 : 
Tính ?
A.
2
B.
1
C.
D.
e
C©u 76 : 
Cho là hàm số chẵn và chọn mệnh đề đúng
A.
B.
C.
D.
C©u 77 : 
bằng:
A.
B.
C.
D.
C©u 78 : 
Thể tích khối tròn xoay khi quay quanh trục Ox hình phẳng giới hạn bởi các đường có giá trị bằng: trong đó a,b là hai số thực nào dưới đây?
A.
a=27; b=5
B.
a=24; b=6
C.
a=27; b=6
D.
a=24; b=5
C©u 79 : 
Diện tích hình phẳng giới hạn bởi hai đường cong và là?
A.
( đvdt)
B.
( đvdt)
C.
 ( đvdt)
D.
 ( đvdt)
C©u 80 : 
Tính 
A.
I = 
B.
I = + 1
C.
I = 
D.
I = 
C©u 81 : 
Hình phẳng D giới hạn bởi y = 2x2 và y = 2x + 4 khi quay D xung quanh trục hoành thì thể tích khối tròn xoay tạo thành là:
A.
V = (đvtt)
B.
V = 72 (đvtt)
C.
V = (đvtt)
D.
V = (đvtt)
C©u 82 : 
Nguyên hàm của hàm số là:
A.
B.
C.
D.
C©u 83 : 
Biết giá trị của là:
A.
B.
C.
D.
C©u 84 : 
Cho S là diện tích hình phẳng giới hạn bởi đồ thị hàm sốvà trục Ox. Số nguyên lớn nhất không vượt quá S là:
A.
27
B.
7
C.
6
D.
10
C©u 85 : 
Xác định a,b,c để hàm sốlà một nguyên hàm của hàm số
A.
B.
C.
D.
C©u 86 : 
Cho hàm số và tính 
A.
B.
C.
D.
C©u 87 : 
Tính: 
A.
B.
C.
D.
C©u 88 : 
Tính diện tích hình phẳng được giới hạn bởi đường cong
 và hai trục tọa độ.
A.
B.
C.
D.
C©u 89 : 
Họ nguyên hàm của f(x) = là:
A.
F(x) = 
B.
F(x) = ln
C.
F(x) = ln
D.
F(x) = ln
C©u 90 : 
Tìm nguyên hàm của hàm số f(x) biết 
A.
B.
Tanx-1+C
C.
D.
Đáp án khác
C©u 91 : 
Tìm a thỏa mãn: 
A.
a=ln2
B.
a=0
C.
a=ln3
D.
a=1
C©u 92 : 
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=x3 , trục hoành và các đường thẳng x= -1, x=3 là
A.
(đvdt)
B.
(đvdt)
C.
(đvdt)
D.
(đvdt)
C©u 93 : 
Giá trị của tích phân bằng?
A.
B.
Đáp án khác
C.
2
D.
C©u 94 : 
Tính diện tích hình phẳng giới hạn bởi và hai tiếp tuyến tại và 
A.
B.
C.
D.
C©u 95 : 
Tính tích phân
A.
ln2
B.
ln8
C.
1
D.
6
C©u 96 : 
Một nguyên hàm của f(x) = xelà:
A.
B.
C.
D.
C©u 97 : 
Một nguyên hàm của hàm số 
A.
B.
C.
D.
C©u 98 : 
Cho hàm số . Gọi F(x) là một nguyên hàm của f(x), biết rằng F(1) = 4 thì
A.
B.
C.
D.
C©u 99 : 
Tính.
Lời giải sau sai từ bước nào:
Bước 1: Đặt
Bước 2: Ta có
Bước 3: 
Bước 4: Vậy
A.
Bước 4
B.
Bước 1
C.
Bước 2
D.
Bước 3
C©u 100 : 
Tính diện tích hình phẳng giới hạn bởi cácđường
 và 
A.
B.
C.
D.
 ®¸p ¸n 
Câu
ĐA
1
B
2
D
3
B
4
D
5
B
6
D
7
A
8
A
9
C
10
C
11
C
12
D
13
B
14
D
15
C
16
C
17
B
18
D
19
D
20
A
21
D
22
A
23
D
24
C
25
A
26
D
27
B
28
D
29
D
30
B
31
C
32
B
33
D
34
B
35
C
36
A
37
B
38
A
39
C
40
C
41
B
42
D
43
C
44
A
45
B
46
A
47
D
48
B
49
D
50
B
51
A
52
C
53
B
54
C
55
C
56
D
57
C
58
D
59
A
60
D
61
D
62
C
63
A
64
A
65
C
66
B
67
A
68
C
69
A
70
C
71
A
72
B
73
C
74
A
75
D
76
B
77
B
78
A
79
A
80
A
81
A
82
A
83
B
84
C
85
B
86
D
87
B
88
D
89
B
90
C
91
B
92
C
93
A
94
D
95
C
96
B
97
A
98
A
99
C
100
D
CHUYÊN ĐỀ NGUYÊN HÀM, TÍCH PHÂN
C©u 1 : 
Giá trị của là
A.
2
B.
4
C.
5
D.
3
C©u 2 : 
Nguyên hàm của hàm số là
A.
F(x) = 
B.
F(x) = 
C.
F(x) = 
D.
F(x) = 
C©u 3 : 
Nguyên hàm của hàm số 
A.
B.
C.
D.
C©u 4 : 
Cho hình phẳng (S) giới hạn bởi Ox và. Thể tích của khối tròn xoay khi quay (S) quanh Oxlà
A.
B.
C.
D.
C©u 5 : 
Đổi biến x=2sint tích phântrở thành
A.
B.
C.
D.
C©u 6 : 
Cho là hàm số lẻ và liên tục trên. Khi đó giá trị tích phân là:
A.
1
B.
-2
C.
2
D.
0
C©u 7 : 
Họ các nguyên hàm của hàm số là:
A.
.
B.
.
C.
.
D.
.
C©u 8 : 
Diện tích hình phẳng giới hạn bởi đường cong y = x2 + 1, tiếp tuyến với đường này tại điểm M(2; 5) và trục Oy là:
A.
2
B.
C.
D.
C©u 9 : 
Cho là hàm số chẵn và liên tục trênthỏa mãn . Khi đó giá trị Tích phân là:
A.
2
B.
C.
D.
1
C©u 10 : 
Họ nguyên hàm của hàm số là
A.
B.
C.
D.
C©u 11 : 
Tính thể tích V của khối tròn xoay tạo thành khi ta cho miền phẳng D giới hạn bởi các đường , y = 0, x=0, x = 1 quay quanh trục ox . Ta có
A.
B.
C.
D.
C©u 12 : 
là
A.
B.
C.
D.
C©u 13 : 
Họ nguyên hàm F(x) của hàm số là
A.
B.
C.
D.
Đáp số khác
C©u 14 : 
Tính diện tích hình phẳng được giới hạn bởi
A.
B.
C.
D.
Tất cả đều sai.
C©u 15 : 
Nguyên hàm
A.
B.
C.
D.
C©u 16 : 
Cho với a,b là các số thực. Tìm nguyên hàm F(x) của f(x) biết 
A.
B.
C.
D.
C©u 17 : 
Nguyên hàm của hàm số thỏa mãn điều kiện là
A.
B.
C.
D.
4
C©u 18 : 
Tính diện tích hình phẳng được giới hạn bởi
A.
B.
C.
D.
C©u 19 : 
Diện tích hình phẳng giới hạn bởi hai đường cong y = x3 – x và 
y = x – x2 là :
A.
B.
C.
Đáp án khác
D.
C©u 20 : 
Tính tích phân 
A.
B.
C.
D.
C©u 21 : 
Nếu , với a < d < b thì bằng
A.
 -2
B.
8
C.
0
D.
3
C©u 22 : 
Họ nguyên hàm của hàm số là
A.
B.
C.
D.
C©u 23 : 
Diện tích hình phẳng giới hạn bởi các đồ thị hàm số là:
A.
27ln2+1
B.
27ln2-3
C.
27ln2
D.
C©u 24 : 
Diện tích hình phẳng giới hạn bởi các đường (P): y =x2-2x+2 và các tiếp tuyến với (P) biết tiếp tuyến đi qua A(2;-2) là:
A.
B.
C.
D.
C©u 25 : 
Thể tíchvật thể tròn xoay khi quay hình phẳng giới hạn bởi các đườngquanh trục ox là:
A.
B.
C.
D.
C©u 26 : 
Nguyên hàm
A.
B.
C.
D.
C©u 27 : 
Tích phân bằng
A.
B.
4
C.
2
D.
3
C©u 28 : 
Nguyên hàm của hàm số trênlà 
A.
B.
C.
D.
C©u 29 : 
Tích phân
A.
B.
C.
D.
C©u 30 : 
Tính A = , ta có
A.
B.
C.
D.
Đáp án khác
C©u 31 : 
Tích phân
A.
B.
C.
D.
C©u 32 : 
Diện tích hình phẳng được giới hạn bởi hai đườngvàbằng (đvdt)
A.
B.
C.
D.
2
C©u 33 : 
Diện tích hình phẳng giới hạn bởi hai parabol là giá trị nào sau đây ?
A.
12 (đvdt)
B.
27 (đvdt)
C.
9 (đvdt)
D.
4 (đvdt)
C©u 34 : 
Nguyên hàm của hàm số là
A.
B.
C.
D.
C©u 35 : 
Cho . Khi đó, Giá trị của a là:
A.
B.
C.
D.
C©u 36 : 
Cho hình phẳng (S) giới hạn bởi Ox, Oy, y = 3x + 2. Thể tích của khối tròn xoay khi quay (S) quanh Oy là:
A.
B.
C.
D.
C©u 37 : 
Cho hai tích phân và , hãy chỉ ra khẳng định đúng:
A.
B.
Không so sánh được
C.
D.
C©u 38 : 
Kết quả của là:
A.
B.
C.
Đáp án khác
D.
C©u 39 : 
Hàm số có nguyên hàm trên K nếu
A.
xác định trên K
B.
có giá trị lớn nhất trên K
C.
liên tục trên K
D.
có giá trị nhỏ nhất trên K
C©u 40 : 
Hàm số nào sau đây không là nguyên hàm của hàm số 
A.
B.
C.
D.
C©u 41 : 
Họ nguyên hàm F(x) của hàm số là
A.
B.
C.
D.
C©u 42 : 
Diện tích hình phẳng nằm trong góc phần tư thứ nhất, giới hạn bởi đường thẳngvà đồ thị hàm số là
A.
5
B.
4
C.
3
D.
C©u 43 : 
Cho hình phẳng giới hạn bởi các đường. Thể tích của khối tròn xoay sinh bởi hình phẳng trên khi quay quanh trục hoành là
A.
B.
C.
D.
C©u 44 : 
Nguyên hàm của hàm số là:
A.
B.
C.
Đáp án khác
D.
C©u 45 : 
Tính diện tích hình phẳng được giới hạn bởi
A.
B.
C.
D.
C©u 46 : 
Tích phân
A.
B.
C.
D.
C©u 47 : 
Tính
A.
B.
C.
D.
C©u 48 : 
Họ nguyên hàm của hàm số là
A.
B.
C.
D.
C©u 49 : 
Diện tích hình phẳng giới hạn bởi các đồ thị hàm số vàlà:
A.
B.
C.
D.
2
C©u 50 : 
Họ nguyên hàm F(x) của hàm số là
A.
B.
C.
D.
C©u 51 : 
Diện tích hình phẳng giới hạn bởi các đường (P): y=2-x2 , (C): y=và Ox là:
A.
B.
C.
D.
C©u 52 : 
Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi đồ thị hàm số quanh trục ox là
A.
B.
C.
D.
C©u 53 : 
Tích phân bằng
A.
B.
C.
D.
C©u 54 : 
Thể tích của khối tròn xoay tạo lên bởi lên hình phẳng (H) giới hạn bởi các đường ; và trục Ox khí quay xung quanh Ox là
A.
B.
C.
D.
C©u 55 : 
Diện tích hình phẳng giới hạn bởi đồ thị hàm số và các tiếp tuyến với đồ thị hàm số biết tiếp tuyến đi qua M(5/2;6) có kết quả dạng khi đó a-b bằng
A.
B.
14
C.
5
D.
-5
C©u 56 : 
Biết F(x) là nguyên hàm của hàm số và F(2)=1. Khi đó F(3) bằng bao nhiêu:
A.
B.
C.
D.
C©u 57 : 
Thể tíchvật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường quanh trục ox có kết quả dạng khi đó a+b có kết quả là:
A.
11
B.
25
C.
17
D.
31
C©u 58 : 
Tính diện tích S của hình phẳng được giới hạn bởi các đườngvà , ta có
A.
B.
C.
D.
Đápsố khác
C©u 59 : 
Cặp hàm số nào sau đây có tính chất: Có một hàm số là nguyên hàm của hàm số còn lại?
A.
và	
B.
và
C.
và
D.
và	
C©u 60 : 
Vận tốc của một vật chuyển động là. Quãng đường vật đó đi được từ giây thứ 4 đến giây thứ 10 là :
A.
1200m
B.
36m
C.
1014m
D.
252m
C©u 61 : 
Thể tích khối tròn xoay tạo nên khi quay quanh trục Ox hình phẳng giới hạn bởi các đường y =(1- x)2, y = 0, x = 0 và x = 2 bằng:
A.
B.
C.
D.
C©u 62 : 
Hình phẳng giới hạn bởicó diện tích là:
A.
1
B.
C.
D.
C©u 63 : 
Thể tíchvật thể tròn xoay khi quay hình phẳng giới hạn bởi các đồ thị hàm số và x=2 quanh trục ox là:
A.
B.
C.
D.
C©u 64 : 
Thể tích khối tròn xoay được tạo bởi phép quay quanh trục Ox hình phẳng giới hạn bởi các đường y = x2 và x = y2 bằng:
A.
B.
C.
D.
C©u 65 : 
Họ nguyên hàm F(x) của hàm số là:
A.
B.
C.
D.
Đáp số khác
C©u 66 : 
Nguyên hàm
A.
B.
C.
D.
C©u 67 : 
Cho liên tục trên [0; 10] thỏa mãn : Khi đó, Giá trị của P = có giá trị là:
A.
1
B.
3
C.
2
D.
4
C©u 68 : 
Diện tích hình phẳng giới hạn bởiđồ thị hàm số và hai tiếp tuyến với đồ thị hàm số tai A(1;2) và B(4;5) có kết quả dạng khi đó: a+b bằng
A.
12
B.
C.
13
D.
C©u 69 : 
Diện tích hình phẳng giới hạn bởi đường cong, hai trục tọa độ và đường thẳng là:
A.
 (đvdt)
B.
 (đvdt)
C.
 (đvdt)
D.
4 (đvdt)
C©u 70 : 
Tính ta được kếtquả là :
A.
B.
C.
D.
C©u 71 : 
Cho . Tìm m để nguyên hàm F(x) của f(x) thỏa mãn F(0) = 1 và 
A.
B.
C.
D.
C©u 72 : 
Cho hàm số thỏa mãnvà f(-1)=1 thì f(2) bằng bao nhiêu:
A.
B.
C.
D.
C©u 73 : 
Để tìm nguyên hàm củathì nên:
A.
Dùng phương pháp đổi biến số, đặt 
B.
Dùng phương pháp lấy nguyên hàm từng phần, đặt
C.
Dùng phương pháp đổi biến số, đặt 
D.
Dùng phương pháp lấy nguyên hàm từng phần, đặt
C©u 74 : 
Diện tích hình phẳng giới hạn bởi đồ thị hàm số và đường thẳng y=3 là 
A.
B.
C.
D.
C©u 75 : 
Nguyên hàm của hàm số thỏa mãn điều kiện là
A.
B.
C.
D.
C©u 76 : 
Diện tích hình phẳng giới hạn bởi hai đường thẳng x = 0, và đồ thị của hai hàm số y = cosx, y = sinx là:
A.
B.
C.
2
D.
C©u 77 : 
Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường quanh trục ox là:
A.
B.
C.
D.
C©u 78 : 
Họ nguyên hàm F(x) của hàm số 
A.
B.
C.
D.
C©u 79 : 
Tính thể tích khối tròn xoay tạo bởi quay quanh trục Ox và hình phẳng giới hạn bởi
A.
B.
C.
D.
C©u 80 : 
Tính tích phân 
A.
B.
C.
D.
C©u 81 : 
Tìm hàm số F(x) biết rằng F’(x) = 4x3 – 3x2 + 2 và F(-1) = 3 
A.
F(x) = x4 – x3 - 2x + 3
B.
F(x) = x4 – x3 + 2x + 3
C.
F(x) = x4 – x3 - 2x -3
D.
F(x) = x4 + x3 + 2x + 3
C©u 82 : 
Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đườngquanh trục ox là:
A.
B.
C.
D.
C©u 83 : 
Họ các nguyên hàm của hàm số là:
A.
.
B.
C.
D.
C©u 84 : 
Thể tích vật thể tròn xoay sinh ra khi hình phẳng giới hạn bới các đường, , quay quanh trục Oy, có giá trị là kết quả nào sau đây ?
A.
 (đvtt)
B.
 (đvtt)
C.
 (đvtt)	
D.
 (đvtt)
C©u 85 : 
Tính ta được kết quả nào sau đây?
A.
Một kết quả khác
B.
C.
D.
C©u 86 : 
Kết quả của là:
A.
B.
C.
D.
C©u 87 : 
Diện tích hình phẳng giới hạn bởi đồ thị hàm số có kết quả dạng khi đó a-b bằng
A.
-3
B.
2
C.
3
D.
59
C©u 88 : 
Diện tích hình phẳng giới hạn bởi các đồ thị hàm số có kết quả là	
A.
B.
C.
D.
C©u 89 : 
Cho hình phẳng (S) giới hạn bởi Ox, Oy, y = cosxvà. Diện tích hình phẳng (S)là:
A.
B.
C.
D.
C©u 90 : 
Diện tích hình phẳng giới hạn bởi các đồ thị: vàcó kết quả là:
A.
B.
6
C.
D.
12
C©u 91 : 
Diện tích hình phẳng giới hạn bởi đồ thị hàm số và trục ox và đường thẳng x=1 là:
A.
B.
C.
D.
C©u 92 : 
Giá trị của là
A.
B.
C.
D.
C©u 93 : 
Tínhdiện tích S của hình phẳng được giới hạn bởi các đườngvà y = 0, ta có
A.
B.
C.
D.
C©u 94 : 
Diện tích hình phẳng giới hạn bởi (C): y= -x2+3x-2, d1:y = x-1 và d2:y=-x+2 có kết quả là	
A.
B.
C.
D.
C©u 95 : 
Diện tích hình phẳng giới hạn bởi các đồ thị: và y=x+3 có kết quả là:
A.
B.
C.
D.
C©u 96 : 
Tính 
A.
B.
C.
3
D.
C©u 97 : 
Họ nguyên hàm F(x) của hàm số là
A.
Cả (A), (B) và (C) đều đúng
B.
C.
D.
C©u 98 : 
Tích phân bằng
A.
1
B.
3
C.
2
D.
4
C©u 99 : 
Giả sử . Giá trị của là
A.
9
B.
3
C.
81
D.
8
C©u 100 : 
Diện tích hình phẳng giới hạn bởi đồ thị hàm số trục hoành và hai đường thẳng x=-2 , x=-4 là
A.
B.
C.
D.
12
 ®¸p ¸n M· ®Ò : 02
Câu
Đáp án
1
B
2
B
3
B
4
D
5
A
6
D
7
D
8
D
9
D
10
B
11
A
12
B
13
A
14
A
15
A
16
B
17
B
18
A
19
D
20
B
21
D
22
B
23
C
24
D
25
C
26
A
27
A
28
C
29
A
30
A
31
A
32
A
33
C
34
A
35
D
36
D
37
D
38
D
39
C
40
D
41
A
42
B
43
B
44
B
45
A
46
A
47
B
48
B
49
C
50
A
51
C
52
D
53
B
54
B
55
C
56
B
57
D
58
A
59
C
60
C
61
D
62
D
63
C
64
D
65
A
66
A
67
D
68
C
69
C
70
C
71
B
72
B
73
C
74
C
75
B
76
D
77
D
78
A
79
A
80
B
81
B
82
C
83
D
84
C
85
C
86
D
87
C
88
D
89
D
90
C
91
C
92
B
93
A
94
C
95
C
96
B
97
A
98
A
99
B
100
C
NGÂN HÀNG ĐỀ TRẮC NGHIỆM CHUYÊN ĐỀ NGUYÊN HÀM, TÍCH PHÂN
(MÃ ĐỀ 03)
C©u 1 : 
Nguyên hàm của hàm số bằng::
A.
B.
C.
 .
D.
C©u 2 : 
Diện tích hình phẳng giới hạn bởi và