Toán học - Đồ thị của hàm số

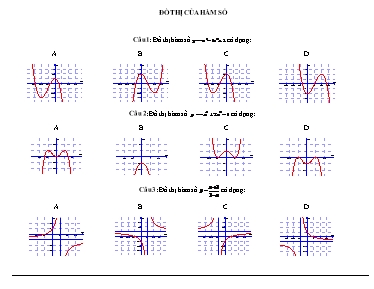
 ĐỒ THỊ CỦA HÀM SỐ
Câu 1: Đồ thị hàm số có dạng:
A
B
C
D
Câu 2: Đồ thị hàm số có dạng:
A
B
C
D
Câu 3: Đồ thị hàm số có dạng:
A
B
C
D
Câu 4: Đồ thị hàm số có dạng:
A
B
C
D
Câu 5: Đồ thị hàm số có dạng:
A
B
C
D
Câu 6: Đồ thị hàm số có dạng:
A
B
C
D
Câu 7: Đồ thị hình bên là của hàm số:
A. B. 
C. D. 
Câu 8: Đồ thị hình bên là của hàm số:
A. B. 
C. D. 
Câu 9: Đồ thị hình bên là của hàm số:
A. B. 
C. D. 
Câu 10: Đồ thị hình bên là của hàm số:
A. B. 
C. D. 
DẠNG ĐỒ THỊ CỦA 3 HÀM: BẬC BA, TRÙNG PHƯƠNG, NHẤT BIẾN
Hàm trùng phương có đồ thị đối xứng qua Oy
O
y
O
a > 0
a < 0
Hàm bậc ba: y = ax3+ bx2+cx+d	O
 Hàm trùng phương: y = ax4 + bx2 + c	 Hàm nhất biến
ĐƯỜNG TIỆM CẬN CỦA HÀM LŨY THỪA
HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
Hàm nhất biến có tâm đối xứng là giao điểm 2 đường tiệm cận
y’ > 0
a > 0
O
O
y
y
a, b cùng dấu (có 1 cực trị)
y’ = 0 vô nghiệm hoặc nghiệm kép ( k0 có cực trị)
y’ < 0
a > 0
a, b trái dấu (có 3 cực trị)
a > 0
a < 0
O
O
y
y
a > 0
a < 0
y’ = 0 có 2 nghiệm phân biệt (có 2 cực trị)
a < 0
a < 0
 Hàm bậc ba luôn có 1 tâm đối xứng là điểm uốn 	
● Hàm lũy thừa : Chỉ có 2 tiệm cận khi 
TCĐ: (Trục Oy) ; TCN (Trục Ox)
● Hàm số mũ ()
Dấu hiệu tiệm cận: Vì TCN 
● Hàm số logarit ()
Dấu hiệu tiệm cận: Vì điều kiện TCĐ 
ĐƯỜNG TIỆM CẬN CỦA HÀM PHÂN THỨC 	
Dấu hiệu TCĐ: Ptcó bao nhiêu nghiệm là có bấy nhiêu TCĐ
Nếu bậc của bậc của thì TCN 
Áp dụng Đ.N tìm TCĐ: Tồn tại 1 trong 4 TCĐ 	 
Nếu bậc của bậc của thì TCN 
Dấu hiệu TCN: 
Áp dụng Đ.N tìm TCN:Tồn tại hoặc TCN