Toán học - Chuyên đề 1: Hàm số

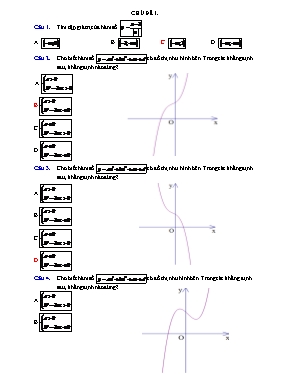
CHỦ ĐỀ 1. 
Tìm tập giá trị của hàm số .
A. .	B. .	C. .	D. .
Cho biết hàm số có đồ thị như hình bên. Trong các khẳng định sau, khẳng định nào đúng?
 A.. 	
B. .	
C..	
D. .
Cho biết hàm số có đồ thị như hình bên. Trong các khẳng định sau, khẳng định nào đúng?
A.. 	
B. .	
C..	
D. .
Cho biết hàm số có đồ thị như hình bên. Trong các khẳng định sau, khẳng định nào đúng?
A..	
B. .	
C. .	
D. .
Cho biết hàm số có đồ thị như hình bên. Trong các khẳng định sau, khẳng định nào đúng?
A.. 	B. .	
C. .D. .
Xác định dấu của nếu đồ thị hàm số có dạng như hình bên.
A. 	
B. . 
C. .	
D. .
Tìm để hàm số có đồ thị như hình bên
A. .
B. .
C. .
D. .
Tìm để đường thẳng cắt đồ thị hàm số tại hai điểm phân biệt.
A. .
B. .
C. .
D. .
Tìm tất cả các giá trị của tham số để hàm số có hai điểm cực trị.
A. . 	B. .	C. .	D. .
Tìm giá trị của tham số để đồ thị hàm số có một điểm cực trị duy nhất.
A. .	B. .	
C. .	D. Không có như thế.
 Tìm các bộ ba số để hàm số đồng biến trên hai khoảng ; nghịch biến trên khoảng và có đồ thị đi qua điểm .
A. .	B. .
C..	D. .
Cho hàm số . Trong các khẳng định sau, khẳng định nào đúng?
A. Hàm số đồng biến trên mỗi khoảng và.
B. Hàm số nghịch biến trên mỗi khoảng và.
C. Hàm số nghịch biến trên tập .
D. Hàm số nghịch biến với mọi .
Cho hai đường tròn có phương trình , . Tìm các bộ ba hằng số để đồ thị hàm số đi qua các tâm của mỗi đường tiệm cận của đồ thị tiếp xúc với .
A. .	B. .
C. .	D. .
Tìm các giá trị của tham số để hàm số có giá trị cực đại và giá trị cực tiểu trái dấu.
A. .	B. . 	C. .	D. .
Xét hàm số . Trong các khẳng định sau, khẳng định nào sai?
A. , .
B. Gốc tọa độ là tâm đối xứng của đồ thị hàm số.
C. Đồ thị hàm số cắt trục hoành tại hai điểm.
D. Đồ thị hàm số cắt trục tung tại điểm có tung độ .
Tìm các giá trị của tham số để phương trình . Có nghiệm duy nhất.
A. . 	B. .	C. . 	D. .
Tìm để đồ thị hàm số có là điểm cực đại và là một điểm cực tiểu.
A. . 	B..
C. . 	D..
Tìm tập hợp các điểm cực trị của hàm số .
A. . 	B. .	C. .	 D..
Tìm các tiệm cận ngang của đồ thị hàm số .
A.. 	B. . 	C. . 	D. và .
Đồ thị hàm số có bao nhiêu tiệm cận đứng?
A. . 	B. .	C. . 	D. .
Tìm tập hợp các giá trị của tham số để đồ thị hàm số có hai đường tiệm cận đứng phân biệt.
A. . 	B. .	C.. 	D..
Tìm tất cả các giá trị của tham số để hàm số có hai điểm cực trị nằm trong khoảng 
A. .	B. .	
C. .	D. . 
Tìm các giá trị của để đồ thị hàm số cắt trục hoành tại đúng hai điểm.
A. .	B. . 	C. .	D. .
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn .
A. . 	B. . 	C. . 	D. .
Tìm tất cả các giá trị của tham số để hàm số nghịch biến trên khoảng .
A. . 	B.. 	C. . 	D. .
Xét hàm số . Trong các khẳng định sau, khẳng định nào đúng?
A. Hàm số luôn đồng biến .
B. Hàm số không có cực trị.
C.Hàm số có hai cực trị.
D. Đồ thị hàm số có tiệm cận ngang.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số .
A. . 	B. .	 C. . 	D. .
Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số .
A. . 	B. .	 C. . 	D. .
Cho hàm số . Trong các khẳng định sau, khẳng định nào sai?
A. Đạo hàm của hàm số triệt tiêu và đổi dấu tại và tại .
B. Hàm số đạt cực trị tại và tại .
C. Hàm số đạt cực đại và đạt cực tiểu .
D. Đồ thị hàm số có hai điểm cực trị .
Hàm số đạt giá trị lớn nhất tại . Tìm .
A. .	B. . 	C. .	D. .
Tìm các giá trị của tham số để . 
A. . 	B. . 	C.. 	D. .
Tìm các giá trị của tham số để đường thẳng cắt đồ thị hàm số tại bốn điểm phân biệt.
A. . 	B. . 	C. . 	D. .
Kí hiệu là giá trị lớn nhất và giá trị nhỏ nhất của hàm số . Tính .
A. . 	B. . 	C. . 	D. .
Tìm các giá trị của tham số để đồ thị hàm số cắt đường thẳng tại ba điểm phân biệt sao cho gốc tọa độ và là ba đỉnh của một tam giác có diện tích bằng 2.
A. .	B. .	C. . 	D. .
Hàm số nào trong các hàm số cho dưới đây có thể có đồ thị như trong hình bên?
A. . 	B. . 	
C. 	D. .
Tìm tất cả các giá trị của tham số để hàm số nghịch biến trên khoảng .
A. . 	B. .	C. .	D. .
Hàm số đồng biến trên khoảng nào trong các khoảng cho sao đây?
A. .	B. .	C. .	D. .
Trong các hàm số sau, hàm số nào nghịch biến trên khoảng ?
A. . 	B. . 	C. .	D. .
Trong các hàm số sau đây, hàm số nào có cực trị?
A. .	B. .
C. .	D. .
Tìm các giá trị của để đường thẳng cắt đồ thị hàm số tại sáu điểm phân biệt.
A. .	B. . 	C. .	D. .
Tìm tất cả các giá trị của để đồ thị hàm số cắt trục hoành tại ba điểm phân biệt có hoành độ thỏa mãn điều kiện .
A. . 	B. . 	
C. 	.	D. .
Tìm tất cả các giá trị để hàm số nghịch biến trên khoảng .
A. .	B. . C. . D. .
Với các giá trị nào của , đồ thị hàm số có hai điểm cực trị cách đều gốc tọa độ?
A. .	 B. . C. . D. .