Toán học - Các công thức nguyên hàm mở rộng

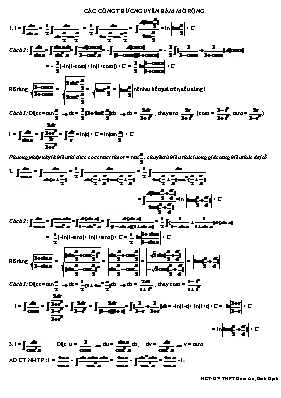
CÁC CÔNG THỨC NGUYÊN HÀM MỞ RỘNG
1. I = = = = = ln + C
Cách 2: === -= - 
 = - (-ln|1-cosx| + ln|1+cosx|) + C = + C
Rõ ràng = = = nên hai kết quả trên, đều đúng!. 
Cách 3: Đặt t = tan dt = dx dx = ; thay sinx (cosx = ; tanx =)
I = = = = ln|t| + C = ln|tan| + C
Phương pháp này là biểu thị sinx, cosx, tanx theo t = tan, chuyển từ biểu thức lượng giác sang biểu thức đại số 
2. = = = 
 ==ln + C
Cách 2: === = 
 = (-ln|1-sinx| + ln|1+sinx|) + C = + C 
Rõ ràng = = = = 
Cách 3: Đặt t = tan dt = dx dx = ; thay cosx = 
 I = = = = = = -ln|1-t| + ln|1+t| + C = + C
 = ln + C
3. I = Đặt u = du = dx; dv = v = tanx
AD CT NH TP : I = - = - = - I1
Với I1 = = = -= I - 
Từ đó I = - I1 = - (I - ln) 
 2I = + ln + C I = ( + ln) + C
4. Đặt 
 Tính 
5. === + C
6. I = Đặt x = atant dx = ; === 
=== ln + C , với t = arctan.
Cách 2: Đặt t = x+ dt = (1+)dx = dx = dx dx = dt
Từ đó I = == = ln|t| + C = + C
7. I = Đặt x = dx = ; = = a.tant
= = = ln + C, với t = arccos.
Cách 2: Đặt t = x + dt = (1+)dx = dx = dx 
 dx = dt Từ đó I = == = ln|t| + C = + C
8. = = ln|x2 + a| + C 9. = = ln|x2 - a| + C
10. === + C = + C
11. === + C = + C
12. Đặt x = atant dx = ; === 
 = = a2 = a2.( + ln) + C, với t = arctan.
Cách 2: I = = = + = I1 + I2
Với I1 = = a2 (chọn C = 0)
I2 = = Đặt u = x du = dx; dv = dx v = 
ADCT NHTP I2 = x- = = x- I
I = I1 + I2 = a2 + x- I I = ( x+ a2) + C
13. I = =( x- a2 ) + C 
Đặt x = dx = ; = = a.tant
I = = = a2 = a2= a2( - )
Với =( + ln) + C; = ln + C
Cách 2: I = = = - = I2 - I1
Với I1 = = a2. (chọn C = 0)
I2 = = Đặt u = x du = dx; dv = dx v = 
ADCT NHTP I2 = x- = = x- I
I = I2 - I1 = x- I - a2 I = ( x- a2) + C
Good luck