Tập các bài toán về đường tròn trong các đề thi

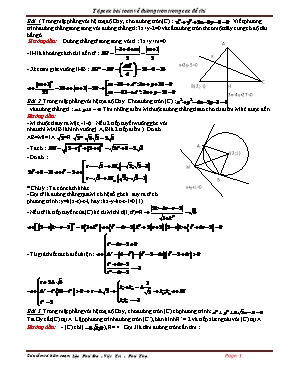
Bài 1 Trong mặt phẳng với hệ toạ độ Oxy, cho đường tròn (C) : . Viết phương trình đường thẳng song song với đường thẳng d: 3x+y-2=0 và cắt đường tròn theo một dây cung có độ dài bằng 6.
B(2;-1)
A
C
x+2y-5=0
3x-4y+27=0
H
K
 Hướng dẫn: Đường thẳng d' song song với d : 3x+y+m=0 
- IH là khoảng cách từ I đến d' : 
- Xét tam giác vuông IHB : 
Bài 2 Trong mặt phẳng với hệ tọa độ Oxy. Cho đường tròn (C) :
 và đường thẳng d : . Tìm những điểm M thuộc đường thẳng d sao cho từ điểm M kẻ được đến Hướng dẫn: 
M
x+y+1=0
A
B
I(2;1)
- M thuộc d suy ra M(t;-1-t). . Nếu 2 tiếp tuyến vuông góc với 
nhau thì MAIB là hình vuông ( A,B là 2 tiếp điểm ). Do đó AB=MI= IA=R=.
- Ta có : 
- Do đó : .
* Chú ý : Ta còn cách khác 
- Gọi d' là đường thẳng qua M có hệ số góc k suy ra d' có phương trình : y=k(x-t)-t-1, hay : kx-y-kt-t-1=0 (1) .
- Nếu d' là tiếp tuyến của (C) kẻ từ M thì d(I;d')=R 
- Từ giả thiết ta có điều kiện : 
-
Bài 3 Trong mặt phẳng với hệ toạ độ Oxy, cho đường tròn (C) có phương trình: Tia Oy cắt (C) tại A. Lập phương trình đường tròn (C’), bán kính R’ = 2 và tiếp xúc ngoài với (C) tại A
Hướng dẫn: - (C) có I(), R= 4 . Gọi J là tâm đường tròn cần tìm :
I(-2;0)
A(0;2)
y
x
 J(a;b) 
-Do (C) và (') tiếp xúc ngoài với nhau cho nên khoảng cách IJ =R+R'
- Vì A(0;2) là tiếp điểm cho nên : 
- Do đó ta có hệ : 
- Giải hệ tìm được : b=3 và a= . 
* Chú ý : Ta có cách giải khác .
- Gọi H là hình chiếu vuông góc của J trên Ox suy ra OH bằng a và JH bằng b 
- Xét các tam giác đồng dạng : IOA và IHJ suy ra : 
- Từ tỷ số trên ta tìm được : b=3 và a= .
Bài 4. Trongmặtphẳngtoạđộ Oxy chođườngtròn (C) : x2 + y2 + 4x – 6y + 9 = 0 vàđiểm M( 1; - 8).Viếtphươngtrìnhđườngthẳng d qua M saocho d cắt (C) tạihaiđiểm A,B phânbiệtmàdiệntích tam giác ABI đạtgiátrịlớnnhất.
Hướng dẫn:
Bài 5. Với I làtâmcủađườngtròn (C).Cho A(1 ; 4) vàhaiđườngthẳng b : x + y – 3 = 0 ; c : x + y – 9 = 0. Tìmđiểm B trênb ,điểm C trên c saocho tam giác ABC vuôngcântại A.
Hướng dẫn:
Bài 6 
Bài 7 
Bài 8 Trong mặt phẳng với hệ tọa độ Oxy cho đường tròn hai đường tròn cùng đi qua M(1; 0). Viết phương trình đường thẳng qua M cắt hai đường tròn lần lượt tại A, B sao cho MA= 2MB
Hướng dẫn: * Cách 1. 
- Gọi d là đường thẳng qua M có véc tơ chỉ phương 
- Đường tròn , suy ra :
- Nếu d cắt tại A : 
- Nếu d cắt tại B : 
- Theo giả thiết : MA=2MB 
- Ta có : 
* Cách 2.
- Sử dụng phép vị tự tâm I tỉ số vị tự k=. ( Học sinh tự làm )
Bài 9 Trong hệ tọa độ Oxy, cho hai đường tròn có phương trình và Lập phương trình tiếp tuyến chung của và 
Hướng dẫn: : - Ta có :
- Nhận xét : không cắt 
- Gọi d : ax+by+c =0 ( ) là tiếp tuyến chung , thế thì :
. Mặt khác từ (1) : 
- Trường hợp : a=2b thay vào (1) :
- Do đó ta có hai đường thẳng cần tìm :
- Trường hợp : , thay vào (1) : 
- Vậy có 2 đường thẳng : , 
Bài 10 Viết phương trình tiếp tuyến chung của hai đường tròn : 
	(C1) : (x - 5)2 + (y + 12)2 = 225 và (C2) : (x – 1)2 + ( y – 2)2 = 25
Hướng dẫn: - Ta có (C) với tâm I(5;-12) ,R=15. (C') có J(1;2) và R'=5. Gọi d là tiếp tuyến chung có phương trình : ax+by+c=0 ().
- Khi đó ta có : 
- Từ (1) và (2) suy ra : 
. Thay vào (1) : ta có hai trường hợp :
- Trường hợp : c=a-9b thay vào (1) : 
Suy ra :
- Trường hợp : . Vô nghiệm . ( Phù hợp vì : . Hai đường tròn cắt nhau ) .
Bài 11 Cho đường tròn (C): x2 + y2 – 2x – 6y + 6 = 0 và điểm M (2;4)
Viết phương trình đường thẳng đi qua M cắt đường tròn tại 2 điểm A và B, sao cho M là trung điểm của AB
Hướng dẫn: - Đường tròn (C) : nằm trong hình tròn (C) .
- Gọi d là đường thẳng qua M(2;4) có véc tơ chỉ phương 
- Nếu d cắt (C) tại A,B thì : ( có 2 nghiệm t ) . Vì vậy điều kiện : 
- Gọi M là trung điểm AB thì ta có hệ :
. Thay vào (1) khi áp dụng vi ét ta được :
Bài 12 Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C): x2 + y2 - 2x - 2my + m2 - 24 = 0 có tâm I và đường thẳng D: mx + 4y = 0. Tìm m biết đường thẳng D cắt đường tròn (C) tại hai điểm phân biệt A,B thỏa mãn diện tích tam giác IAB bằng 12.
Hướng dẫn: - (C) : .
- Nếu d : mx +4y=0 cắt (C) tại 2 điểm A,B thì 
- Điều kiện : . Khi đó gọi 
- Khoảng cách từ I đến d = 
- Từ giả thiết : 
- Ta có một phương trình trùng phương , học sinh giải tiếp . 
Bài 13 Viết phương trình đường tròn đi qua hai điểm A(2; 5), B(4;1) và tiếp xúc với đường thẳng có phương trình 3x – y + 9 = 0.
Hướng dẫn: 
 Gọi M là trung điểm AB suy ra M(3;3 ) . d' là đường trung trực của AB thì d' có phương trình : 1.(x-3)-2(y-3)=0 , hay : x-2y+3=0 . 
- Tâm I của (C) nằm trên đường thẳng d' cho nên I(2t-3;t) (*)
- Nếu (C) tiếp xúc với d thì . (1)
- Mặt khác : R=IA=. (2) .
- Thay (2) vào (1) : 
. Thay các giá trị t vào (*) và (1) ta tìm được tọa độ tâm I và bán kính R của (C) .
* Chú ý : Ta có thể sử dụng phương trình (C) : ( có 3 ẩn a,b,c)
- Cho qua A,B ta tạo ra 2 phương trình . Còn phương trình thứ 3 sử dụng điều kiện tiếp xúc của (C) và d : khoảng cách từ tâm tới d bằng bán kính R .
I
M
A
B
H
 Bài 14 Cho đường tròn (C): x2 + y2 – 2x + 4y + 2 = 0. 
Viết phương trình đường tròn (C') tâm M(5, 1) biết (C') 
ắt (C) tại các điểm A, B sao cho .
Hướng dẫn: - Đường tròn (C) :
 .
- Gọi H là giao của AB với (IM). Do đường tròn (C') tâm M 
có bán kính R' = MA . Nếu AB=, thì tam giác 
IAB là tam giác đều , cho nên IH= ( đường cao 
tam giác đều ) . Mặt khác : IM=5 suy ra HM= . 
- Trong tam giác vuông HAM ta có 
- Vậy (C') : .
Bài 15 Trong mÆt ph¼ng víi hÖ täa ®é Oxy cho ®­êng trßn (C) cã ph­¬ng tr×nh (x-1)2 + (y+2)2 = 9 vµ ®­êng th¼ng d: x + y + m = 0. T×m m ®Ó trªn ®­êng th¼ng d cã duy nhÊt mét ®iÓm A mµ tõ ®ã kÎ ®­îc hai tiÕp tuyÕn AB, AC tíi ®­êng trßn (C) (B, C lµ hai tiÕp ®iÓm) sao cho tam gi¸c ABC vu«ng.
Hướng dẫn: 
I(1;-2)
B
C
A
x+y+m=0
- (C) có I(1;-2) và bán kính R=3 . Nếu tam giác ABC vuông góc tại A ( có nghĩa là từ A kẻ được 2 tiếp tuyến 
tới (C) và 2 tiếp tuyến vuông góc với nhau ) khi đó 
ABIC là hình vuông . Theo tính chất hình vuông ta có 
IA= IB(1) .
- Nếu A nằm trên d thì A( t;-m-t ) suy ra : 
. Thay vào (1) :
(2). Để trên d có 
đúng 1 điểm A thì (2) có đúng 1 nghiệm t , từ đó ta có điều 
kiện : .Khi đó (2) có nghiệm kép là :
Bài 16 Trong mặt phẳng toạ độ Oxy cho hai đường thẳng (d1) : 4x - 3y - 12 = 0 và (d2): 4x + 3y - 12 = 0. Tìm toạ độ tâm và bán kính đường tròn nội tiếp tam giác có 3 cạnh nằm trên (d1), (d2), trục Oy.
Hướng dẫn: - Gọi A là giao của 
- Vì (BC) thuộc Oy cho nên gọi B là giao của với Oy : cho x=0 suy ra y=-4 , B(0;-4) và C là giao của với Oy : C(0;4 ) . Chứng tỏ B,C đối xứng nhau qua Ox , mặt khác A nằm trên Ox vì vậy tam giác ABC là tam giác cân đỉnh A . Do đó tâm I đường tròn nội tiếp tam giác thuộc Ox suy ra I(a;0). 
- Theo tính chất phân giác trong : 
. Có nghĩa là I() 
- Tính r bằng cách : .
Bài 17 Trong mặt phẳng Oxy , cho hai đường tròn : và cắt nhau tại A(2;3).Viết phương trình đường thẳng đi qua A và cắt theo hai dây cung có độ dài bằng nhau
Hướng dẫn: 
- Từ giả thiết : 
- Gọi đường thẳng d qua A(2;3) có véc tơ chỉ phương 
- d cắt tại A, B : 
. Tương tự d cắt tại A,C thì tọa độ của A,C là nghiệm của hệ : 
- Nếu 2 dây cung bằng nhau thì A là trung điểm của A,C . Từ đó ta có phương trình :
Suy ra : . Vậy có 2 đường thẳng : d: x-2=0 và d': 2x-3y+5=0
Bài 18 Trong mặt phẳng với hệ tọa độ Oxy, cho điểm E(-1;0) và đường tròn 
( C ): x2 + y2 – 8x – 4y – 16 = 0.
 Viết phương trình đường thẳng đi qua điểm E cắt ( C ) theo dây cung MN có độ dài ngắn nhất.
Hướng dẫn: - 
- Nhận xét : P/(M,C)=1+8-16=-7<0 suy ra E nằm trong (C) 
- Gọi d là đường thẳng qua E(-1;0) có véc tơ chỉ phương 
- Đường thẳng d cắt (C) tại 2 điểm M,N có tọa độ là nghiệm của hệ :
. (1)
- Gọi M(-1+at;bt),N( -1+at';bt') với t và t' là 2 nghiệm của (1). Khi đó độ dài của dây cung MN 
- . Xét hàm số f(t)=
- Tính đạo hàm f'(t) cho bằng 0 , lập bảng biến thiên suy ra GTLN của t , từ đó suy ra t ( tức là suy ra tỷ số a/b ) ). Tuy nhiên cách này dài 
* Chú ý : Ta sử dụng tính chất dây cung ở lớp 9 : Khoảng cách từ tâm đến dây cung càng nhỏ thì dây cung càng lớn 
- Gọi H là hình chiếu vuông góc của I trên đường thẳng d bất kỳ qua E(-1;0). Xét tam giác vuông HIE ( I là đỉnh ) ta luôn có : . Do đó IH lớn nhất khi HE=0 có nghĩa là H trùng với E . Khi đó d cắt (C) theo dây cung nhỏ nhất . Lúc này d là đường thẳng qua E và vuông góc với IE cho nên d có véc tơ pháp tuyến , do vậy d: 5(x+1)+2y=0 hay : 5x+2y+5=0 .
Bài 19 Trong mặt phẳng Oxy, cho đường tròn (C): x2 + y2 – 6x + 2y – 15 = 0. Tìm tọa độ điểm M trên đường thẳng d: 3x – 22y – 6 = 0, sao cho từ điểm M kẻ được tới (C) hai tiếp tuyến MA, MB (A, B là các tiếp điểm) mà đường thẳng AB đi qua điểm C (0;1).
Hướng dẫn: M
A
B
I(3;-1)
H
C(0;1)
3x-22y-6=0
- (C) : , có I(3;-1) 
và R=5 . 
- Gọi là 2 tiếp điểm của 2 tiếp tuyến 
kẻ từ M . 
- Gọi M
- Hai tiếp tuyến của (C) tại A,B có phương trình là :
- và :
- 
- Để 2 tiếp tuyến trở thành 2 tiếp tuyến kẻ từ M thì 2 
tiếp tuyến phải đi qua M ;
- và 
- 
Từ (3) và (4) chứng tỏ (AB) có phương trình là : 
- Theo giả thiết thì (AB) qua C(0;1) suy ra :
- Kết hợp với (*) ta có hệ : 
Bài 20 Trong mp Oxy, cho đường tròn (C): x2 + y2 – 6x + 2y + 6 = 0 và điểm P(1;3).
a.Viết phương trình các tiếp tuyến PE, PF của đường tròn (C), với E, F là các tiếp điểm.
b.Tính diện tích tam giác PEF.
Hướng dẫn: I(3;-1)
E
F
P(1;3)
O
x
y
H
- (C): 
- Giả sử đường thẳng qua P có véc tơ pháp tuyến 
Hay : ax+by-(a+3b)=0 (*).
- Để d là tiếp tuyến của (C) thì khoảng cách từ 
tâm I đến d bằng bán kính :
-Ta có : PI=2, PE=PF=. 
 Tam giác IEP đồng dạng với IHF suy ra :
Bài 21 Trong mpOxy, cho 2 đường thẳng d1: 2x + y - 1 = 0, d2: 2x - y + 2 = 0. Viết pt đường tròn (C) có tâm nằm trên trục Ox đồng thời tiếp xúc với d1 và d2.
Hướng dẫn: - Gọi I(a;0) thuộc Ox . Nếu (C) tiếp xúc với 2 đường thẳng thì : 
. Từ (1) : a=, thay vào (2) : R=
Bài 22 Cho đường tròn (C): x2 + y2 - 2x - 4y + 3 = 0. Lập pt đường tròn (C’) đối xứng với (C) qua đường thẳng D: x - 2 = 0
Hướng dẫn: Ta có (C): 
- Gọi J là tâm của (C') thì I và J đối xứng nhau qua d : x=2 suy ra J(3;2) và (C) có cùng bán kính R . Vậy (C'): đối xứng với (C) qua d .
Bài 23 Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d: x + y - 3 = 0 và 2 điểm A(1; 1), B(-3; 4). Tìm tọa độ điểm M thuộc đường thẳng d sao cho khoảng cách từ M đến đường thẳng AB bằng 1.
Hướng dẫn: - M thuộc d suy ra M(t;3-t) . Đường thẳng (AB) qua A(1;1) và có véc tơ chỉ phương 
- Theo đầu bài : 
* Chú ý : 
Đường thẳng d' song song với (AB) có dạng : 3x+4y+m=0 . Nếu d' cách (AB) một khoảng bằng 1 thì h(A,d')=1
. Tìm giao của d' với d ta tìm được M .
Bài 24 Trong hệ trục 0xy, cho đường tròn (C): x2+y2 -8x+12=0 và điểm E(4;1). Tìm toạ độ điểm M trên trục tung sao cho từ M kẻ được 2 tiếp tuyến MA, MB đến (C), với A,B là các tiếp điểm sao cho E thuộc đường thẳng AB
Hướng dẫn: y
x
I(4;0)
O
1
E(4;1)
A
B
M
d'
- Đường tròn (C) : 
- Gọi M(0;a) thuộc Oy .
- Tiếp tuyến tại A và B có phương trình là :
- Để thỏa mãn 2 tiếp tuyến này cùng qua M(0;a)
.
 Chứng tỏ (AB) có phương trình : -4(x-4)+ay=4 
- Nếu (AB) qua E(4;1) : -4(0)+a.1=4 suy ra : a=4 
Vậy trên Oy có M(0;4 ) thỏa mãn .
Bài 25 Vieát phöông trình ñöôøng troøn (C ) coù baùn kính R = 2 tieáp xuùc vôùi truïc hoaønh vaø coù taâm I naèm treân ñöôøng thaúng (d) : x + y – 3 = 0.
Hướng dẫn: - Tâm I nằm trên d suy ra I(t;3-t) . Nếu (C) tiếp xúc với Ox thì khoảng cách từ I đến Ox bằng bán kính R=2 : 
- Như vậy có 2 đường tròn : .
Bài 26 Trong maët phaúng Oxy cho ñöôøng troøn (C) coù phöông trình : 
 x2 + y2 – 2x – 6y + 6 = 0. 
a. Vieát phöông trình ñöôøng thaúng ñi qua M(2 ; 4) caét ñöôøng troøn (C) taïi 2 ñieåm A, B sao cho M laø trung ñieåm ñoaïn AB.
b. Vieát phöông trình tieáp tuyeán cuûa (C) sao cho tieáp tuyeán aáy song song vôùi ñöôøng thaúng coù phöông trình : 2x + 2y – 7 = 0.
c. Chöùng toû ñöôøng troøn (C) vaø ñöôøng troøn (C ’) : x2 + y2 – 4x – 6y + 4 = 0 tieáp xuùc nhau. Vieát phöông trình tieáp tuyeán chung cuûa chuùng taïi tieáp ñieåm
Hướng dẫn: - (C) : . 
a. Gọi A(x;y) thuộc (C) suy ra (1) , B đối xứng với A qua M suy ra B(4-x;8-y) . Để đảm bảo yêu cầu bài toán thì B thuộc (C) : (2).
- Từ (1) và (2) ta có hệ : 
- Lấy (3) -(4) ta có phương trình : 4x+4y-24=0 , hay : x+y-6=0 . Đó chính là đường thẳng cần tìm .
b. Gọi d' là đường thẳng // với d nên nó có dạng : 2x+2y+m=0 (*) . Để d' là tiếp tuyến của (C) thì : 
c. (C'): 
- Ta có : II'=1 , R'-R=1 . Chứng tỏ hai đường tròn tiếp xúc trong với nhau .
- Tìm tọa độ tiếp điểm : . Thay vào phương trình đầu của hệ : .
- Tiếp tuyến chung qua M và vuông góc với IJ suy ra d': 1(x-1)=0 hay : x-1=0 .
Bài 27 Trong maët phaúng Oxy cho (E) coù phöông trình : 4x2 + 9y2 = 36.
a. . Cho 2 ñöôøng thaúng (D) : ax – by = 0 vaø (D’) : bx + ay = 0 (a2 + b2 > 0). Tìm giao ñieåm E, F cuûa (D) vôùi (E) vaø giao ñieåm P, Q cuûa (D’) vôùi (E). Tính dieän tích töù giaùc EPFQ theo a, b.
b. Chứng minh rằng MPFQ luôn ngoại tiếp một đường tròn cố định ? Viết phương trình đường tròn cố định đó.
c. Cho ñieåm M(1 ; 1). Vieát phöông trình ñöôøng thaúng ñi qua M vaø caét (E) taïi hai ñieåm A, B sao cho M laø trung ñieåm cuûa ñoaïn thaúng AB
Hướng dẫn: a. Hai đường thẳng (D) và (D') vuông góc nhau . 
- (D) giao với (E) tại E,F có tọa độ là nghiệm của hệ : 
- Tương tự (D') cắt (E) tại P,Q với tọa độ là nghiệm: 
- Tính diện tích tam giác EPFQ ; 
Bài 28 Trong maët phaúng toïa ñoä Oxy, cho hoï ñöôøng thaúng phuï thuoäc tham soá a : 
(x – 1)cosa + (y – 1)sina – 1 = 0
a. Tìm taäp hôïp caùcñieåm cuûa maët phaúng khoâng thuoäc baát kyø ñöôøng thaúng naøo cuûa hoï.
b. Chöùng minh moïi ñöôøng thaúng cuûa hoï ñeàu tieáp xuùc vôùi moät ñöôøng troøn coá ñònh.
Hướng dẫn: b. Gọi là điểm cố định . Khoảng cách từ I đến d có giá trị là :
- Với kết quả trên chứng tỏ d luôn tiếp xúc với đường tròn (C) có tâm I và bán kính bằng 1 ( Không phụ thuộc vào . (C): 
Bài 29 Cho hai điểm A(1;1), B(4;-3) và đường thẳng d : x-2y-1=0. 
a. Tìm tọa độ điểm C trên d sao cho khoảng cách từ C đến đường thẳng AB=6( ĐHKB-04)
b. Tìm tọa độ trực tâm và tâm đường tròn ngoại tiếp tam giác OAB ?( ĐHKA-2004) 
Hướng dẫn: 
a/ (AB) qua A(1;1) có 
- C thuộc : x-2y-1=0 suy ra C(2t+1;t ) do đó : 
b/ - Đường thẳng qua O vuông góc với AB có phương trình : 3x-4y=0.
- Đường thẳng qua B và vuông góc với OA có phương trình : (x-4)+(y+3)=0.
- Đường thẳng qua A và vuông góc với OB có phương trình : 4(x-1)-3(y-1)=0 
hay : 4x-3y-1=0 
- Vậy tọa độ trực tâm H là nghiệm : 
- Giả sử đường tròn ngoại tiếp tam giác (C): 
- (C) qua O(0;0) suy ra c=0 (1)
- (C) qua A(1;1) suy ra : 2-2a-2b=0 , hay : a+b=1 (2)
- (C) qua B(4;-3) suy ra : 25-8a+6b=0 , hay : 8a-6b=25 (3) 
- Từ (2) và (3) ta có hệ : 
- Vậy (C) : 
Bài 30 Trong mặt phẳng Oxy cho điểm M(2;-1) và đường tròn (1) .Hãy viết phương trình đường tròn có bán kính bằng 4 và cắt đường tròn theo dây cung qua M có độ dài nhỏ nhất .
Hướng dẫn: Gọi có tâm I'(a;b) suy ra :
Lấy (1) -(2) ta được : ( chính là đường thẳng trục đẳng phương )
Dây cung của hai đường tròn nằm trên đường thẳng này .
Ví dây cung qua M(2;-1) lên ta có : 
Bài 31 . Trong mặt phẳng với hệ tọa độ Oxy cho hai đường thẳng:, và điểm A(-2 ; 1). Viết phương trình đường tròn có tâm thuộc đường thẳng , đi qua điểm A và tiếp xúc với đường thẳng ’. 
Hướng dẫn: Tâm I của đường tròn thuộc nên I(-3t – 8; t)
Theo yc thì k/c từ I đến ’ bằng k/c IA nên ta có 
Giải tiếp được t = -3 
Khi đó I(1; -3), R = 5 và pt cần tìm: (x – 1)2 + (y + 3)2 = 25.
Bài 32 . Trong mặt phẳng với hệ tọa độ Oxy cho đường tròn hai đường tròn : cùng đi qua M(1; 0).
 Viết phương trình đường thẳng qua M cắt hai đường tròn lần lượt tại A, B sao cho MA= 2MB.
Hướng dẫn: + Gọi tâm và bán kính của (C), (C’) lần lượt là I(1; 1) , I’(-2; 0) và , đường thẳng (d) qua M có phương trình .
+ Gọi H, H’ lần lượt là trung điểm của AM, BM.
Khi đó ta có: ,
Dễ thấy nên chọn .
Kiểm tra điều kiện rồi thay vào (*) ta có hai đường thẳng thoả m ãn.
Bài 33 . Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C): x2 + y2 - 2x - 2my + m2 - 24 = 0 có tâm I và đường thẳng D: mx + 4y = 0. Tìm m biết đường thẳng D cắt đường tròn (C) tại hai điểm phân biệt A,B thỏa mãn diện tích tam giác IAB bằng 12.
Hướng dẫn:
Đường tròn (C) có tâm I(1; m), bán kính R = 5.
I
A
B
D
H
5
Gọi H là trung điểm của dây cung AB. 
Ta có IH là đường cao của tam giác IAB.
IH = 
Diện tích tam giác IAB là 
Û 
Bài 34 . Cho đường tròn (C): x2 + y2 – 2x + 4y + 2 = 0. 
Viết phương trình đường tròn (C') tâm M(5, 1) biết (C') cắt (C) tại các điểm A, B sao cho .
Hướng dẫn: 
Phương trình đường tròn (C): x2 + y2 – 2x + 4y + 2 = 0 có tâm I(1, –2) 
Đường tròn (C') tâm M cắt đường tròn (C) tại A, B nên AB ^ IM tại trung điểm H của đoạn AB. Ta có . Có 2 vị trí cho AB đối xứng qua tâm I.
Gọi A'B' là vị trí thứ 2 của AB, Gọi H' là trung điểm của A'B'
Ta có: , 
Vậy có 2 đường tròn (C') thỏa ycbt là: (x – 5)2 + (y – 1)2 = 13 hay (x – 5)2 + (y – 1)2 = 43
Bài 35 Trong (Oxy) cho đường tròn (C): và . Tìm trên (P) các điểm M mà từ đó kẻ được 2 tiếp tuyến đến (C) và 2 tiếp tuyến đó tạo với nhau một góc 
Hướng dẫn: Gọi M. d là đường thẳng tiếp tuyến của (P) tại M thì d có phương trình : . Để d là tiếp tuyến kẻ từ M đến (C) thì điều kiện cần và đủ là : 
Bài 36 Trong (Oxy) cho đ. thẳng d: 3x-y+5=0 và đường tròn (C): . Tìm điểm M thuộc (C) và điểm N thuộc d sao cho MN có độ dài nhỏ nhất ?
Hướng dẫn: (C) :
- Gọi d' //d thì d': 3x-y+m=0 . d' tiếp xúc với (C) tại M ( M là điểm cách d nhỏ nhất ) , khi đó : 
d'
d'
d:3x-y+5=0
M
M
N
N'
I(-1;3)
Giả sử N' thuộc d ta luôn có : . Dấu bằng chỉ xảy ra khi N' trùng với N . Vậy ta chỉ cần lập đường thẳng qua I(-1;3) và vuông góc với d suy ra đường thẳng . Khi đó cắt d' tại 2 điểm : .
Và .
Do vậy ta tìm được 2 điểm M : , và . Tương tự cắt d tại N có tọa độ là nghiệm :
 . Ta chọn M bằng cách tính , sau đó so sánh : Nếu thì M là . Còn thì M là .
Bài 37 Trong (Oxy) cho và điểm . Tìm trên (C) điểm N sao cho MN có độ dài lớn nhất ?
Hướng dẫn: (C) viết dưới dạng tham số : 
Khi đó : 
. Vì : ,
 thì (*) trở thành : 
 Dấu đẳng thức xảy ra khi : 
Do vậy : 
Tương tự : 
Bài 38 Trong (Oxy) cho hai điểm 
a/ Chứng tỏ tam giác OAB là tam giác đều 
b/ Chứng minh rằng tập hợp các điểm M sao cho : là một đường tròn (C). 
c/ Chứng tỏ (C) là đường tròn ngoại tiếp tam giác OAB. 
Hướng dẫn: a/ Ta có : . Chứng tỏ OAB là tam giác đều .
b/ Gọi M(x;y) thì đẳng thức giả thiết cho tương đương với biểu thức :
Ta có : 
. Chứng tỏ là đường tròn (C) có tâm 
c/ Thay tọa độ O,A,B vào (1) ta thấy thỏa mãn , chứng tỏ (C) là đường tròn ngoại tiếp tam giác OAB.
Bài 39 Trong mặt phẳng tọa độ Oxy cho đường tròn , đường thẳng . Tìm để cắt tại A và B sao cho diện tích tam giác ABO lớn nhất.
Hướng dẫn: *(C) có tâm O(0;0) , bán kính R=1 *(d) cắt (C) tại hai điểm phân biệt 
*Ta có Từ đó diện tích tam giác AOB lớn nhất khi và chỉ khi 
Bài 40 Trong mặt phẳng với hệ toạ độ Oxy, cho đường tròn (C) có phương trình: .
 Tia Oy cắt (C) tại A. Lập phương trình đường tròn (C’), bán kính R’ = 2 và tiếp xúc ngoài với (C) tại A.
Hướng dẫn: A(0;2), I(-2 ;0), R= 4, gọi (C’) có tâm I’ Pt đường thẳng IA : , => I’(), (C’): 
Bài 41 Cho đường tròn (C): x2 + y2 – 2x – 6y + 6 = 0 và điểm M (2;4)
a) Viết phương trình đường thẳng đi qua M cắt đường tròn tại 2 điểm A và B, sao cho M là trung điểm của AB.
b) Viết phương trình các tiếp tuyến của đường tròn, biết tiếp tuyến có hệ số góc k = -1.
Hướng dẫn: a. (C) : I(1; 3), R= 2, A, B , M là trung điểm AB => Đường thẳng d cần tìm là đg thẳng AB; d đi qua M có vectơ pháp tuyến là => d: x + y - 6 =0
 b. Đg thẳng tiếp tuyến có dạng : y = - x + m ó x + y – m =0 (d’)d’ tiếp xúc với (C) Pt tiếp tuyến : 
Bài 42 Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C): x2 + y2 - 2x - 2my + m2 - 24 = 0 có tâm I và đường thẳng D: mx + 4y = 0. Tìm m biết đường thẳng D cắt đường tròn (C) tại hai điểm phân biệt A,B thỏa mãn diện tích tam giác IAB bằng 12.
Hướng dẫn: Đường tròn (C) có tâm I(1; m), bán kính R = 5.
Gọi H là trung điểm của dây cung AB. 
I
A