Ôn thi tốt nghiệp THPT Toán 217 - Khảo sát hàm số và ứng dụng - Phạm Bắc Tiến

Ôn thi TN THPT QG 2017 1 GV: Phạm Bắc Tiến−0939319183 
KHẢO SÁT HÀM SỐ VÀ CÁC ỨNG DỤNG 
I/ HÀM BẬC BA: y = f(x) = ax3 + bx2 + cx + d (a ≠ 0) 
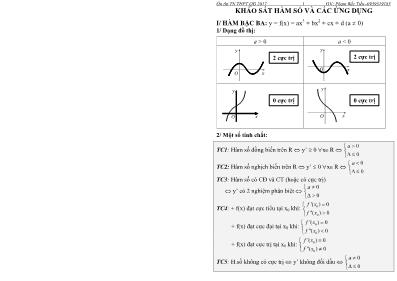
1/ Dạng đồ thị: 
2 cực trị 2 cực trị
0 cực trị 0 cực trị
a > 0 a < 0 
2/ Một số tính chất: 
0
0
a >⎧⎨TC1: Hàm số đồng biến trên R ⇔ y’ ≥ 0 ∀x∈R ⇔ Δ ≤⎩ 
TC2: Hàm số nghịch biến trên R ⇔ y’ ≤ 0 ∀x∈R ⇔ 0
0
a <⎧⎨Δ ≤⎩
TC3: Hàm số có CĐ và CT (hoặc có cực trị) 
0a
0
≠⎧ ⇔ y’ có 2 nghiệm phân biệt ⇔ ⎨Δ >⎩
0
0
'( ) 0
''( ) 0
f x
f x
=⎧⎨ >⎩
 TC4: + f(x) đạt cực tiểu tại x0 khi: 
0
0
'( ) 0
''( ) 0
f x
f x
=⎧⎨ + f(x) đạt cực đại tại x0 khi: <⎩
0
0
'( ) 0
''( ) 0
f x
f x
=⎧⎨ + f(x) đạt cực trị tại x0 khi: ≠⎩
0
0
a ≠⎧⎨TC5: H.số không có cực trị ⇔ y’ không đổi dấu ⇔ Δ ≤⎩ 
GV: Phạm Bắc Tiến−0995095121 2 Ôn thi TN THPT QG 2017 Ôn thi TN THPT QG 2017 31 GV: Phạm Bắc Tiến−0939319183 
a>0, 2 cực trị 
xCĐ < xCT 
a<0, 2 cực trị 
xCT < xCĐ 
d: y =h(m) d: y =h(m)
a>0, 3 cực trị 
xCĐ= 0 
a>0, ab>0 
Hoặc a>0, b = 0 
a0 
Hoặc a<0, b = 0 
TC6: ĐT h.số tiếp xúc với trục hoành ⇔hệ pt ( ) 0
'( ) 0
f x
f x
=⎧⎨ =⎩ có nghiệm 
⇒ 11
2 22
d
dV S
= = 2 ⇒ C SV
Câu 41: Trong không gian, cho hình chữ nhật ABCD có 1AB = và TC7: Tiếp tuyến của đồ thị hàm bậc ba có hệ số góc nhỏ nhất nếu 
a>0 và có hệ số góc lớn nhất nếu a < 0. 
2AD = . Gọi M, N lần lượt là trun điểm của A BC a
chữ nhật đó xung quanh trục MN được mộ ụ
g D và . Qu y hình 
, ta t hình tr . Tính diện tích 
n phần tpS trụ đó. 
A. 4S
toà của hình TC8: Bài toán biện luận số nghiệm của pt f(x) = h(m) (*) 
Trong đó (C): f(x) = ax3 + bx2 + cx + d (a ≠ 0) có 2 cực trị. 
-3 -2 -1 1 2 3
-3
-1
1
2
3
y
-2
x
-3 -2 -1 1 2
-3
-2
-1
1
2
3
3
x
y
y (*) có đúng 1 nghiệm ⇔ h(m) fCĐ 
y (*) có 2 nghiệm ⇔ h(m) = fCT ∨ h(m) = fCĐ 
y (*) có 3 nghiệm phân biệt ⇔ fCT < h(m) < fCĐ 
II/ HÀM TRÙNG PHƯƠNG: y = ax4 + bx2 + c (a ≠ 0) 
1/ Dạng đồ thị: 
a<0, 3 cực trị 
xCT = 0 
A
G
C 
G 
I ’
S
B 
Δ
H
tp π= B. 2tpS π C. 6S= tp π D. 10tpS= π= 
Câu 42: ng 
nh ối cầu ngoại tiếp hình chóp đã cho. 
h = AB = 1, R = AM = 1 ⇒ Stp = 2πRh + 2πR2 = 4π ⇒ A 
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằ
1, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc 
với đáy. Tí thể tích V của kh
A. 5 15
18
V π= B. 5 15
54
V π= C. 4 3
27
V π= D. 5
3
V π= 
Rcầu = IA = 
2 2
2 2 3 3
3 6
AG IG
⎛ ⎞ ⎛ ⎞+ = +⎜ ⎟ ⎜ ⎟⎜ ⎟ ⎜ ⎟⎝ ⎠ ⎝ ⎠
 = 15
6
⇒ V = 4 3 = 5 15
54
π
3
πR ⇒ B 
GV: Phạm Bắc Tiến−0995095121 30 Ôn thi TN THPT QG 2017 Ôn thi TN THPT QG 2017 3 GV: Phạm Bắc Tiến−0939319183 
fCĐ
d: y =h(m) d: y =h(m)
H.1 H.2
y fCT
y fCĐ
# CHÚ Ý: Đồ thị hàm trùng phương nhận trục Oy làm trục đối xứng. a/ Mặt cầu ngoại tiếp hình chóp SABCD có đường kính là: SC 
 b/ Mặt cầu qua 7 điểm A, B, C, D, H, I, K có đường kính là: AC 
Dạng 2:
2/ Một số tính chất: 
 Xác định tâm của đường tròn ngoại tiếp hình chóp TC1: Hàm số luôn có cực trị ∀a≠ 0 
# CHÚ Ý: Hàm số y = ax4 + bx2 + c có đúng một cực trị khi: y Xác định tâm O của đường tròn ngoại tiếp đáy hình chóp. 
Hoặc ab>0, ví dụ: y = x4 + 2x2 − 4, y = −x4 − 2x2 + 2 y Qua O dựng đường thẳng Δ vuông góc với đáy hình chóp. 
 y Dựng mp(P) là mặt trung trực của một cạnh bên. Hoặc a ≠ 0, b = 0, ví dụ: y = x4 − 4, y = −x4 + 2 
 Gọi I = Δ ∩ (P) ⇒ I là tâm mặt cầu ngoại tiếp hình chóp. TC2: Hàm số có CĐ và CT (hoặc có 3 cực trị) ⇔ ab<0 
Dạng 3: Tính diện tích mặt cầu, hình nón, hình trụ, diện tích thiết diện. 
 Tính thể tích khối cầu, khối nón, khối trụ. 
Phương pháp: Áp dụng công thức tính tương ứng 
ại A, Câu 39: Trong không gian, cho tam giác ABC vuông t AB a= và 
3AC a= . Tính độ dài đường sinh l của hình nón, nhận được khi quay 
tam giác ABC xung quanh trục AB. 
A. l a= B. 2l a= C. 3l a= D. 2l a= 
h = AB = a, R = AC = a 3 ⇒ l = 2 2h R+ = 2a ⇒ D 
Câu 40: m tôn hình chữ nhật kích thước 50cm x 240cm, 
ng 50cm, 
theo hai cá
ủa thùng. 
* Cách 2: C tôn ban ấm ằ nhau i gò i 
ua một thùn
hể 
Từ một tấ
người ta làm các thùng đựng nước hình trụ có chiều cao bằ
ch sau (xem hình minh họa dưới đây): 
* Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh c
ắt tấm đầu thành hai t b ng , rồ mỗ
tấm đó thành mặt xung q nh của g. 
Kí hiệu là thể tích của thùng gò o cách 1 và 1V được the 2V là tổng t
tích của hai thùng gò được theo 
cách 2. Tính tỉ số 1V 
2V
A. 1 1
2
V
V
= B. 
2
1 1V
V2
= 
C. 1
2
2V
V
= D. 1
2
4V
V
= 
C1: Thùng có bá nh n kí đáy R1 = 
120
π ⇒ Sd1 = π.
2120
π
⎛ ⎞⎜ ⎟⎝ ⎠ = 
2120
π 
C2: Thùng có bán kí đáy Rnh 2 = 
60
π ⇒ Sd2 = π.
260
π
⎛ ⎞⎜ ⎟⎝ ⎠ = 
260
π 
a<0, 3 cực trị 
 xCT = 0 a>0, 3 cực trị 
 xCĐ = 0 
fCT
TC3: Đ.thị hsố cắt trục hoành tại 4 điểm phân biệt⇔ 
2 4 0
0
0
b ac
bS
a
cP
a
⎪Δ = − >⎪⎪ = − >⎨⎪⎪ = >⎪⎩
⎧
TC4: Bài toán biện luận số nghiệm của pt f(x) = h(m) (*) 
Trong đó (C): f(x) = ax4 + bx2 + c (a ≠ 0) có 3 cực trị. 
y
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y (*) vô nghiệm ⇔ h(m) fCĐ (H.2) 
y (*) có 2 nghiệm phân biệt 
⇔ (H.1) Hoặc (H.2) ( ) (0)h m f>⎡ ⎡
( ) CTh m f
⎢ =⎣
( ) (0)
( ) CD
h m f
h m f
<
⎢ =⎣
y (*) có 3 nghiệm phân biệt ⇔ h(m) = f(0) 
y (*) có 4 nghiệm phân biệt ⇔ fCT < h(m) < fCĐ 
TC5: + f(x) đạt cực tiểu tại x0 khi: 0
0''( ) 0f x
'( ) 0f x =⎧ ⎨ >⎩
0
0
'( ) 0
''( ) 0
f x
f x
=⎧⎨ + f(x) đạt cực đại tại x0 khi: <⎩
0
0
'( ) 0
''( ) 0
f x
f x
=⎧⎨ + f(x) đạt cực trị tại x0 khi: ≠⎩
GV: Phạm Bắc Tiến−0995095121 4 Ôn thi TN THPT QG 2017 Ôn thi TN THPT QG 2017 29 GV: Phạm Bắc Tiến−0939319183 
III/ HÀM NHẤT BIẾN: ax by
cx d
+= + (c ≠ 0, ad − bc ≠ 0) 
1/ Khảo sát hàm số: 
y TXĐ: D = R \ d
c
⎧ ⎫−⎨ ⎬⎩ ⎭ 
y y’ = 2bcd
−
+( )
ad
cx
Hàm số đồng biến (hay nghịch biến) trên (−∞; d
c
− ), ( d
c
− ;+∞) 
y Tiệm cận đứng: x = d
c
− ; y Tiệm cận ngang: y = a
c
y Bảmg biến thiên: 
 x −∞ d
c
− +∞ x −∞ d
c
− +∞ 
 y’ + + y’ − − 
 y +∞ a
c
 y a
c
 −∞ 
 a
c
 −∞ −∞ a
c
y Đồ thị h.số nhận giao điểm của hai tiệm cận làm tâm đối xứng. 
2/ Một số tính chất của hàm nhất biến: 
TC1: Hàm số đồng biến (nghịch biến) trên từng khoảng xác định 
 ⇔ y’ > 0 (y’ < 0) ∀x∈D 
TC2: M∈(C) cách đều 2 trục tọa độ ⇔ ax b x
cx d
+ =+ 
TC3: M∈(C) sao cho d(M,TCĐ) + d(M,TCĐ) = d nhỏ nhất. 
⇔ adcx d
cx
+ = bc
d
−
+ ⇒ x ⇒ y ⇒ M 
ad − bc > 0 ad − bc < 0 
a b
c d
O Δ 
a H>R ⇔ (O,Δ)∩(C)=∅ ⇒ Δ∩S(O;R)=∅. 
Ta nói Δ không cắt S(O;R). 
b/ OH=R ⇔ (O,Δ)∩(C)=H ⇒ Δ∩S(O;R)=H. 
/ O
H c/ OH<R ⇔ (O,Δ)∩(C)={A,B} 
⇒ Δ∩S(O;R)={A, B}. Đặc biệt, khi H≡O thì AB = 2R. 
Ta nói Δ tiếp xúc với mặt cầu S(O;R) tại H. 
Điểm H gọi là tiếp điểm, Δ gọi là tiếp tuyến. (C)
4/ Mặt cầu ngoại tiếp hình chóp: Mặt cầu gọi là ngoại tiếp một hình 
chóp nếu nó đi qua tất cả các đỉnh của hình chóp đó. Chú ý rằng một 
hình chóp có mặt cầu ngoại tiếp khi và chỉ khi đáy của nó là 1 đa giác 
nội tiếp được. 
5/ Diện tích mặt cầu, thể tích khối cầu: 
S 
B 
C A 
H 
K 
 Mặt cầu có bán kíy nh R có diện tích là S = 4πR2. 
 y Thể tích khối cầu có bán kính R có thể tích là: V = 4
3
πR3. 
CÁC DẠNG TOÁN THƯỜNG GẶP 
Dạng 1: Chứng minh nhiều điểm cùng nằm trên một mặt cầu 
P ng pháp: Chỉ ra trong các điểm đó có 2 điểm chươ ố định mà các 
đ còn lại cùng nhìn 2 điểm đó dưới một góc vuông hoiểm ặc chứng 
minh các điểm đó cùng cách đều một điểm cố định cho trước một 
khoảng không đổi. 
 1/ Hình chóp SABC, ΔABC vuông tại B; H, K l ượt là hình ần l
chiếu của A trên SB, SC. Khi đó: 
 a/ Mặt cầu ngoại tiếp hình chóp SABC có đường kí : SC nh là
 b/ Mặt cầu qua 5 điểm A, B, C, H, K có đường kính là: AC 
2/ Hình chóp SABCD, đáy ABCD hình chữ nhật (hoặc hình vuông); 
H, K lần lượt là hình chiếu của A trên SB, SC, I=(AHK)∩SC. Khi đó: 
S
I
D
CB
A
K
H
GV: Phạm Bắc Tiến−0995095121 28 Ôn thi TN THPT QG 2017 
 III. MẶT CẦU:
1/ M t cầu, khối cầu: ặ
a/ Mặt cầu: Quay đường tròn 
đư uờng kính AB q anh đường kính 
AB ta được 1 hình gọi là mặt cầu. 
 y Tâm O của mặt cầu là trung điểm của đoạn AB. Mặt cầu có tâm 
O, bán kính R kí hiệu là S(O;R) 
 y Trong không gian, tập hợp các điểm nhìn đoạn thẳng AB dưới 
một góc vuông là mặt cầu đường kính AB. 
b/ Khối cầu: S(O; R) = {M/ OM ≤ R} 
c/ Cho mặt cầu S(O;R) và điểm A. Khi đó: 
 OA > R ⇔ A nằm ngoài my ặt cầu S(O;R). 
 y OA = R ⇔ A∈S(O;R). 
 y OA < R ⇔ A nằm trong mặt cầu S(O;R). 
2/ Vị trí tương đối giữa mặt cầu và mặt phẳng: 
 Cho mặt cầu S(O;R) và mp(P). Gọi H là hình chiếu của O trên 
mp(P). Khi đó: 
a/ OH > R ⇔ (P) ∩ S(O;R) = ∅. Ta nói (P) không cắt S(O;R). 
b/ OH = R ⇔ (P) ∩ S(O;R) = H. Ta nói (P) tiếp xúc với mặt cầu 
S(O;R) tại H. Điểm H gọi là tiếp điểm, mp(P) gọi là tiếp diện. 
c/ OH < R ⇔ (P) ∩ S(O;R) = (C) với (C) là đường tròn có tâm H và 
bán kính 2 2r R OH= − . 
 Đặc biệt, khi H≡O (OH = 0) thì mp(P) gọi là mặt phẳng kính và 
đường tròn (C) có tâm O, bán kính R gọi là đường tròn lớn của mặt 
cầu S(O;R). 
3/ Vị trí tương đố a mặt cầu và đường thẳng: 
 Cho O; R) và 
i giữ
mặt cầ đi qua O. Gọi H là u S( đường thẳng Δ không 
hình chiếu của O trên Δ, (C)= (O,Δ) ∩ S(O;R). Khi đó: 
A B O M
O 
H 
O 
H 
O R 
r H
Ôn thi TN THPT QG 2017 5 GV: Phạm Bắc Tiến−0939319183 
IV/ MỘT SỐ BÀI TOÁN VỀ KHẢO SÁT HÀM SỐ: 
Bài toán 1: Tìm điều kiện để 2 đồ thị (C1): y = f(x) và (C2): y = g(x) 
cắt nhau tại k điểm phân biệt. 
Bước 1: Pt hoành độ giao điểm của (C1) và (C2) là f(x) = g(x) (1). 
Bước 2: (C1) và (C2) cắt nhau tại k điểm phân biệt ⇔ (1) có k nghiệm 
phân biệt. Từ đó suy ra kết luận của bài toán. 
Bài toán 2: Tiếp tuyến 
Dạng 1: Viết pttt của đồ thị (C): y = f(x) tại điểm M(x0;y0)∈(C) 
Pt tiếp tuyến của (C) tại điểm M là: y = f’(x0)(x − x0) + y0. 
f’(x0) = 0( ( ))x xf xdx
d ; y0 = f(x0) =
Dạng 2: Viết pttt của đồ thị (C): y = f(x) biết hệ số góc k. 
B1: Dạng tiếp tuyến y = kx + b 
B2: Giải pt f’(x) = k ⇒ xtt 
B3: Tính b = f(x) − kx CALC xtt = ⇒ b ⇒ tt: y = kx + b 
‰ CHÚ Ý: +Nếu tiếp tuyến d//Δ: y = kx+m 
 ⇒ d: y = kx + b, b ≠ m hoặc kd = kΔ 
 + Nếu tiếp tuyến d⊥Δ: y = kx + m 
 ⇒ d: y = 1
k
x + b hoặc kd.kΔ = −1 −
Dạng 3: Tìm M∈(C): y=f(x) biết tiếp tuyến của (C) tại M có hsgóc k. 
Giải pt f’(x) = k ⇒ x ⇒ y ⇒ M(x;y) 
‰ CHÚ Ý: Nếu tiếp tuyến tại M song song với đường thẳng d có hệ số 
góc k thì cần phải kiểm tra điều kiện song song. 
Câu 1: Đường cong trong hình bên là đồ 
thị của một hàm số trong bốn hàm số được 
liệt kê ở bốn phương án A, B, C, D dưới 
đây. Hỏi hàm số đó là hàm số nào? 
2 1A. y x x= − + − 3 B. 3 1y x x= − + +
4 2 1y x x= − 3 3 1
C. + D. y x x= − +
(
Nhận xét ⇒ D 
Câu 2: Cho hàm số )y f x= có lim ( ) 1
x
f x→+∞ = và . Khẳng 
định nào sau đây là khẳng định đúng? 
lim ( ) 1
x
f x→−∞ = −
GV: Phạm Bắc Tiến−0995095121 6 Ôn thi TN THPT QG 2017 Ôn thi TN THPT QG 2017 27 GV: Phạm Bắc Tiến−0939319183 
Chương II: THỂ TÍCH KHỐI TRÒN XOAY 
. HÌNH NÓN, KHỐI NÓN: 
A. Đồ thị hàm số đã cho không có tiệm cận ngang. 
B. Đồ thị hàm số đã cho có đúng một tiệm cận ngang. 
1 I và C. Đồ thị hàm số đã cho có hai tiệm cận ngang là y = 1y = −
1
. 
D. Đồ thị hàm số đã cho có hai tiệm cận ngang là x = và 1x = −
42
. 
Nắm lí thuyết ⇒ C 
Câu 3: Hỏi hàm số 1y x= + đồng biến trên khoảng nào? 
A. 1;⎛ ⎞−∞ −⎜ ⎟⎝ ⎠2 (0 B. ; )+∞ C. 
1 ;
2
⎛ ⎞− +∞⎜ ⎟⎝ ⎠ ( ; D. 0)−∞
(y f
Nhận xét ⇒ B 
Câu 4: Cho hàm số )x= xác định, liên 
tục trên \ và có bảng biến thiên. Khẳng 
định nào sau đây là khẳng định đúng? 
A. Hàm số có đúng một cực trị 
B. Hàm số có giá trị cực tiểu bằng 1. 
C. Hàm số có giá trị lớn nhất bằng 0 và giá 
trị nhỏ nhất bằng – 1. 
D. Hàm số đạt cực đại tại 0x = và đạt cực tiểu tại 1x = . 
BBT ⇒ D 
Câu 5: Tìm giá trị cực đại CĐy của hàm số 3 3 2y x x= − +
4= CĐy
. 
A. B. CĐy 1= C. D. 0CĐy = 1CĐy = − 
Nhận xét ⇒ yCĐ = y(−1) ⇒ A 
Câu 6: Tìm giá trị nhỏ nhất của hàm số 
2x
x
3
1
y += − trên đoạn [ ]2;4
6=
4
n y
A. B. [ ]2;4min y [ ]2;mi 2= − C. D. [ ]2;4mi [ ]n 3y = − 2;4
19min
3
y = 
Sử dụng MTCT ⇒ A 
Câu 7: Biết rằng đường thẳng 22y x= − 3 2y x x+ cắt đồ thị (C): = + +
0
tại điểm duy nhất; kí hiệu )0( ;x y 0 là tọa độ của điểm đó. Tìm y 
A. B. C. D. 0y = 4 0y = 0y = 0 1y0 2 = −
mx +
Nhận xét ⇒ C 
Câu 8: Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của 
hàm số 4 2 1 có ba điểm cực trị tạo thành một tam giác 
vuông cân. 
2y x= +
A. 
3 9
m1m = − B. 1= − C. 
3
1
9
m = 1m D. = 
1/ Hình nón: Cho ΔSOA vuông tại 
 A, nOSA= α. Khi cho ΔOSA quay 
quanh cạnh SO thì đường gấp khúc 
OAS tạo thành một hình gọi là hình 
nón. 
 y Hình tròn tâm O gọi là đáy của 
hình nón, bán kính đáy R=OA. 
 ọi là đỉnh, O gọi là tâm củy S g a đáy hình nón. 
 y SO gọi là trục của hình nón. Độ dài đoạn SO gọi là chiều cao. 
 y SA gọi là đường sinh 
 y nBSA = 2α gọi là góc ở đỉnh của hình nón 
2/ Kh i hạn bởi 1 hình nón, kể cả hình nón đó. ối nón: là phần không gian giớ
 Nếu cắt khối nón bởi 1 mặt phẳng chứa trục của khối nón hoặc cắt khối 
nón theo 2 đường sinh thì ta được thiết diện là 1 tam giác cân. 
3/ Diện tích, thể tích của khối trụ: 
 y S = xq 1 chuviđáy.đườ2 ngsinh = πRl; y Stp = Sxq + Sđáy 
 V=y 1 πR2h. 
3
II. HÌNH TRỤ, KHỐI TRỤ: 
1/ Hình trụ Cho hình chữ nhật OO’AB. Quay hình chữ nhậ O: t O’AB quanh 
c nh OO’ thì đường gấp khúc OBAO’ tạo thành 1 hình gọi là ạ hình trụ. 
 y H hình tròai n có tâm O và O’ gọi là 2 đáy. 
 y ọi là OO’ g trục của hình trụ. Độ dài đoạn OO’ gọi là chiều cao. 
 y AB gọi là đường sinh. 
2/ Khối trụ: là phần không gian giới 
hạn bởi 1 hình trụ, kể cả hình trụ đó. 
 Nếu cắt khối trụ bởi 1 mặt phẳng 
song song với trục hoặc chứa trục của 
hình trụ ta được thiết diện là 1 hình chữ 
nhật. 
3/ Diện tích, thể tích của khối trụ: 
 y Sxq = Chuviđáy.đường sinh = 2πRl = 2πRh; y Stp = Sxq + 2Sđáy 
 y V = diệntíchđáy.chiềucao = πR2h. 
α
S 
O A
S 
O AB
OO
O B
A
BO
A
GV: Phạm Bắc Tiến−0995095121 26 Ôn thi TN THPT QG 2017 
A
H
D
S
K
C
B
A. 2
3
h a= . B 4
3
h a= C. 8
3
= D. h a 3
4
h a= 
VS.ABCD = 
1
3
SH.(a 2 )2 = 4 3 SH 2a
3
a ⇒ = 
⇒ HK =
2 2 2
2
22 .. 2
2(2 )
2
aaSH HD
SH D aa
=
⎛ ⎞+ ⎜ ⎟
H+
⎝ ⎠
= 2
3
a ⇒ d(B, (SCD)) = h = 2HK = 4 a 
3
⇒ B 
Ôn thi TN THPT QG 2017 7 GV: Phạm Bắc Tiến−0939319183 
Nhận xét loại trừ, thử sai ⇒ B 
Câu 9: Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của 
hàm số 
2 1
y
mx
1x +
+ có hai tiệm cận ngang. =
A. Không có giá trị thực nào của m thỏa mãn yêu cầu đề bài. 
m mB. C. 0
6=
3x =
2x =
4x =
m
Nhận xét ⇒ D 
Câu 10: Cho một tấm nhôm hình vuông cạnh 12cm. Người ta cắt ở 
bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông 
có cạnh bằng x (cm), rồi gập tấm nhôm lại như hình vẽ dưới đây để 
được một cái hộp không nắp. Tìm x để hộp nhận được có thể tích lớn 
nhất. 
xA. 
B. 
C. 
D. 
Nhận xét kết quả ⇒ C 
Câu 11: Tìm tất cả các giá trị thực của tham số m sao cho hàm số 
tan 2x
tan
y
x m
−= − đồng biến trên khoảng 0; 4
π⎛ ⎞ . ⎜ ⎟⎝ ⎠
0m ≤ 1 2mA. hoặc < 0m B. ≤ C. 1 2m < 2m ≥ D. ≤ ≤
tan 2
tan
ty 2x
x m t m
− −= =− − , t∈(0;1), y’ = 2( )
2 m
x m
−
−
2 0
(0;1)
m
m x
⎧⎨ ≠ ∈⎩>0→ ⇒ A 
− >
GV: Phạm Bắc Tiến−0995095121 8 Ôn thi TN THPT QG 2017 Ôn thi TN THPT QG 2017 25 GV: Phạm Bắc Tiến−0939319183 
Vấn đề 3: Tỉ số thể tích PHẦN II: HÀM SỐ MŨ, HÀM SỐ LOGARIT 
Cho hình chóp S.ABC. Trên các các đường thẳng SA, SB, SC I. KIẾN THỨC CƠ BẢN VỀ LŨY THỪA 
lần lượt lấy các điểm A’, B’, C’ khác S. Khi đó ta có: 1. Các định nghĩa: 
. ' ' '
.
' ' '. .S A B C
S ABC
SA SB SC
V SA SB SC
= V • a (n∈N*, a∈R); • a1 = a ∀a; • a0 = 1 ∀a≠0 Nn
n
a a=
 thua so
. ...a S 
A C 
A B
S
 • 1na
na− = (n∈N*, a ≠ 0); 
 • 
m
nna = ma ( a>0; m∈Z, n∈N*) 
2. Các tính chất : 
TC1: Cho 0< a ≠ 1 và x, y∈R Khi đó: 
 • ax = ay ⇔ x = y 
 • Nếu a > 1 thì ax > ay ⇔ x > y 
 • Nếu 0 ay ⇔ x < y 
Nhận xét: • 
x y
x y
a a
⎧⎨⎩
>
> ⇒ a > 1; • x y
x y
a a
⎩
⇒ 0 < a < 1 
TC2: Cho 0<a<b và x∈R. Khi đó: 
 • ax > bx ⇔ x 0 
TC2: Cho a, b > và x, y∈R. Ta có: 
 • ax.ay = ax + y; • x x yy aa
−=a ; • (ax)y = axy 
 • ax.bx = (a.b)x; • 
xx
x
a a
b b
⎛ ⎞= ⎜⎝ ⎠⎟ 
 Chú ý: 
x xa b
b a
−⎛ ⎞ =⎜ ⎟⎝ ⎠
⎛ ⎞⎜ ⎟⎝ ⎠ 
3. Công thức lãi kép: 
Thể thức lãi kép: gửi tiền vào ngân hàng, nếu đến kì hạn người gửi 
không rút lãi ra thì tiền lãi được cộng vào vốn của kì kế tiếp. Nếu một 
người gửi số tiền A với lãi suất r thì dễ thấy sau n kì số tiền người ấy 
thu được cả vốn lẫn lãi là: C = A(1 + r)n 
 Chú ý: Cho ΔSAB vuông 
tại A, đường cao AH. Ta có: 
SA2 = SH.SB 
⇒ SH = 2SA
SB
 ⇒ 22SH SASB SB= 
Câu 35: Tính thể tích của khối lập phương ABCD.A’B’C’D’, biết 
B 
A’ 
C’ 
H
B’ 
V
' 3AC a= 
A. 3V a B. 
33 6aV = 
4
C. 33 3V a= D. = 31
3
V a= 
nh.AC’ = cạ 3 = a 3 ⇒ c nh = a ⇒ V = a3 ⇒ A 
C ứ giác S.ABCD có đáy ABCD là hình vuông 
ạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và 
ạ
Câu 36: ho hình chóp t
c 2SA a= . Tính 
A. 
thể tích V của khối chóp S.ABCD 
3a2V = B. 
32
4
aV = C. 
6
32V a= D. 
32
3
aV = 
V = 1 SA.a2 = 
3a2 ⇒ D 
3 3
Câu 37: Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông 
góc với nhau; 6 , 7AB a AC a= = và 4AD a= . Gọi M, N ứng là 
trung điểm các cạnh BC, CD, DB. 
, P tương
Tính thể tích V của tứ diện AMNP. 
A. 37
2
V a= 314V a= CB. . 328
3
V a= D. 37a 
P 
 V =
SΔMN =
1 ⇒ V =
4
SΔBCD A.MNP 
1
4
VABCD =
1
4
. 1
6
AB.AC.AD ⇒ D 
Câu 38: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 
bằng 2a , ΔSAD cân tại S và (SAD) ⊥ (ABCD), thể tích khối chóp 
S.ABCD bằng 34
3
a . Tính khoảng cách h từ B đến mp(SCD). 
GV: Phạm Bắc Tiến−0995095121 24 Ôn thi TN THPT QG 2017 
Loại 3: Hình chóp đều 
⇒ Chiều cao = Độ dài đoạn nối đỉnh và tâm của đáy 
1/ Hình chóp tam giác đều: 
V = 1
3
SO.SΔABC=
1
3
SO.
2( ) 3canh
4
y AM = 3 ; 
2
canh
y AO = 3canh
3
= Rngoạitiếpđáy 
y OM = 3 = R pđáy 6
canh
nộitiế
y Sxq = 3 3.SΔSBC = 12 SM.BC; y Stp = Sxq +Sđáy 
y Tứ diệ ó tất cả các cạn đều c nh bằng nhau có thể tích:V=
3( ) 2
12
canh 
y Bán kín ầu ngo p hình chóp là: R = h mặt c ại tiế
2SA
SO
2
2/ Hình c tứhóp giác đều: 
V= 1 SO.(cạnhđ 2 
3
áy)
y Hình chóp tứ giác đều có tất cả 
các cạnh bằng nhau có: 
h = 2canh = R
2 ngoạitiếphìnhchóp 
y Sxq = 3SΔSBC = 4. 12 SM.BC; 
y Stp = Sxq +Sđáy 
y Bán kính mặt cầu ngoại tiếp hình chóp là: R = 
2
2
SA
SO
S
O
A C
B
M
n( , )matben day 
n( , )canhben day 
M
A 
S
B C
D
O
n( , )canhben day
n( , )matben day
Ôn thi TN THPT QG 2017 9 GV: Phạm Bắc Tiến−0939319183 
CÁC DẠNG TOÁN LÃI KÉP: 
PROBLEM 1: Gửi vào a đồng, lãi r/tháng (lãi tháng trước cộng lãi 
tháng sau - lãi kép). Tính số tiền có được sau n tháng (cuối tháng 
thứ n). 
Ví dụ 1: Một người gửi 1 triệu (lãi kép), lãi suất là 0,65%/tháng. Tính 
số tiền có được sau 2 năm? 
 Giải: Áp dụng CT, số tiền là: 1000000.(1 + 0,0065)24 = 1168236,313 
Làm tròn thành: 1168236 (không phải bài nào cũng làm tròn như vậy, 
cần lưu ý). 
Ví dụ 2: Theo thể thức lãi kép, một người gửi 10 triệu đồng vào ngân 
hàng. 
a/ Nếu theo kì hạn 1 năm với lãi suất 7,56% một năm thì sau 2 năm 
người đó thu được một số tiền là: 
 10.(1 + 0,0756)2 ≈ 11,569 triệu đồng 
b/ Nếu theo kì hạn 3 tháng với lãi suất 1,65% một quí thì sau 2 năm 
người đó thu được một số tiền là: 
 10.(1 + 0,0165)8 ≈ 11,399 triệu đồng 
Ví dụ 3: Một người đầu tư 100 triệu đồng vào một công ti theo thể 
thức lãi kép với lãi suất 13% một năm. Hỏi sau 5 năm mới rút lãi thì 
người đó thu được bao nhiêu tiền lãi? (Giả sử lãi suất hàng năm không 
đổi) 
Giải 
Sau 5 năm số tiền lãi người đó thu được là: 
 100.(1 + 0,13)5 − 100 ≈ 84,244 triệu đồng 
PROBLEM 2: Mỗi tháng gửi a đồng (lãi kép - tháng nào cũng gửi 
thêm vào đầu mỗi tháng), lãi r/tháng. Tính sô tiền thu được sau n 
tháng. 
Cuối tháng 1 có số tiền là: a(1+r) 
Cuối tháng 2: [a(1+r)+a](1+r) = a(1+r)2 + a(1+r) 
(đầu tháng 2 gửi thêm a đồng, số tiền cuối tháng 2 được tính bằng số 
tiền đầu tháng 2 + lãi) 
Cu