Ôn tập Hình 11 - Phần 1: Các phép biến hình

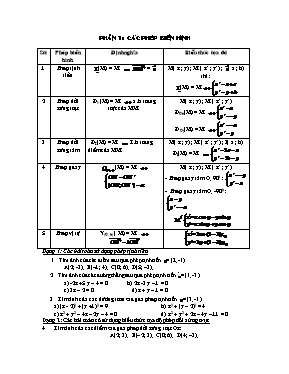
PHẦN 1 : CÁC PHÉP BIẾN HÌNH
Stt
Phép biến hình
Định nghĩa
Biểu thức tọa độ
1
Phép tịnh tiến
(M) = M’ = 
M( x ; y) ; M’( x’ ; y’) ; ( a ; b) thì :
(M) = M’
2
Phép đối xứng trục
Đa (M) = M’ a là trung trực của MM’
M( x ; y) ; M’( x’ ; y’)
ĐOx(M) = M’ 
ĐOy(M) = M’ 
3
Phép đối xứng tâm
 ĐI (M) = M’ I là trung điểm của MM’
M( x ; y) ; M’( x’ ; y’) ; I( a ; b)
ĐI(M) = M’ 
4
Phép quay
(M) = M’ 
M( x ; y) ; M’( x’ ; y’) 
- Phép quay tâm O, 900 : 
- Phép quay tâm O, -900 : 
5
Phép vị tự
V(O, k) ( M) = M’ 
Dạng 1: Các bài tốn sử dụng phép tịnh tiến
Tìm ảnh của các điểm sau qua phép tịnh tiến = (2;-1 )
 A(2; -3), B(–1; 4), C(0; 6), D(5; –3).
Tìm ảnh của cácđường thẳng sau qua phép tịnh tiến = (1;-3 )
 a) -2x +5 y – 4 = 0	b) 2x -3 y – 1 = 0
 c) 3x – 2 = 0	 d) x + y – 1 = 0 
 Tìm ảnh của các đường tròn sau qua phép tịnh tiến = (3;-1 )
	a) (x - 2)2 + (y +1)2 = 9	b) x2 + (y – 2)2 = 4
	c) x2 + y2 – 4x – 2y – 4 = 0	d) x2 + y2 + 2x – 4y – 11 = 0
Dạng 2: Các bài tốn cĩ sử dụng biểu thức tọa độ phép đối xứng trục
Tìm ảnh của các điểm sau qua phép đối xứng trục Ox: 
	A(2; 3), B(–2; 3), C(0; 6), D(4; –3).
Tìm ảnh của các điểm sau qua phép đối xứng trục Oy: 
	A(2; 3), B(–2; 3), C(0; 6), D(4; –3).
Tìm ảnh của điểm A(3; 2) qua phép đối xứng trục d với d: x – y = 0.
Tìm ảnh của các đường thẳng sau qua phép đối xứng trục Ox:
	a) 2x + y – 4 = 0	b) x + y – 1 = 0
Tìm ảnh của các đường thẳng sau qua phép đối xứng trục Oy:
	a) x – 2 = 0	b) x + y – 1 = 0
Tìm ảnh của các đường tròn sau qua phép đối xứng trục Ox:
	a) (x + 1)2 + (y – 1)2 = 9	b) x2 + (y – 2)2 = 4
	c) x2 + y2 – 4x – 2y – 4 = 0	d) x2 + y2 + 2x – 4y – 11 = 0
Tìm ảnh của các đường tròn sau qua phép đối xứng trục Oy:
	a) (x + 1)2 + (y – 1)2 = 9	b) x2 + (y – 2)2 = 4
	c) x2 + y2 – 4x – 2y – 4 = 0	d) x2 + y2 + 2x – 4y – 11 =0
Dạng 3: Tìm ảnh của Điểm, đường thẳng, đường trịn qua phép đối xứng tâm.
Tìm ảnh của các điểm A(2; 3), B(–2; 3), C(0; 6), D(4; –3) qua phép đối xứng tâm 
	a) Tâm O(0; 0)	b) Tâm I(1; –2)	c) Tâm H(–2; 3)
Tìm ảnh của các đường thẳng sau qua phép đối xứng tâm O(0; 0):
	a) 2x – y = 0	b) x + y + 2 = 0	c) 2x + y – 4 = 0 d) y = 2 e) x = –1
Tìm ảnh của các đường thẳng sau qua phép đối xứng tâm I(2; 1):
	a) 2x – y = 0	b) x + y + 2 = 0	c) 2x + y – 4 = 0	d) y = 2 e) x = –1
Tìm ảnh của các đường tròn sau qua phép đối xứng tâm I(2; 1):
	a) (x + 1)2 + (y – 1)2 = 9	b) x2 + (y – 2)2 = 4
	c) x2 + y2 – 4x – 2y – 4 = 0	d) x2 + y2 + 2x – 4y – 11 = 0
Dạng 4:Các bài tốn sử dụng phép quay
 1 Tìm ảnh của các điểm sau qua phép quay Q(O;90);Q(O;-90)
 A(2; -3), B(–1; 4), C(0; 6), D(5; –3).
2 Tìm ảnh của cácđường thẳng sau qua phép quay Q(O;90);Q(O;-90)
 a) -2x +3 y – 7 = 0	b) 2x -5 y – 4 = 0
 c) x – 2 = 0	 d) x - y – 1 = 0 
 3 Tìm ảnh của các đường tròn sau qua phép Q(O;90);Q(O;-90)
	a) (x - 2)2 + (y +1)2 = 9	b) x2 + (y – 2)2 = 4
	c) x2 + y2 – 6x – 2y +6 = 0	d) x2 + y2 + 2x – 4y – 11 = 0
 Dạng 5 :Các bài tốn sử dụng phép vị tự
 1 Tìm ảnh của các điểm sau qua phép vị tự V(I;k) ;I(-3;4);k=-3
 A(2; -3), B(–1; 4), C(0; 6), D(5; –3).
2 Tìm ảnh của cácđường thẳng sau qua phép vị tự V(I;k) ;I(1;-2);k=-5
 a) -2x +3 y – 7 = 0	b) 2x -5 y – 4 = 0
 c) x – 2 = 0	 d) x - y – 1 = 0
 3 Tìm ảnh của các đường tròn sau qua phép vị tự V(I;k) ;I(3;-2);k=-3
	a) (x - 2)2 + (y +1)2 = 9	b) x2 + (y – 2)2 = 4
	c) x2 + y2 – 6x – 2y +6 = 0	d) x2 + y2 + 2x – 4y – 11 = 0