Nguyên hàm – Tích phân - Ứng dụng tích phân- 12 (Phần 3: Ứng dụng Tích phân)

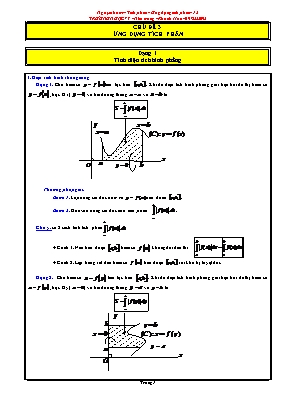
CHỦ ĐỀ 3
 ỨNG DỤNG TÍCH PHÂN
Dạng 1
 Tớnh diện tớch hỡnh phẳng
1. Diện tớch hỡnh thang cong
Dạng 1: Cho hàm số liờn tục trờn . Khi đú diện tớch hỡnh phẳng giới hạn bởi đồ thị hàm số , trục Ox () và hai đường thẳng và là: 
	Phương phỏp giải:
 	Bước 1. Lập bảng xột dấu hàm số trờn đoạn .
 	Bước 2. Dựa vào bảng xột dấu tớnh tớch phõn : .
	Chỳ ý: cú 2 cỏch tớnh tớch phõn 
	+ Cỏch 1: Nếu trờn đoạn hàm số khụng đổi dấu thỡ: 
	+ Cỏch 2: Lập bảng xột dấu hàm số trờn đoạn rồi khử trị tuyệt đối.
	Dạng 2: Cho hàm số liờn tục trờn . Khi đú diện tớch hỡnh phẳng giới hạn bởi đồ thị hàm số , trục Oy () và hai đường thẳng và là: 
2. Diện tớch hỡnh phẳng
	Dạng 1: Cho 2 hàm số và liờn tục trờn . Khi đú diện tớch của hỡnh phẳng (H) giới hạn bởi đồ thị hai hàm số và và hai đường thẳng và là: 
	Phương phỏp giải:
	Bước 1. Lập bảng xột dấu hàm số trờn đoạn .
	Bước 2. Dựa vào bảng xột dấu tớnh tớch phõn .
	Dạng 2: Cho hai hàm số và liờn tục trờn . Diện tớch hỡnh phẳng giới hạn bởi cỏc đường và là: . 
	Trong đú là nghiệm nhỏ nhất và lớn nhất của phương trỡnh 
	Phương phỏp giải:
	Bước 1. Giải phương trỡnh . Giả sử ta tỡm được là nghiệm nhỏ nhất và lớn nhất của phương trỡnh .
	Bước 2. Lập bảng xột dấu hàm số : trờn đoạn .
	Bước 3. Dựa vào bảng xột dấu tớnh tớch phõn: .
	Dạng 3: Cho hai hàm số và liờn tục trờn . Khi đú diện tớch của hỡnh phẳng (H) giới hạn bởi đồ thị hai hàm số và và hai đường thẳng và là: 
	Phương phỏp giải:
	Bước 1. Lập bảng xột dấu hàm số trờn đoạn .
	Bước 2. Dựa vào bảng xột dấu tớnh tớch phõn .
	Dạng 4: Cho hai hàm số và liờn tục trờn . Diện tớch hỡnh phẳng giới hạn bởi cỏc đường và là: . 
Trong đú là nghiệm nhỏ nhất và lớn nhất của phương trỡnh 
	Phương phỏp giải:
	Bước 1. Giải phương trỡnh . Giả sử ta tỡm được là nghiệm nhỏ nhất và lớn nhất của phương trỡnh .
	Bước 2. Lập bảng xột dấu hàm số : trờn đoạn .
	Bước 3. Dựa vào bảng xột dấu tớnh tớch phõn: .
	Dạng 5: khi tớnh diện tớch giới hạn 3 hàm số trở lờn thỡ phương phỏp chung là vẽ đồ thị rồi dựa vào đồ thị để tớnh.
	Cỏch tớnh giới hạn của 3 hàm số: Cho 3 hàm số , và liờn tục trờn . Khi đú diện tớch của hỡnh phẳng (H) giới hạn bởi đồ thị 3 hàm số , và là:
Với: 	+ là nghiệm phương trỡnh: 
	+ là nghiệm phương trỡnh: 
	+ là nghiệm phương trỡnh: 
	Trong đú: 
Túm lại khi giải toỏn ta thường gặp cỏc dạng sau:
	1. Diợ̀n tích S của miờ̀n giới hạn: 
	2. Diợ̀n tích S của miờ̀n giới hạn: 
	3. Diợ̀n tích S của miờ̀n giới hạn: 
Tớnh diện tớch hỡnh phẳng giới hạn bởi cỏc đường: 
	a) 	 	b) 
	c) , trục Ox.	d) 	
	e) 	f) 
	g) 	h) 
	i), , trục Ox.	j) ,
Tớnh diện tớch hỡnh phẳng giới hạn bởi cỏc đường: 
	a) 	b) , trục hoành.
c) 	d) 
	e) , 	trục Ox.	f) 
g) 	; trục Ox.	h) 
	i) 	j) 
Tớnh diện tớch hỡnh phẳng giới hạn bởi cỏc đường: 
	a) , trục Ox.	b) , trục hoành.	
	c) 	d) 	
	e) 	f) 
	g) 	h) 	
Tớnh diện tớch hỡnh phẳng giới hạn bởi cỏc đường: 
a) 	b) 	
c) 	d) 	
e) 	f) 
g) 	h) 
Tớnh diện tớch hỡnh phẳng giới hạn bởi cỏc đường: 
	a) 	b) 	
 c) 	d) 
	e)	f) 
Tớnh diện tớch hỡnh phẳng giới hạn bởi cỏc đường: 
a) 	b) 	
c) , trục Ox.	d) 
e) , trục Ox.	f) , trục hoành.	
Tớnh diện tớch hỡnh phẳng giới hạn bởi cỏc đường: 
a) , trục hoành.	b) 	
c) 	d) 
e)	f) 
g) 	h) 
i) 	k) 
Tớnh diện tớch hỡnh phẳng giới hạn bởi cỏc đường: 
	a) 	b) 	
	c) 	d) 
	e) 	f) 
Tớnh diện tớch hỡnh phẳng giới hạn bởi cỏc đường: 
a) 	b) 	
c) 	d) 	
e)	f) 
g) 	h) 	
Tớnh diện tớch cỏc elip sau:
	a) 	b) 	c) 	d) 
Tớnh diện tớch hỡnh phẳng giới hạn bởi cỏc đường sau:
	a) , và tiờ́p tuyờ́n với (C) tại A(0; 1).	
	b) , và tiờ́p tuyờ́n với (C) tại A(-2; 1).
	c) và hai tiờ́p tuyờ́n với (P) tại A(1;2) và B(4;5).
d) , trục Ox và tiờ́p tuyờ́n của (C ) vẽ từ O.
Tớnh diện tớch hỡnh phẳng giới hạn bởi cỏc đường: 
a) và tiờ́p tuyờ́n với (C) tại điểm cú hoành độ x = 2.
b) và tiờ́p tuyờ́n với (C) tại điểm cú hoành độ x = –2.
c) và tiờ́p tuyờ́n với (C) tại điểm O(0 ; 0) và tại A(3; 3) trờn (C).
d) , và tiờ́p tuyờ́n với (C) tại điểm M thuộc đồ thị cú hoành độọ x = .
e) , tiệm cận xiờn của (C), x = 1 và x = 3.	
f) , tiệm cận xiờn của (C), x = –1 và ứ x = 2
Dạng 2
 Tớnh thể tớch vật thể trũn xoay
x
y
O
f(x)
f(x)
b
a
y
x
c
d
O
 Quay quanh trục Ox	 Quay quanh trục Oy
	Dạng 1: Thể tớch của vật thể trũn xoay khi cho hỡnh phẳng giới hạn bởi cỏc đường , trục Ox và hai đường thẳng và quay xung quanh trục Ox là: . 
	Chỳ ý: Hàm số và liờn tục trờn đoạn .
	Dạng 2: Thể tớch của vật thể trũn xoay khi cho hỡnh phẳng giới hạn bởi cỏc đường , trục Oy và hai đường thẳng và quay xung quanh trục Oy là: . 
	Chỳ ý: Hàm số và liờn tục trờn đoạn .
	Dạng 3: Cho hai hàm số và liờn tục, cựng dấu trờn đoạn . Hỡnh phẳng giới hạn bởi đồ thị của cỏc hàm số trờn và hai đường thẳng và quay xung quanh trục Ox tạo nờn một khối trũn xoay cú thể tớch là: 
	Dạng 4: Cho hai hàm số và liờn tục, cựng dấu trờn đoạn . Hỡnh phẳng giới hạn bởi đồ thị của cỏc hàm số trờn và hai đường thẳng và quay xung quanh trục Ox tạo nờn một khối trũn xoay cú thể tớch là: 
Túm lại khi giải toỏn ta thường gặp cỏc dạng sau:
	1. Thể tớch của khối trũn xoay sinh ra khi quay miờ̀n giới hạn cỏc đường sau:quanh Ox mụ̣t vòng là : .
	2. Thể tớch của khối trũn xoay sinh ra khi quay miờ̀n giới hạn cỏc đường sau:quanh Ox mụ̣t vòng là : .
	3. Thể tớch của khối trũn xoay sinh ra khi quay miờ̀n giới hạn cỏc đường sau:quanh Oy mụ̣t vòng là : .
	4. Thể tớch của khối trũn xoay sinh ra khi quay miờ̀n giới hạn cỏc đường sau:quanh Oy mụ̣t vòng là : .
Tớnh thể tớch hỡnh khối sinh ra bởi hỡnh phẳng (H) giới hạn bởi cỏc đường sau quay quanh trục Ox:
	a) , trục Ox.	 	b) , trục Ox.	
	c) 	d) , trục hoành.
	e) , trục hoành. 	f) , trục Ox.	 
	g) 	h) 
Tớnh thể tớch hỡnh khối sinh ra bởi hỡnh phẳng (H) giới hạn bởi cỏc đường sau quay quanh trục Ox:
	a) 	b) 
	c)	d) 
Tớnh thể tớch hỡnh khối sinh ra bởi hỡnh phẳng (H) giới hạn bởi cỏc đường sau quay quanh trục Ox:
	a) 	b) 	
	c) 	d) 	
	e) 	f) 
 g) 	h) 
 h) 	h) 
Tớnh thể tớch hỡnh khối sinh ra bởi hỡnh phẳng (H) giới hạn bởi cỏc đường sau quay quanh trục Ox:
	a) 	b) 
	c) 	d) 
	e) 	f) 	
	g)	h) 
Tớnh thể tớch hỡnh khối sinh ra bởi hỡnh phẳng (H) giới hạn bởi cỏc đường sau quay quanh trục Oy:
	a) 	b)	c) 
	d) 	e) 	f) 
Tớnh thể tớch hỡnh khối sinh ra bởi hỡnh phẳng (H) giới hạn bởi cỏc đường sau quay quanh trục Ox ; Oy:
	a) 	b) 	 
	c) 	d) 	
	e) 	f) 
	g) 	h) 	
	i) 	j)