Ngân hàng đề trắc nghiệm môn: Toán lớp: 12 (chương trình không phân ban)

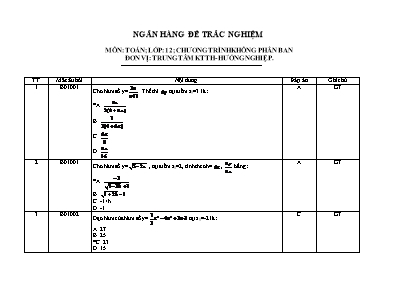
NGÂN HÀNG ĐỀ TRẮC NGHIỆM
MÔN: TOÁN; LỚP: 12; CHƯƠNG TRÌNH KHÔNG PHÂN BAN
ĐƠN VỊ: TRUNG TÂM KTTH- HƯỚNG NGHIỆP.
TT
Mã câu hỏi
Nội dung
Đáp án
Ghi chú
1
B01001
Cho hàm số y=. Thế thì tại điểm x0=3 là:
*A. 
B. 
C. 
D. 
A
GT
2
B01001
Cho hàm số y= , tại điểm x0=2, tính theo h=, bằng:
*A. 
B. 
C. -1+h
D. -1
A
GT
3
B01002
Đạo hàm của hàm số y= tại x0=-2 là:
A. 27
B. 25
*C. 23
D. 15 
C
GT
4
C01001
Đạo hàm của hàm số y= dương khi và chỉ khi:
A. x>0
*B. x1
C. x>1
D. x0
B
GT
5
B01001
Đạo hàm của hàm số y=sinx(1+cosx) là:
A. y'=-cosx-cos2x
B. y'=-cosx-cos2x
*C. y'=cosx+cos2x
D. y'=cosx-cos2x
C
GT
6
B01001
Đạo hàm của hàm số y= là:
A. y'=
B. y'=
C. y'=
*D. y'=
D
GT
7
B01003
Cho hàm số y=. Tìm tất cả giá trị của x để y'=0:
A. 
B. 0,1
C. 
*D. 
D
GT
8
B01003
Đạo hàm của hàm số y= là:
A. y'=
*B. y'=
C. y'=
D. y'=-
B
GT
9
C01003
Đạo hàm của hàm số y=
A. âm khi x>0
*B. âm khi x<0
C. luôn luôn dương
D. luôn luôn âm
B
GT
10
B01003
Đạo hàm cấp n của hàm số y=ln tại x0=-1 bằng:
A. 
B. -1
C. -2
*D. -
D
GT
11
B02001
Khoảng đồng biến của hàm số y=x3-3x2+4 là:
A. (0;2)
*B. 
C. 
D. 
B
GT
12
B02001
Khoảng nghịch biến của hàm số y= là:
*A. 
B. 
C. 
D. 
A
GT
13
B02001
Một khoảng đồng biến của hàm số: là:
A. 
B. 
*C. 
D. 
C
GT
14
B02001
Hàm số: có:
A. một khoảng đồng biến
B. một khoảng đồng biến và một khoảng nghịch biến
C. hai khoảng nghịch biến
*D. hai khoảng đồng biến và một khoảng nghịch biến
D
GT
15
B02001
Tìm số c trong định lý Lagrange áp dụng cho hàm số 
A. 
B. 1
C. 
*D. 2
D
GT
16
C02001
Hàm số nghịch biến trên từng khoảng xác định khi:
A. -1<m<3
*B. -3<m<1
C. 
D. 
B
GT
17
C02001
Tìm tất cả những giá trị của m để hàm số: đồng biến trên khoảng 
A. m1
B. 
*C. 
D. 1<m
C
GT
18
C02001
Có bao nhiêu giá trị nguyên của m để hàm số: nghịch biến trên khoảng (-1;1) ?
A. 8
B. 9
C. 10
*D. 11
D
GT
19
C02001
Có bao nhiêu giá trị nguyên của m để hàm số: 
đồng biến trên từng khoảng xác định ?
*A. vô số
B. 3
C. 4
D. 5
A
GT
20
C02001
Có bao nhiêu giá trị nguyên dương của m để hàm số: 
đồng biến trên khoảng (1;) ?
*A. 0
B. 1
C. 2
D. 3
A
GT
21
B02002
Điểm cực đại của đồ thị hàm số là:
A. -1
*B. 1
C. -2
D. -3 
B
GT
22
B02002
Điểm cực tiểu của đồ thị hàm số là:
A. 0
*B. 
C. 
D. 
B
GT
23
C02002
Hàm số có hai điểm cực trị mà tổng là:
A.-5
*B. -2
C. -1
D. 2
B
GT
24
C02002
Định m để hàm số có ba điểm cực trị
*A. 
B. 
C. 
D. không có
A
GT
25
C02002
Biết đồ thị hàm số có một điểm cực trị thuộc đường thẳng y=x+1, điểm cực trị còn lại là:
*A. 1
B. 2
C. 3
D. 4
A
GT
26
B02003
Giá trị lớn nhất của hàm số là:
A. 1
*B. 2
C. 3
D. 4
B
GT
27
B02003
Giá trị nhỏ nhất của hàm số là:
*A. -27
B. -18
C. -9
D. 0
GT
28
B02004
Khoảng lồi của đồ thị hàm số là:
A. 
B. 
*C. 
D. 
C
GT
29
B02004
Khoảng lõm của đồ thị hàm số là:
A. 
*B. 
C. 
D. 
B
GT
30
C02005
Có bao nhiêu giá trị m để đồ thị hàm số: có đúng hai tiệm cận
A. 0
B. 1
C. 2
*D. mọi m
D
GT
31
C01001
Cho hai điểm A(3;-2) và B(4;3). Hoành độ điểm M trên trục hoành sao cho tam giác MAB vuông tại M là số nào:
A. x=1
*B. x=1 hay x=6
C. x=-2 hay x=3
D. x=1 hay x=2
B
HH
32
C01001
Cho tam giác ABC với A(4;3), B(-5;6) và C(-4;-1). Tọa độ trực tâm H của tam giác là cặp số nào:
A. (3;-2)
B. (-3;-2)
C. (3;2)
*D. (-3;2)
D
HH
33
C01001
Cho tam giác ABC với A(5;5), B(6;-2) và C(-2;4). Tọa độ tâm của đường tròn ngoại tiếp tam giác ABC là cặp số nào:
A. (1;2)
B. (-2;1)
*C. (2;1)
D. (2;2)
C
HH
34
C01001
Cho tam giác ABC có A(1;-1), B(5;-3) và C Oy, trọng tâm G của tam giác ở trên Ox, tọa độ điểm C là:
*A. (0;4)
B. (2;0)
C. (0;-4)
D. (0;2)
A
HH
35
C01002
Cho hình bình hành ABCD, phương trình AB là 3x-y-8=0. Điểm C có tọa độ (6;4). Phương trình đường thẳng CD là:
*A. 3x-y-14=0
B. 3x+y-22=0
C. x+3y-18=0
D. x-3y+6=0
A
HH
36
C01004
Cho đường thẳng d: x-4y+6=0 và : x-y+1=0. Phương trình đường thẳng d', đối xứng của d qua , là: ax+by-1=0. Thế thì a+b=
A. 1
B. 2
*C. 3
D. 4
C
HH
37
C01004
Khi d và d' cắt nhau, giao điểm của d và d' di động trên đường thẳng có phương trình:
A. x+y-1=0
B. x+y+1=0
C. x-y-1=0
*D. x-y+1=0
D
HH
38
C01004
Phương trình đường thẳng đi qua giao điểm của hai đường thẳng d: 3x-2y+1=0;
d': x+3y-2=0 và vuông góc với đường thẳng : 2x+y-1=0 là ax+by+13=0. Thế thì a+b bằng:
A. -12
*B. -11
C. -10
D. -9
B
HH
39
C01005
Khoảng cách từ A(3;1) đến đường thẳng d: gần nhất với số nào dưới đây ?
A. 0,85
*B. 0,14
C. 0,95
D. 1
B
HH
40
C01005
Phương trình đường thẳng song song với đường thẳng d; và cách A(1;1) một khoảng là: x+by+c=0. Thế thì b+c bằng:
*A. 14 hay -16
B. 16 hay -14
C. 10 hay -20
D. 10
A
HH
41
C01005
Cho hình vuông ABCD với AB: 2x+3y-3=0, CD: 2x+3y+10=0. Biết tâm I của hình vuông ở trên trục Ox, hoành độ của nó là:
*A. 
B. 
C. 
D. 
A
HH
42
C01005
Cho tam giác ABC có AB: 2x-y+4=0, AC: x-2y-6=0, B và C Ox. Phương trình phân giác ngoài của góc là:
A. 3x-3y-2=0
B. x-y+10=0
*C. x+y+10=0
D. x+y-1=0
C
HH
43
B01006
Tâm I và bán kính R của đường tròn: là:
A. 
B. 
*C. 
D. 
C
HH
44
C01006
Có bao nhiêu số nguyên m để: là phương trình một đường tròn ?
A. 5
B. 7
*C. 9
D. không có
C
HH
45
C01006
Khi viết phương trình đường tròn tâm I(-3;2) và tiếp xúc với đương thẳng: 2x+y+14=0 dưới dạng , thì P+q+r bằng:
*A. -5
B. -6
C. -8
D. 2
A
HH
46
B01006
Phương trình đường tròn có đường kính AB với A(-3;1), B(5;7) là:
A. 
B. 
*C. 
D. 
C
HH
47
C01006
Phương trình đường tròn có tâm I(6;2) và tiếp xúc ngoài với đường tròn: là:
A. 
B. 
C. 
*D. 
D
HH
48
B01007
Điểm là một tiêu điểm của Elip có phương trình:
A. 
B. 
*C. 
D. 
C
HH
49
B01007
Phương trình chính tắc của elip tâm O, một tiêu điểm là (0;2), một đỉnh là (-1;0)
A. 
*B. 
C. 
D. 
B
HH
50
B01007
Phương trình chính tắc của e lip tâm O, qua hai điểm là:
A. 
B. 
C. 
*D. 
D
HH