Ngân hàng đề thi trắc nghiệm Toán Lớp 12 - Chuyên đề: Tích phân và ứng dụng - Đề số 06

GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM 
CHUYÊN ĐỀ : TÍCH PHÂN VÀ ỨNG DỤNG
ĐỀ SỐ 06
C©u 1 : 
Tìm diện tích hình phẳng giới hạn bởi các đường ; 
A.
B.
C.
ln3
D.
C©u 2 : 
Tìm biết 
A.
B.
C.
D.
C©u 3 : 
Tìm nguyên hàm của hàm số f(x) biết 
A.
B.
Đáp án khác
C.
Tanx-1+C
D.
C©u 4 : 
Tính diện tích hình phẳng giới hạn bởi y=x2-4x+5 và hai tiếp tuyến tại A(1;2) và B(4;5)
A.
94 
B.
74 
C.
34 
D.
54 
C©u 5 : 
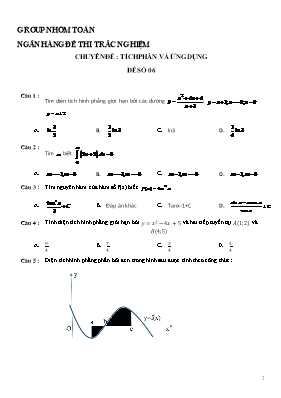
Diện tích hình phẳng phần bôi đen trong hình sau được tính theo công thức:
A.
.
B.
.
C.
.
D.
C©u 6 : 
Tính tích phân 
A.
B.
1
C.
D.
C©u 7 : 
Nếu là một nguyên hàm của và thì là ? 
A.
B.
C.
D.
C©u 8 : 
Diện tích hình phẳng giới hạn bởi và trục Ox là: 
A.
6
B.
C.
D.
C©u 9 : 
Thể tích khối tròn xoay khi quay hình phẳng (H) giới hạn bởi và trục Ox quanh trục Ox là: 
A.
B.
C.
D.
C©u 10 : 
Tính diện tích hình phẳng giới hạn bởi đường cong 
C:y=x2-4x+3 và d:x+3
A.
1096 
B.
1056 
C.
1076 
D.
1036 
C©u 11 : 
Họ nguyên hàm của tanx là:
A.
ln
B.
-ln
C.
D.
ln(cosx) + C
C©u 12 : 
 bằng:
A.
ln
B.
ln
C.
ln
D.
ln
C©u 13 : 
Xét các mệnh đề:
A.
(I) đúng, (II) sai
B.
(I) sai, (II) đúng
C.
Cả (I) và (II) đều đúng
D.
Cả (I) và (II) đều sai
C©u 14 : 
Thể tích khối tròn xoay khi quay hình phẳng (H) giới hạn bởi và quanh trục Ox là: 
A.
B.
C.
D.
C©u 15 : 
Một nguyên hàm của là:
A.
B.
C.
D.
C©u 16 : 
Họ nguyên hàm của hàm số là:
A.
B.
C.
.
D.
C©u 17 : 
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=x3 , trục hoành và các đường thẳng x= -1, x=3 là
A.
(đvdt)
B.
(đvdt)
C.
(đvdt)
D.
(đvdt)
C©u 18 : 
Hàm số nào là nguyên hàm của f(x) = :
A.
F(x) = 
B.
F(x) = 
C.
F(x) = 
D.
C©u 19 : 
Tìm nguyên hàm của hàm số f(x) biết 
A.
B.
Đáp án khác
C.
D.
C©u 20 : 
Nguyên hàm của hàm số là:
A.
B.
C.
D.
C©u 21 : 
Họ nguyên hàm của là:
A.
B.
C.
ln
D.
C©u 22 : 
Diện tích giới hạn bởi đồ thị hàm và đường thẳng 
A.
10
B.
8
C.
6
D.
4
C©u 23 : 
Cho . Giá trị của là:
A.
2
B.
C.
1
D.
C©u 24 : 
Thể tích khối tròn xoay trong không gian Oxyz giới hạn bởi hai mặt phẳng và có thiết diện cắt bởi mặt phẳng vuông góc với Ox tại điểm bất kỳ là đường tròn bán kính là:
A.
 .
B.
 .
C.
 .
D.
 .
C©u 25 : 
Thể tích khối tròn xoay tạo thành khi cho đường x2+(y-1)2=1 quay quanh trục hoành là
A.
(đvtt)
B.
(đvtt)
C.
(đvtt)
D.
(đvtt)
C©u 26 : 
Tính tích phân sau: I=π83π8cotx-tanxdx
A.
ln2 
B.
ln3 
C.
ln2 
D.
ln3 
C©u 27 : 
Cho hàm số hx=sin2x(2+sinx)2. Tìm a,b để hx=acosx(2+sinx)2+bcosx2+sinx và tính I=-π20hxdx
A.
a=-4 và b=2;I=2ln2-2 
B.
a=4 và b=-2; I=ln2-2 
C.
a=2 và b=4;I=2ln2-2 
D.
a=-2 và b=4;I=ln2-2 
C©u 28 : 
Diện tích hình phẳng giới hạn bởi đường thẳng và đường thẳng bằng:
A.
B.
C.
D.
C©u 29 : 
Tính tích phân 
A.
B.
C.
D.
C©u 30 : 
Mệnh đề nào sau đây sai?
A.
Nếu là một nguyên hàm của trên và C là hằng số thì . 
B.
Mọi hàm số liên tục trên đều có nguyên hàm trên . 
C.
 là một nguyên hàm của trên 
D.
C©u 31 : 
A.
B.
C.
1
D.
2
C©u 32 : 
Tìm một nguyên hàm của hàm số biết 
A.
B.
C.
D.
C©u 33 : 
Tính diện tích hình phẳng giới hạn bởi các đường 
C1:fx=e+1x và C2:gx=1+exx
A.
e2-1 
B.
e2-2 
C.
e3-3 
D.
e22-2 
C©u 34 : 
 bằng:
A.
B.
C.
D.
C©u 35 : 
Nguyên hàm của hàm số là:
A.
B.
C.
D.
C©u 36 : 
Gọi là một nguyên hàm của hàm mà . Phát biểu nào sau đây là đúng:
A.
 là hàm chẵn
B.
 là hàm lẻ
C.
 là hàm tuần hoàn chu kỳ 
D.
 không là hàm chẵn cũng không là hàm lẻ
C©u 37 : 
Tính tích phân sau: 
A.
I=4
B.
I=2
C.
I=0
D.
Đáp án khác
C©u 38 : 
Gọi là một nguyên hàm của hàm mà . Giá trị bằng:
A.
B.
 .
C.
.
D.
 .
C©u 39 : 
Cho .Giải phương trình 
A.
B.
C.
D.
C©u 40 : 
Diện tích hình phẳng giới hạn bởi và là: 
A.
B.
C.
D.
C©u 41 : 
Cho hai hàm số là hàm số liên tục ,có lần lượt là nguyên hàm của .Xét các mệnh đề sau :
(I): là một nguyên hàm của 
(II): là một nguyên hàm của 
(III): là một nguyên hàm của 
Mệnh đề nào là mệnh đề đúng ?
A.
I
B.
I và II
C.
I,II,III
D.
II
C©u 42 : 
 bằng
A.
B.
C.
D.
C©u 43 : 
Biết rằng tích phân , tích bằng:
A.
1 
B.
-1
C.
-15
D.
5
C©u 44 : 
Tính tích phân sau: I=02xa-xdx
A.
Cả 3 đáp án trên
B.
2a-83 
C.
13a3+83-2a 
D.
83-2a 
C©u 45 : 
Hàm số nào là nguyên hàm của f(x) = :
A.
F(x) = 1 + cot
B.
F(x) = 
C.
F(x) = ln(1 + sinx)
D.
F(x) = 2tan
C©u 46 : 
Thể tích khối tròn xoay tạo thành khi quay quanh trục hoành hình phẳng giới hạn bởi các đường và y=x2 là
A.
(đvtt)
B.
(đvtt)
C.
(đvtt)
D.
(đvtt)
C©u 47 : 
Tính diện tích hình phẳng giới hạn bởi P:y2=4x và d:y=2x-4
A.
9
B.
3
C.
7
D.
5
C©u 48 : 
Một nguyên hàm của là:
A.
B.
C.
D.
C©u 49 : 
Tìm diện tích hình phẳng giới hạn bởi các đường và 
A.
9
B.
C.
D.
C©u 50 : 
Hàm số là nguyên hàm của hàm số f(x) nào
A.
B.
Đáp án khác
C.
D.
C©u 51 : 
 bằng:
A.
B.
C.
D.
C©u 52 : 
Nếu thì là hàm nào ? 
A.
B.
C.
D.
C©u 53 : 
 bằng:
A.
B.
C.
D.
C©u 54 : 
Họ nguyên hàm của là:
A.
ln
B.
ln
C.
-ln
D.
ln
C©u 55 : 
Họ nguyên hàm của f(x) = sin
A.
B.
C.
D.
C©u 56 : 
Cho . Khi đó bằng:
A.
B.
C.
7
D.
3
C©u 57 : 
Cho hình phẳng (H) giới hạn bởi các đường . TÌm m để diện tích hình phẳng đó bằng 
A.
B.
C.
D.
C©u 58 : 
 bằng:
A.
B.
C.
D.
C©u 59 : 
Tính tích phân sau: I=02x-1dx
A.
1
B.
11
C.
6
D.
3
C©u 60 : 
Cho hàm số Khi đó bằng ?
A.
B.
C.
D.
C©u 61 : 
Diện tích hình phẳng giới hạn bởi đồ thị hàm số và trục hoành bằng:
A.
4
B.
0
C.
2
D.
8
C©u 62 : 
Hàm nào không phải nguyên hàm của hàm số :
A.
B.
C.
D.
C©u 63 : 
Gọi S là diện tích giới hạn bởi đồ thị hàm số ,tiệm cận xiên của đồ thi và các đường thẳng .Tìm giá trị để 
A.
B.
C.
D.
C©u 64 : 
Tìm nguyên hàm của hàm số f(x) biết 
A.
Đáp án khác
B.
C.
D.
C©u 65 : 
Để thì giá trị của là bao nhiêu ?
A.
1
B.
3
C.
2
D.
4
C©u 66 : 
Cho hình phẳng trong hình (phần tô đậm ) quay quanh trục hoành .Thể tích khối tròn xoay tạo thành được tính theo công thức nào ?
A.
B.
C.
D.
C©u 67 : 
Họ nguyên hàm của là:
A.
B.
C.
D.
C©u 68 : 
Đặt .
Nghiệm của phương trình là
A.
B.
C.
D.
C©u 69 : 
Nguyên hàm của hàm số là:
A.
B.
C.
D.
C©u 70 : 
Họ nguyên hàm của là:
A.
B.
C.
D.
C©u 71 : 
Họ nguyên hàm của f(x) = là:
A.
F(x) = ln
B.
F(x) = ln
C.
F(x) = 
D.
F(x) = ln
C©u 72 : 
Tính tích phân sau: I=-π12π12tanx.tanπ3-xtan⁡(π3+x)dx
A.
13ln2 
B.
23ln2 
C.
23ln3 
D.
13ln3 
C©u 73 : 
Một nguyên hàm của f(x) = xelà:
A.
B.
C.
D.
C©u 74 : 
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=x2 và đường thẳng y= - x+2 là
A.
(đvdt)
B.
11 (đvdt)
C.
7 (đvdt)
D.
Một kết quả khác
C©u 75 : 
Tính diện tích hình phẳng được giới hạn bởi đường cong 
C:fx=-3x-1x-1 và hai trục tọa độ.
A.
-1+ln43 
B.
-1+ln7 
C.
-1+2ln2 
D.
-1+ln53 
C©u 76 : 
Tìm nguyên hàm của hàm số f(x) biết 
A.
B.
C.
D.
C©u 77 : 
Cho .Xác định để 
A.
B.
C.
D.
C©u 78 : 
Tích phân . Tổng của bằng:
A.
1.
B.
7
C.
-3
D.
2
C©u 79 : 
Tính bằng:
A.
B.
C.
D.
C©u 80 : 
Tìm công thức sai:
A.
B.
C.
D.
ĐÁP ÁN
01
{ | ) ~
28
) | } ~
55
{ ) } ~
02
{ | ) ~
29
{ | ) ~
56
{ | ) ~
03
{ | } )
30
{ | ) ~
57
{ | } )
04
) | } ~
31
{ | ) ~
58
{ ) } ~
05
) | } ~
32
{ | ) ~
59
) | } ~
06
{ | ) ~
33
) | } ~
60
{ ) } ~
07
{ ) } ~
34
{ | ) ~
61
) | } ~
08
{ | } )
35
{ | } )
62
) | } ~
09
{ | } )
36
) | } ~
63
{ ) } ~
10
) | } ~
37
{ | } )
64
{ | } )
11
{ ) } ~
38
) | } ~
65
{ ) } ~
12
{ ) } ~
39
{ ) } ~
66
{ ) } ~
13
{ | ) ~
40
{ | } )
67
{ | ) ~
14
{ | } )
41
{ ) } ~
68
{ | ) ~
15
{ | ) ~
42
{ | ) ~
69
{ | } )
16
) | } ~
43
) | } ~
70
{ | ) ~
17
{ | } )
44
) | } ~
71
{ ) } ~
18
{ ) } ~
45
{ ) } ~
72
) | } ~
19
{ | } )
46
{ | } )
73
{ ) } ~
20
{ | } )
47
) | } ~
74
{ | } )
21
{ ) } ~
48
{ | ) ~
75
) | } ~
22
{ ) } ~
49
{ | ) ~
76
{ | } )
23
{ | ) ~
50
{ | } )
77
{ ) } ~
24
) | } ~
51
{ | ) ~
78
) | } ~
25
{ | } )
52
{ ) } ~
79
{ | } )
26
) | } ~
53
{ | ) ~
80
{ | } )
27
) | } ~
54
{ ) } ~