Ngân hàng đề thi trắc nghiệm Giải tích 12 - Tích phân va ứng dụng

 1 
GROUP NHÓM TOÁN 
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM 
CHUYÊN ĐỀ : TÍCH PHÂN VÀ ỨNG DỤNG 
ĐỀ SỐ 01 
C©u 1 : 
Hàm số nào dưới đây không là nguyên hàm của hàm số 
2
(2 )
( )
( 1)
x x
f x
x



A. 
2 1
1
x x
x
 

 B. 
2 1
1
x x
x
 

 C. 
2 1
1
x x
x
 

 D. 
2
1
x
x 
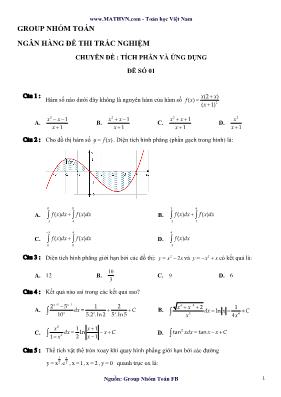
C©u 2 : Cho đồ thị hàm số ( )y f x . Diện tích hình phẳng (phần gạch trong hình) là: 
A. 
0 0
3 4
( ) ( )f x dx f x dx

  B. 
1 4
3 1
( ) ( )f x dx f x dx

  
C. 
3 4
0 0
( ) ( )f x dx f x dx

  D. 
4
3
( )f x dx

 
C©u 3 : Diện tích hình phẳng giới hạn bởi các đồ thị: 2 2y x x  và 2y x x   có kết quả là: 
A. 12
B. 
10
3
 C. 9 D. 6 
C©u 4 : Kết quả nào sai trong các kết quả sao? 
A. 
1 12 5 1 2
10 5.2 .ln2 5 .ln5
x x
x x x
dx C
 
   B. 
4 4
3 4
2 1
ln
4
x x
dx x C
x x
 
   
C. 
2
2
1 1
ln
2 11
x x
dx x C
xx

  

 D. 
2tan tanxdx x x C   
C©u 5 : Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường
    
1 x
2 2
y x .e , x 1, x 2 , y 0 quanh trục ox là: 
www.MATHVN.com - Toán học Việt Nam
Nguồn: Group Nhóm Toán FB
 2 
A. 
2(e )e  B. 2(e )e  C. 2e D. e 
C©u 6 : Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường
   
4
y , y 0 , x 1 , x 4
x
 quanh trục ox là: 
A. 6 B. 4 C. 12 D. 8 
C©u 7 : 
Giá trị của 
4
4
2
0
1
(1 tan ) .
cos
x dx
x

 bằng: 
A. 
1
5
 B. 
1
3
 C. 
1
2
 D. 
1
4
C©u 8 : 
Nếu ( ) 5
d
a
f x dx  ; ( ) 2
d
b
f x dx  , với a d b  thì ( )
b
a
f x dx bằng: 
A. 2 B. 3 C. 8 D. 0 
C©u 9 : 
Hàm số 
2
( ) ln
x
x
e
e
f x t tdt  đạt cực đại tại ?x  
A. ln2 B. 0 C. ln2 D. ln4 
C©u 10 : 
Cho tích phân 
2
2
sin 3
0
.sin cosxI e x xdx

  . Nếu đổi biến số 
2sint x thì 
A. 
1
0
1
(1 )
2
tI e t dt  B. 
1 1
0 0
2 t tI e dt te dt
 
  
 
  
C. 
1
0
2 (1 )tI e t dt  D. 
1 1
0 0
1
2
t tI e dt te dt
 
  
 
  
C©u 11 : Diện tích hình phẳng giới hạn bởi hai đường thẳng x = 0, x  và đồ thị của hai hàm số y = 
cosx, y = sinx là: 
A. 2 2 B. 2 C. 2 D. 2 2 
C©u 12 : Diện tích hình phẳng giới hạn bởi các đường 2y x ,trục Ox và đường thẳng 
x 2 là: 
A. 8 B. 
8
3
 C. 16 D. 
16
3
www.MATHVN.com - Toán học Việt Nam
Nguồn: Group Nhóm Toán FB
 3 
C©u 13 : Cho hình phẳng  H giới hạn bởi các đường y sin x ; x 0 ; y 0 và x   . Thể tích vật thể 
tròn xoay sinh bởi hình  H quay quanh Ox bằng 
A. 2 B. 
2
2

 C. 
2
4

 D. 
2

C©u 14 : 
Cho tích phân 
3 2
2
1
1 x
I dx
x

  . Nếu đổi biến số 
2 1x
t
x

 thì 
A. 
2
3 2
2
2
1
t dt
I
t
 

 B. 
3 2
2
2 1
t dt
I
t


 C. 
2
3
2
2
1
tdt
I
t


 D. 
3
2
2 1
tdt
I
t


C©u 15 : Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2 1y x x  và trục ox và đường thẳng x=1 
là: 
A. 
3 2 2
3

 B. 
3 2 1
3

 C. 
2 2 1
3

 D. 
3 2
3

C©u 16 : 
Tìm nguyên hàm: 3 2
4
( )x dx
x
 
A. 
3 55 4ln
3
x x C  B. 
3 53 4ln
5
x x C   
C. 
3 53 4ln
5
x x C  D. 
3 53 4ln
5
x x C  
C©u 17 : 
Tích phân 2
0
cos sinx xdx

 bằng: 
A. 
2
3
 B. 
2
3
 C. 
3
2
 D. 0 
C©u 18 : 
Hàm số nào sau đây không là nguyên hàm của hàm số 
2
(2 )
( )
( 1)
x x
f x
x



A. 
2 1
1
x x
x
 

 B. 
2 1
1
x x
x
 

 C. 
2
1
x
x 
 D. 
2 1
1
x x
x
 

C©u 19 : Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2 4 5y x x   và hai tiếp tuyến với đồ thị 
hàm số tai A(1;2) và B(4;5) có kết quả dạng 
a
b
 khi đó: a+b bằng 
A. 12 B. 
13
12
 C. 13 D. 
4
5 
www.MATHVN.com - Toán học Việt Nam
Nguồn: Group Nhóm Toán FB
 4 
C©u 20 : 
Giá trị của tích phân  
2
2
1
I x 1 ln xdx  là: 
A. 
2ln 2 6
9

 B. 
6ln 2 2
9

 C. 
2ln 2 6
9

 D. 
6ln 2 2
9

C©u 21 : 
Kết quả của 
21
x
dx
x
 là: 
A. 21 x C  B. 2
1
1
C
x



 C. 
2
1
1
C
x


 D. 21 x C   
C©u 22 : Hàm số ( ) ln sin 3cosF x x x  là một nguyên hàm của hàm số nào trong các hàm số sau 
đây: 
A. 
cos 3sin
( )
sin 3cos
x x
f x
x x



 B. ( ) cos 3sinf x x x  
C. 
cos 3sin
( )
sin 3cos
x x
f x
x x
 


 D. 
sin 3cos
( )
cos 3sin
x x
f x
x x



C©u 23 : 
Giá trị của tích phân 
e 2
1
x 2ln x
I dx
x

  là: 
A. 
2e 1
2

 B. 
2e 1
2

 C. 2e 1 D. 2e 
C©u 24 : 
Giả sử 
4
0
2
I sin 3x sin 2xdx a b
2

   , khi đó, giá trị của a b là: 
A. 
1
6
 B. 
3
10
 C. 
3
10
 D. 
1
5
C©u 25 : 
Tìm nguyên hàm: 2
3
( 2 )x x dx
x
  
A. 
3
343ln
3 3
x
x x C   B. 
3
343ln
3 3
x
X x  
C. 
3
343ln
3 3
x
x x C   D. 
3
343ln
3 3
x
x x C   
C©u 26 : 
Tìm nguyên hàm:
1
( 3)
dx
x x 
www.MATHVN.com - Toán học Việt Nam
Nguồn: Group Nhóm Toán FB
 5 
A. 
2
ln
3 3
x
C
x


 B. 
1
ln
3 3
x
C
x
 

 C. 
1 3
ln
3
x
C
x

 D. 
1
ln
3 3
x
C
x


C©u 27 : Diện tích hình phẳng giới hạn bởi các đường (P): y=2x2 , (C): y= 2x1 và Ox là: 
A. 3 2 2 B. 2 2
2

 C. 
23
28 
 D. 4 2  
C©u 28 : 
Diện tích hình phẳng giới hạn bởi các đồ thị hàm số 
2
2 x 27y=x ; y= ; y=
8 x
 là: 
A. 27ln2-3
B. 
63
8
 C. 27ln2 D. 27ln2+1
C©u 29 : Tìm nguyên hàm: 2(1 sin )x dx 
A. 
2 1
2cos sin 2
3 4
x x x C   ; B. 
2 1
2cos sin 2
3 4
x x x C   ; 
C. 
2 1
2cos 2 sin 2
3 4
x x x C   ; D. 
2 1
2cos sin 2
3 4
x x x C   ; 
C©u 30 : 
Cho 
2
2
1
2 1I x x dx  và 
2 1u x  . Chọn khẳng định sai trong các khẳng định sau: 
A. 
2
1
I udu  B. 
3
0
I udu  C. 
2
27
3
I  D. 
3
3
2
0
2
3
I u 
C©u 31 : 
Cho biết  
5
2
f x dx 3 ,  
5
2
g t dt 9 . Giá trị của    
5
2
A f x g x dx    là: 
A. 
Chưa xác định 
được 
B. 12 C. 3 D. 6 
C©u 32 : Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2y x và đường thẳng 2y x là: 
A. 
4
3
 B. 
3
2
 C. 
5
3
 D. 
23
15
C©u 33 : Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = 2 x - 4x - 62 trục hoành và hai đường 
thẳng x=-2 , x=-4 là 
A. 12 B. 
40
3
 C. 
92
3
 D. 
50
3
www.MATHVN.com - Toán học Việt Nam
Nguồn: Group Nhóm Toán FB
 6 
C©u 34 : 
Giả sử rằng 
0 2
1
3x 5x 1 2
I dx a ln b
x 2 3

 
  

. Khi đó, giá trị của a 2b là: 
A. 30 B. 40 C. 50 D. 60 
C©u 35 : Kết quả của ln xdx là: 
A. lnx x x C  B. Đáp án khác C. lnx x C D. lnx x x C  
C©u 36 : 
Tìm nguyên hàm: 3
5
( )x dx
x
 
A. 
525ln
5
x x C  B. 
525ln
5
x x C   
C. 
525ln
5
x x C   D. 
525ln
5
x x C  
C©u 37 : 
Tìm nguyên hàm: 
1
( 3)
dx
x x 
. 
A. 
1
ln
3 3
x
C
x


 B. 
1 3
ln
3
x
C
x

 C. 
1
ln
3 3
x
C
x


 D. 
1 3
ln
3
x
C
x

 
C©u 38 : Diện tích hình phẳng giới hạn bởi các đường cong 3y x và 5y x bằng: 
A. 4 B. 
1
6
 C. 0 D. 2 
C©u 39 : 
Cho hai tích phân 
2
2
0
sin xdx

 và 
2
2
0
cos xdx

 , hãy chỉ ra khẳng định đúng: 
A. 
2 2
2 2
0 0
sin cosxdx xdx
 
  
B. Không so sánh được
C. 
2 2
2 2
0 0
sin cosxdx xdx
 
  D. 
2 2
2 2
0 0
sin = cosxdx xdx
 
  
C©u 40 : 
Cho hai tích phân 
2
2
0
sinI xdx

  và 
2
2
0
cosJ xdx

  . Hãy chỉ ra khẳng định đúng: 
A. I J B. I J C. I J D. 
Không so sánh 
được 
www.MATHVN.com - Toán học Việt Nam
Nguồn: Group Nhóm Toán FB
 7 
C©u 41 : Hàm số 
2
( ) xF x e là nguyên hàm của hàm số 
A. 
2
( ) 2 xf x xe B. 2( ) xf x e C. 
2
( )
2
xe
f x
x
 D. 
22( ) 1xf x x e  
C©u 42 : 
Tính 
ln 2
2 x dx
x
 , kết quả sai là: 
A.  2 2 1x C  B. 2 x C C. 12 x C  D.  2 2 1x C  
C©u 43 : 
Cho tích phân 
2
0
sin
1 2 cos
x
I
x

 

 
 , với 1  thì I bằng: 
A. 
2

 B. 2 C. 2 D. 
2

C©u 44 : Diện tích hình phẳng giới hạn bởi các đồ thị hàm số 2 1 , 5y x y x    có kết quả là 
A. 
35
12
 B. 
10
3
 C. 
73
3
 D. 
73
6 
C©u 45 : 
Nếu ( ) 5
d
a
f x dx  , ( ) 2
d
b
f x dx  với a < d < b thì ( )
b
a
f x dx bằng 
A. -2
B. 0
C. 8
D. 3 
C©u 46 : Kết quả nào sai trong các kết quả sao? 
A. 
1
tan
1 cos 2 2
dx x
C
x
 

 B. 
2
2 2
1 1 1
ln
21 1 1
dx x
C
x x x
 
 
  
 
C. ln(ln(ln ))
ln .ln(ln )
dx
x C
x x x
  D. 22
1
ln 3 2
43 2
xdx
x C
x
   

C©u 47 : Diện tích hình phẳng giới hạn bởi hai đường cong y = x3 – x và 
y = x – x2 là : 
A. Đáp án khác B. 
37
6
 C. 
33
12
 D. 
37
12
C©u 48 : 
Tìm nguyên hàm: 3
2
( )x x dx
x
  
www.MATHVN.com - Toán học Việt Nam
Nguồn: Group Nhóm Toán FB
 8 
A. 
4 31 22ln
4 3
x x x C   B. 4 3
1 2
2ln
4 3
x x x C   
C. 
4 31 22ln
4 3
x x x C   D. 
4 31 22ln
4 3
x x x C   
C©u 49 : Cho hình phẳng giới hạn bởi các đường y x và y x quay xung quanh trục Ox . Thể tích 
khối tròn xoay tạo thành bằng: 
A.  B. 
6

 C. 0 D.  
C©u 50 : Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường
2x y x   y , y 0 , quanh trục ox là: 
A. 
7
12

 B. 6 C. 
35
12

 D. 
6
5

C©u 51 : 
Biến đổi 
3
0 1 1
x
dx
x 
 thành 
2
1
( )f t dt , với 1t x  . Khi đó ( )f t là hàm nào trong các hàm 
số sau? 
A. 
2( ) 2 2f t t t  B. 2( )f t t t  C. 2( )f t t t  D. 2( ) 2 2f t t t  
C©u 52 : 
Cho 2
0
cosxI e xdx

  ; 
2
0
sinxJ e xdx

  và 
0
cos2xK e xdx

  . Khẳng định nào đúng trong các 
khẳng định sau? 
(I) I J e  
(II) I J K  
(III) 
1
5
e
K
 
 
A. Chỉ (II) B. Chỉ (III) C. Chỉ (I) D. Chỉ (I) và (II) 
C©u 53 : Hàm số 2y tan 2x nhận hàm số nào dưới đây là nguyên hàm? 
A. 2tan 2x x B. 
1
tan 2x x
2
 C. tan 2x x D. 
1
tan 2x x
2
 
C©u 54 : Thể tích vật thể tròn xoang khi quay hình phẳng giới hạn bởi đồ thị hàm số y = x
2 2;x y
quanh trục ox là 
www.MATHVN.com - Toán học Việt Nam
Nguồn: Group Nhóm Toán FB
 9 
A. 
2
10

 B. 
4
3

 C. 
3
10

 D. 
10

C©u 55 : 
Cho 
6
0
1
sin cos
64
nI x xdx

  . Khi đó n bằng: 
A. 3 B. 4 C. 6 D. 5 
C©u 56 : Tìm nguyên hàm: 3 2(2 )xe dx 
A. 
3 64 13
3 6
x xx e e C   B. 3 6
4 5
4
3 6
x xx e e C   
C. 
3 64 14
3 6
x xx e e C   D. 
3 64 14
3 6
x xx e e C   
C©u 57 : 
Giả sử 
5
1
ln
2 1
dx
K
x


. Giá trị của K là: 
A. 3 B. 8 C. 81 D. 9 
C©u 58 : Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x + 11x - 6,
3
 y = 6x2, 0, 2x x có 
kết quả dạng 
a
b
 khi đó a-b bằng 
A. 2 B. -3 C. 3 D. 59 
C©u 59 : Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = -x + 4x2 và các tiếp tuyến với đồ thị 
hàm số biết tiếp tuyến đi qua M(5/2;6) có kết quả dạng 
a
b
 khi đó a-b bằng 
A. 
12
11
 B. 14
C. 5
D. -5
C©u 60 : Diện tích hình phẳng giới hạn bởi (C): y= x2+3x2, d1:y = x1 và d2:y=x+2 có kết quả là
A. 
1
8
 B. 
2
7
 C. 
12
1
 D. 
1
6 
C©u 61 : Diện tích hình phẳng giới hạn bởi đường cong y = x2 + 1, tiếp tuyến với đường này tại điểm 
M(2; 5) và trục Oy là: 
A. 
7
3
 B. 
5
3
 C. 2 D. 
8
3
www.MATHVN.com - Toán học Việt Nam
Nguồn: Group Nhóm Toán FB
 10 
C©u 62 : 
Giá trị của 
1
x
0
I x.e dx  là: 
A. 1 B. 
2
1
e
 C. 
2
e
 D. 2e 1 
C©u 63 : 
Tính 
1
dx
x
 , kết quả là: 
A. 
1
C
x
 B. 2 1 x C   C. 
2
1
C
x


 D. 1C x 
C©u 64 : Diện tích hình phẳng giới hạn bởi các đồ thị hàm số y = ( 1)e x và (1 )xy e x là: 
A. 2
2
e
 B. 2 C. 1
2
e
 D. 
3
1
e
 
C©u 65 : Diện tích hình phẳng giới hạn bởi đồ thị hàm số 22 3y x x    và trục hoành là: 
A. 
125
24
 B. 
125
34
 C. 
125
14
 D. 
125
44
C©u 66 : 
Diện tích hình phẳng giới hạn bởi đường thẳng 4y x  và patabol 
2
2
x
y  bằng: 
A. 
28
3
 B. 
25
3
 C. 
22
3
 D. 
26
3
C©u 67 : Diện tích hình phẳng giới hạn bởi các đồ thị: 2 4 3y x x   và y=x+3 có kết quả là: 
A. 
55
6
 B. 
205
6
 C. 
109
6
 D. 
126
5
C©u 68 : 
Tìm nguyên hàm: 2
3
( 2 )x x dx
x
  
www.MATHVN.com - Toán học Việt Nam
Nguồn: Group Nhóm Toán FB
 11 
A. 
3 1
2sinx sin 2
2 4
x x C   B. 
3 1
2sinx- sin 2
2 4
x x C  
C. 
3 1
2cos x sin 2
2 4
x x C   D. 
3 1
2sinx sin 2
2 4
x x C   
C©u 69 : Diện tích hình phẳng giới hạn bởi các đường cong siny x x  và y x , với 0 2x   
bằng: 
A. 4 B. 4 C. 0 D. 1 
C©u 70 : 
Cho  F x là một nguyên hàm của hàm số 2
1
y
cos x
  và  F 0 1 . Khi đó, ta có  F x là: 
A. tan x B. tan x 1  C. tan x 1 D. tan x 1 
C©u 71 : Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đồ thị hàm số y = 82 x và 
x=2 quanh trục ox là: 
A. 12 B. 4 C. 16 D. 8 
C©u 72 : Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường 21 , 0x y  y quanh 
trục ox có kết quả dạng 
a
b

 khi đó a+b có kết quả là: 
A. 11 B. 17 C. 31 D. 25 
C©u 73 : 
Nguyên hàm ( )F x của hàm số 
2
2 1
( )
x
f x
x
 
  
 
 là hàm số nào trong các hàm số sau? 
A. 
3 1
( ) 2
3
x
F x x C
x
    B. 
3 1
( ) 2
3
x
F x x C
x
    
C. 
3
2
3( )
2
x
x
F x C
x

  D. 
3
3
2
3( )
2
x
x
F x C
x
 
 
  
 
 
 
C©u 74 : Diện tích hình phẳng giới hạn bởi các đường (P): y =x2-2x+2 và các tiếp tuyến bới (P) biết 
tiếp tuyến đi qua A(2;-2) là: 
A. 
8
3
 B. 
64
3
 C. 
16
3
 D. 
40
3
C©u 75 : Thể tích khối tròn xoay tạo nên khi quay quanh trục Ox hình phẳng giới hạn bởi các đường y 
=(1- x)2, y = 0, x = 0 và x = 2 bằng: 
www.MATHVN.com - Toán học Việt Nam
Nguồn: Group Nhóm Toán FB
 12 
A. 2 B. 
8 2
3

 C. 
5
2

 D. 
2
5

C©u 76 : Thể tích khối tròn xoay được tạo bởi phép quay quanh trục Ox hình phẳng giới hạn bởi các 
đường y = x2 và x = y2 bằng: 
A. 10 B. 
10
3

 C. 3 D. 
3
10

C©u 77 : 
Giá trị của 
2
2
0
2 xe dx bằng: 
A. 4 1e  B. 44e C. 4e D. 43e 
C©u 78 : Diện tích hình phẳng giới hạn bởi đồ thị hàm số 3y = - x + 3x + 1 và đường thẳng y=3 là 
A. 
57
4
 B. 
45
4
 C. 
27
4
 D. 
21
4
C©u 79 : Tìm khẳng định sai trong các khẳng định sau: 
A. 
2
0 0
sin 2 sin
2
x
dx xdx


  B. 
1
0
(1 ) 0xx dx  
C. 
1 1
0 0
sin(1 ) sinx dx xdx   D. 
1
2007
1
2
(1 )
2009
x x dx

  
www.MATHVN.com - Toán học Việt Nam
Nguồn: Group Nhóm Toán FB
 13 
ĐÁP ÁN 
01 { ) } ~ 28 { | ) ~ 55 ) | } ~ 
02 ) | } ~ 29 { | } ) 56 { | } ) 
03 { | ) ~ 30 ) | } ~ 57 ) | } ~ 
04 ) | } ~ 31 { ) } ~ 58 { | ) ~ 
05 { | ) ~ 32 ) | } ~ 59 { | ) ~ 
06 { | ) ~ 33 { | ) ~ 60 { | ) ~ 
07 ) | } ~ 34 { ) } ~ 61 { | } ) 
08 { ) } ~ 35 { | } ) 62 { ) } ~ 
09 ) | } ~ 36 { | } ) 63 { ) } ~ 
10 ) | } ~ 37 { | } ) 64 { | ) ~ 
11 { | } ) 38 { ) } ~ 65 ) | } ~ 
12 { ) } ~ 39 { | } ) 66 ) | } ~ 
13 { ) } ~ 40 { ) } ~ 67 { | ) ~ 
14 ) | } ~ 41 ) | } ~ 68 { | } ) 
15 { | ) ~ 42 { ) } ~ 69 { ) } ~ 
16 { | } ) 43 ) | } ~ 70 { ) } ~ 
17 { ) } ~ 44 { | ) ~ 71 { | ) ~ 
18 { | } ) 45 { | } ) 72 { | ) ~ 
19 { | ) ~ 46 ) | } ~ 73 ) | } ~ 
20 { ) } ~ 47 { | } ) 74 { | ) ~ 
21 { | } ) 48 { | } ) 75 { | } ) 
22 ) | } ~ 49 { ) } ~ 76 { | } ) 
23 { ) } ~ 50 { | ) ~ 77 ) | } ~ 
24 { ) } ~ 51 ) | } ~ 78 { | ) ~ 
25 { | } ) 52 ) | } ~ 79 { ) } ~ 
26 { | } ) 53 { ) } ~ 
27 { | ) ~ 54 { | ) ~ 
www.MATHVN.com - Toán học Việt Nam
Nguồn: Group Nhóm Toán FB
 1 
GROUP NHÓM TOÁN 
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM 
CHUYÊN ĐỀ : TÍCH PHÂN VÀ ỨNG DỤNG 
ĐỀ SỐ 02 
C©u 1 : Tính 
 dxex x 1
2
. 
A. 
2 1xe C  B. 
21
2
xe C C. 
2 11
2
xe C  D. 
2 11
2
xe C  3 
C©u 2 : Thể tích của khối tròn xoay tạo thành khi quay hình phẳng D giới hạn bởi các đường 
1y x , trục hoành, 2, 5x x quanh trục Ox bằng: 
A. d
5
2
1x x B. d
5
2
1x x C. d
2
2
2
1
1y x D. d
5
2
1x x 
C©u 3 : 
Giá trị của d
2
2
0
2 xe x là: 
A. 4e B. 4 1e C. 44e D. 43 1e 
C©u 4 : 
Cho tích phân 4
20
6 tan
cos 3tan 1
x
I dx
x x



 . Giả sử đặt 3tan 1u x  thì ta được: 
A.  
2
2
1
4
2 1
3
I u du  . B.  
2
2
1
4
1
3
I u du  . 
C.  
2
2
1
4
1
3
I u du  . D.  
2
2
1
4
2 1
3
I u du  . 
C©u 5 : 
Nếu 
6
0
( ) 10f x dx và 
4
0
( ) 7f x dx , thì 
6
4
( )f x dx bằng : 
A. 3 B. 17 C. 170 D. 3 
C©u 6 : 
Họ nguyên hàm của hàm số  
3
21
x
f x
x


 là: 
A.  2 2
1
2 1
3
x x C   B.  2 2
1
1 1
3
x x C    
www.MATHVN.com - Toán học Việt Nam
Nguồn: Group Nhóm Toán FB
 2 
C.  2 2
1
1 1
3
x x C   D.  2 2
1
2 1
3
x x C    
C©u 7 : 
Giả sử 
d
5
1
ln
2 1
x
c
x
. Giá trị đúng của c là: 
A. 9 B. 3 C. 81 D. 8 
C©u 8 : Tính diện tích  S hình phẳng được giới hạn bởi các đường: 
2 2
4 ;
4 4 2
x x
y y   . 
A. 
2
2
3
S   . B. 
5
2
3
S   . C. 
4
2
3
S   . D. 
1
2
3
S   . 
C©u 9 : 
Nếu (1) 12, '( )f f x liên tục và 
4
1
'( ) 17f x dx , giá trị của (4)f bằng: 
A. 29 B. 5 C. 19 D. 9 
C©u 10 : 
Nếu ( )f x liên tục và 
4
0
( ) 10f x dx , thì 
2
0
(2 )f x dx bằng : 
A. 5 B. 29 C. 19 D. 9 
C©u 11 : 
Biết  
0
2 4 0
b
x dx  , khi đó b nhận giá trị bằng: 
A. 1b  hoặc 4b  B. 0b  hoặc 2b  
C. 1b  hoặc 2b  D. 0b  hoặc 4b  
C©u 12 : 
Cho d
6
0
1
sin cos
64
nI x x x . Khi đó n bằng: 
A. 5 B. 3
C. 4
D. 6 
C©u 13 : Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2y x và đường thẳng 2y x bằng: 
A. 
23
15
 B. 
4
3
 C. 
3
2
 D. 
5
3
C©u 14 : Thể tích của khối tròn xoay tạo lên bởi lên hình phẳng (H) giới hạn bởi các đường 2 2y x   
; 1y  và trục Ox khí quay xung quanh Ox là 
www.MATHVN.com - Toán học Việt Nam
Nguồn: Group Nhóm Toán FB
 3 
A. 
1 1
2 2
1 1
( 1)x dx dx 
 
    B. 
1 1
2 2
1 1
( 2)x dx dx 
 
    
C. 
1 1
2 2
1 1
( 2)x dx dx 
 
    D. 
1
2 2
1
( 2)x dx

  
C©u 15 : 
Cho 2
4
( ) sin
m
f x x

  . Tìm m để nguyên hàm F(x) của f(x) thỏa mãn F(0) = 1 và 
4 8
F
  
 
 
A. B. C. D. 
C©u 16 : 
Khẳng định nào sau đây đúng về kết quả 3
1
3 1
ln
e ae
x xdx
b
 ? 
A. . 64a b B. . 46a b C. 12a b D. 4a b 
C©u 17 : 
Khẳng định nào sau đây đúng về kết quả 
1 3
4
0
1
ln2
1
x
dx
ax
? 
A. 2a B. 4a C. 4a D. 2a 
C©u 18 : 
Cho các hàm số: 
220 30 7
( )
2 3
x x
f x
x
 


;    2 2 3F x ax bx x x    với 
3
2
x  . Để hàm số
 F x là một nguyên hàm của hàm số ( )f x thì giá trị của , ,a b c là: 
A. 4; 2; 1a b c   B. 4; 2; 1a b c     
C. 4; 2; 1a b c    . D. 4; 2; 1a b c    
C©u 19 : 
Tính tích phân 
1
2
0
(3 1)
6 9
x dx
I
x x


 
A. 
4 5
3ln
3 6
 B. C. 
4 5
3ln
3 6

 D. 
4 7
3ln
3 6
 
C©u 20 : Một nguyên hàm ( )cos3 1( 2)sin3 sin3 2017x a xx xdx x
b c
 thì tổng .S a b c bằng : 
A. 14S B. 15S C. 3S D. 10S 
C©u 21 : 
Tìm họ nguyên hàm: ( )
2ln 1
dx
F x
x x


 
A. ( ) 2 2ln 1F x x C   B. ( ) 2ln 1F x x C   
C. 
1
( ) 2ln 1
4
F x x C   D. 
1
( ) 2ln 1
2
F x x C   
4
3
m  
3
4
m 
3
4
m  
4
3
m 
3 5
3ln
4 6

www.MATHVN.com - Toán học Việt Nam
Nguồn: Group Nhóm Toán FB
 4 
C©u 22 : 
Nguyên hàm của hàm số   2 – 3 
1
 f x x x
x
  là 
A. F(x) = 
3 23
ln
3 2
x x
x C   B. F(x) = Cx
xx
 ln
2
3
3
23
C. F(x) = 
3 23
ln
3 2
x x
x C   D. F(x) = 
3 23
ln
3 2
x x
x C   
C©u 23 : Thể tích của khối tròn xoay sinh ra khi quay quanh trục Oy hình phẳng giới hạn bởi các 
đường: 2y x 4x 3   và Ox bằng: 
A. 
16
5

 B. 5 C. 
5

 D. 
16
3

C©u 24 : 
Cho   2
2
1
x
f x
x


. Khi đó: 
A.    22ln 1f x dx x C   B.    
23ln 1f x dx x C   
C.    24ln 1f x dx x C   D.    
2ln 1f x dx x C   
C©u 25 : Cho hai hàm số y = f(x), y = g(x) có đồ thị (C1) và (C2) liên tục trên [a;b] thì