Một số kiến thức Hình học THPT

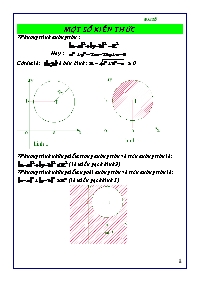
MOÄT SOÁ KIEÁN THÖÙC 
*Phöông trình ñöôøng troøn :
	Hay : 
Coùtaâm laø: vaø baùn kính : 0 
*Phöông trình nhöõng ñieåm trong ñöôøng troøn vaø treân ñöôøng troøn laø: 
 ( laø mieàn gaïch hình 2) 
*Phöông trình nhöõng ñieåm ngoaøi ñöôøng troøn vaø treân ñöôøng troøn laø: (laø mieàn gaïch hình 3)
*Ñöôøng thaúng : ax + by + c = 0 chia maët phaúng toïa ñoä thaønh 2 phaàn ax + by + c 0 vaø ax + by + c 0 ñeå bieát phaàn naøo lôùn hôn 0 hay nhoû hôn 0, thoâng thöôøng ta laáy 1 ñieåm treân mieàn theá vaøo. Neáu khoâng thoaû ta laáy mieàn ngöôïc laïi .
Xeùt ñöôøng thaúng : -x + y – 2 0 (nhö hình veõ).Ta laáy ñieåm (0;0) theá vaøo (-x + y – 2) ta ñöôïc -2 0 . Neân ta laáy mieàn chöùa (0;0) ñoù chính laø mieàn gaïch nhö treân hình veõ 
* cho haøm soá : y = f(x) coù mxñ laø D , gtnn = m ,gtln = M ta noùi:
Haøm soá y = f(x) coù nghieäm khi : m y M trong mxñ
f(x) coù nghieäm khi M trong mxñ 
f(x) ñuùng x khi m trong mxñ 
f(x) coù nghieäm khi m trong mxñ
f(x) ñuùng x khi M trong mxñ
*Cho A(x0 , y0 ) vaø ñöôøng thaúng () coù phöông trình : ax + by + c = 0 , khoaûng caùch töø A ñeán ñöôøng thaúng laø :
 d(A; ) = 
*Coâng thöùc ñoåi truïc : [ gs I(a;b) ]
 Ñoåi truïc oxy IXY
phaàn1 GIAÛI BAÈNG PHÖÔNG PHAÙP ÑOÀ THÒ
Tìm m ñeå heä phöông trình sau coù nghieäm.
Giaûi :
Ñaët u = sinx , v = siny 
Baøi toaùn trô ûthaønh tìm m ñeå heä sau coù nghieäm :
(*)
Caùc ñieåm thoûa (3)(4) laø nhöõng ñieåm naèm treân vaø trong hình vuoâng ABCD nhö hình veõ ,(2) laø phöông trình ñöôøng troøn taâm I(0,0) baùn kính R = , do soá giao ñieåm cuûa ñöôøng thaúng vaø ñöôøng troøn chính laø soá nghieäm . Vaäy ñeå heä phöông trình coù nghieäm ñöôøng troøn phaûi caét ñöôøng thaúng u + v = naèm trong hình vuoâng. Deã thaáy 
M(1 ; -) vaø OM = ON
OM = , OH = = , suy ra ycbt laø
- m 
Cho heä phöông trình.
 (*)
a) tìm taát caû caùc giaù trò cuûa a ñeå heä coù 2 nghieäm phaân bieät.
b)goïi (x1 ; y1) , (x2 ; y2 ) laø 2 nghieäm cuûa heä ,chöùng minh raèng .
 (x2 – x1)2 + (y2 – y1)2 1
Giaûi :
a) Heä ñaõ cho coù theå vieát laïi :
(*) 
Ta nhaän thaáy (1) laø phöông trình ñöôøng thaúng ,luoân qua ñieåm coá ñònh (0;1) . (2) laø phöông trình ñöôøng troøn coù taâm I(;0) baùn kính R = . Do soá giao ñieåm cuûa ñöôøng thaúng vaø ñöôøng troøn chính laø soá nghieäm . Vaäy ñeå heä phöông trình coù 2 nghieäm khi :
D(I ;d) = < 
 0 <m < 
b) ta coù AB = 2R
 (x2 –x1)2 + (y2 – y1)2 4R =1 (ñpcm)
Daáu (=) xaûy ra khi ñöôøng thaúng qua taâm :
Hay : - a = 0 a = 
Cho heä phöông trình.
 (*)
Tìm a sao cho heä sau ñaây coù nghieäm.
Giaûi :
Heä ñaõ cho coù theå vieát laïi :
Caùc ñieåm M(x;y) thoûa(1) laø nhöõng ñieåm naèm treân 2 ñöôøng thaúng nhö hình veõ
Caùc ñieåm M(x;y) thoûa (2) laø nhöõng ñieåm naèm treân 2 mieàn gaïch 
Ta coù A(-2;0) , B(-2;3) , C(-1;2) , D(1;0) , E(2;-1) , F(-1;-1) , K(1;-3) , M(2;-4) .
Vaäy töø ñoà thò heä coù nghieäm khi : -4<a<-3 , -1<a<0 , 2<a<3.
Cho heä phöong trình.
 (*)
Tìm m sao cho heä sau ñaây coù 3 nghieäm .
Giaûi :
Heä ñaõ cho coù theå vieát laïi :
(*) 
Caùc ñieåm M(x;y) thoûa (1) laø nhöõng ñieåm naèm treân 2 ñöôøng thaúng nhö hình veõ
Caùc ñieåm M(x;y) thoûa (2) laø nhöõng ñieåm naèm treân ñöôøng troøn taâm I(0;0) baùn kính R = , do soá giao ñieåm cuûa ñöôøng thaúng vaø ñöôøng troøn chính laø soá nghieäm . Vaäy ñeå heä phöông trình coù 3 nghieäm thì :
R = ON , maø ON = = (aùp duïng ñktx) do ñoù :
 = 
Bieän luaän theo a veà soá nghieäm cuûa phöông trình.
Giaûi :
Ta ñoåi truïc cho deã veà vieäc tính toaùn vaø bieän luaän:
Ñoåi truïc oxy 0XY 
Heä ñaõ cho coù theå vieát laïi :
Ta nhaän thaáy caùc ñieåm M(x;y) thoaû maõn (1) laø hình vuoâng A,B,C,D trong ñoù A(-2;0) , B(0;2) , C(2;0) , D(0;-2) .Caùc ñieåm thoûa maõn (2) naèm treân 2 ñöôøng: X = 2a ,Y= 2a , maø giao ñieåm I cuûa chuùng luoân luoân di ñoäng treân Y = X , deã thaáy ñieåm I/(1;1) nhö hình veõ , do soá giao ñieåm cuûa 2 ñöôøng thaúng vaø hình vuoâng ABCD chính laø soá nghieäm .
neân ta coù : 
 Neáu heä voâ nghieäm.
Neáu heä coù 2 nghieäm.
Neáu heä coù 4 nghieäm.
 Neáu heä coù 3 nghieäm.
Tìm a ñeå phöông trình sau coù 2 nghieäm .
 (*)
Giaûi :
Vôùi ñieàu kieän x – x2 0 , ñaët y = 0
(*) trôû thaønh 
(2) vaø (3) laø phöông trình nöûa ñöôøng troøn laáy phaàn döông nhö hình veõ , coù taâm I(;0) baùn kính R = . (1) laø phöông trình ñöôøng thaúng x +y = a , do soá giao ñieåm cuûa ñöôøng thaúng vaø ñöôøng troøn chính laø soá nghieäm . Vaäy ñeå heä phöông trình coù 2 nghieäm thì ñöôøng thaúng x +y = a phaûi lôùn hôn hoaëc baèng x + y = 1 vaø nhoû hôn tieáp xuùc treân , maø tieáp xuùc treân baèng .
hay 0 a <
ñònh a ñeå phöông trình sau coù 4 nghieäm .
2 (*)
Giaûi :
Ñaët 
(*)
Nhaän xeùt t thì ta ñöôïc 2 nghieäm x , theo ycbt ta caàn coù 2 nghieäm t
Deã thaáy A() (1) laø phöông trình y = -3t ñeå thoaû baøi toaùn thì ()
(2) laø phöông trình ñöôøng thaúng y = t , 0
Vaäy ñeåâ phöông trình coù 4 nghieäm x hay coù 2 nghieäm t thì: 
Cho heä baát phöong trình.
 (*)
Tìm a ñeå heä coù nghieäm duy nhaát .
Giaûi :
Baát phöông trình (1) laø nhöõng ñieåm naèm treân vaø trong ñöôøng troøn taâm O2(0;-1) baùn kính R2 =. (nhö hình veõ) 
Baát phöông trình (2) laø nhöõng ñieåm naèm treân vaø trong ñöôøng troøn taâm O1(-1;0) baùn kính R1 = .
Vaäy heä coù nghieäm duy nhaát khi : R1 + R2 = O1O2 
Hay : 2= 
Tìm m ñeå heä baát phöông trình sau coù nghieäm duy nhaát.
Giaûi :
Heä (*) cho coù theå vieát laïi .
Xeùt heä toaï ñoä tröïc chuaån oxa.
Töø hình veõ coù theå thaáy caùc ñieåm M(x;a) thoûa maõn (1) vaø (2) laø mieàn gaïch cheùo naèm treân vaø trong hình thang ABCD .Vaäy heä baát phöông trình coù nghieäm duy nhaát khi :
a = 1 hoaëc a = 5
Tìm m ñeå heä phöông trình coù 8 nghieäm.
Giaûi :
Ta ñoåi truïc cho deã veà vieäc tính toaùn vaø bieän luaän.
Ñoåi truïc oxy 0XY
Heä ñaõ cho coù theå vieát laïi .
Caùc ñieåm M(x;y) thoûa (1) laø nhöõng ñieåm naèm treân hình vuoâng ABCD , nhö hình veõ .Caùc ñieåm M(x;y) thoûa (2) laø phöông trình ñöôøng troøn taâm O(0;0) baùn kímh R = . Do soá giao ñieåm cuûa ñöôøng thaúng vaø ñöôøng troøn chính laø soá nghieäm . Vaäy ñeå heä phöông trình coù 8 nghieäm khi : OH < R < OB .
Maø : OH = ( aùp duïng ñktx) , OB = 1 .
Vaäy < < 1 ñoù laø ycbt
Bieän luaän soá nghieäm cuûa phöông trình . 
Giaûi :
Vôùi ñieàu kieän 12 – 3x2 0 ñaët y = . Phöông trình coù theå vieát laïi 
Coù theå thaáy caùc ñieåm M(x;y) thoûa (1) vaø (2) laø phöông trình cuûa nöûa ellip laáy phaàn döông , nhö treân hình veõ . Coù theå thaáy caùc ñieåm M(x;y) thoûa (3) laø phöông trình ñöôøng thaúng luoân di ñoäng vaø coù heä soá goùc laø -1 .
Xeùt caùc vò trí tôùi haïn cuûa noù : qua A öùng vôùi m = -1
Vò trí tieáp xuùc treân 
Taïi B öùng vôùi m = 1
Vaäy ta coù : Neáu 1 m <2 phöông trình coù 2 nghieäm.
 Neáu m = 2 hoaëc -1 m <1 phöông trình coù 1 ngieäm.
 Neáu m > 2 hoaëc m<-1 phöông trình voâ nghieäm.
Cho heä : 
a) tìm a ñeå heä coù nghieäm.
b) tìm a ñeå heä coù nghieäm duy nhaát.
Giaûi :
Heä ñaõ cho coù theå vieát lai .
Caùc ñieåm M(x;a) thoûa maõn (1) vaø (2) naèm trong mieàn gaïch cheùo ta coù, S1(2;) , S2(-1;1) vaø 
xA = -< 1
töø hình veõ, heä ñaõ cho coù nghieäm khi . 0
heä ñaõ cho coù nghieäm duy nhaát khi .
tìm m ñeå heä baát phöông trình sau coù nghieäm duy nhaát .
Giaûi :
Heä ñaõ cho coù theå vieát thaønh .
Xeùt heä toaï ñoä tröïc chuaån oxy
Nhaän xeùt : nhöõng ñieåm M(x;y) thoûa maõn (1) laø nhöõng ñieåm naèm treân vaø trong ñöôøng troøn taâm I(1;1) baùn kính R = (nhö hình veõ) , nhöõng ñieåm M(x;y) thoûa maõn (2) laø mieàn gaïch cheùo vaø ñöôøng thaúng x +y =1 .Vaäy heä coù nghieäm duy nhaát khi vaø chæ khi R = OH ,
Maø OH = ( aùp duïng ñktx) vaäy : laø ycbt
tìm m ñeå heä baát phöông trình sau coù nghieäm.
Giaûi :
Heä ñaõ cho coù theå vieát thaønh .
phöông trình m = -x2 + 2x +4 laø parabol coù ñænh S(1;5) nhö hình veõ do ñoù caùc ñieåm M(x;y)thoaû (1 ) laø nhöõng ñieåm naèm trong parabol chöùa mieàn thoûa (0;0) .
Xeùt haøm soá:
 	m = x4 -6x2 -8x+18
mxñ:	D = R 
Ñaïo haøm :
	m/ = 4x3 -12x-8 = 4(x+1)2(x-2)
 m/ = 0 
baûng bieán thieân .
Haøm soá ñaït cöïc tieåu taïi . 
Ñieåm ñaëc bieät (1;5) ; (3;5) 
caùc ñieåm M(x;y) thoaû maõn (*) laø mieàn gaïch cheùo nhö hình veõ . töø ñoà thò ta thaáy heä coù nghieäm khi ñöôøng thaúng y = m caét mieàn gaïch cheùo, hay - 
Cho heä : 
a) tìm a ñeå heä coù nghieäm.
b) tìm a ñeå heä coù nghieäm duy nhaát.
Giaûi :
Heä ñaõ cho coù theå vieát laïi .
Xeùt heä toaï ñoä tröïc chuaån oxa .
Deã nhaän thaáy A(-2;0) , B(-;) O1(;) , F(--)
M(x;a) thoûa maõn (1) vaø (2) laø nhöõng ñieåm naèm trong mieàn gaïch soïc nhö hình veõ, nhö vaäy ñeå heä phöông trình coù nghieäm ñöôøng thaúng y =a phaûi caét mieàn gaïch soïc .
Vaäy theo ycbt thì 
a) heä coù nghieäm khi -
b) heä coù nghieäm duy nhaát khi a = - hoaëc a = - hoaêc a = 
Cho heä : 
a) tìm m ñeå heä coù nghieäm.
b) tìm m ñeå heä coù nghieäm duy nhaát.
Giaûi :
Heä ñaõ cho coù theå vieát laïi nhö sau .
Xeùt heä toaï ñoä tröïc chuaån oxm .
Caùc ñieåm M(x;m) thoûa maõn (1) naèm trong giôùi haïn cuûa 2 ñöôøng thaúng x =-2 vaø.x =, caùc ñieåm M(x;m) thoûa maõn (2) naèm trong mieàn gaïch soïc nhö hình veõ .Deã thaáy A() , vaäy ñeå phöông trình coù nghieäm thì ñöôøng thaúng m = phaûi caét mieàn gaïch soïc trong giôùi haïn cho pheùp cuõa (1) hay.
 a) heä coù nghieäm khi m 
 b) heä coù nghieäm duy nhaát khi . 
Tìm m ñeå heä phöông trình coù nghieäm.
Giaûi :
Ta ñoåi truïc cho deã veà vieäc tính toaùn vaø bieän luaän:
Ñoåi truïc oxy 0XY
Heä ñaõ cho coù theå vieát laïi .
Caùc ñieåm M(x;y) thoûa (1) laø nhöõng ñieåm naèm treân hình vuoâng ABCD , nhö hình veõ .Caùc ñieåm M(x;y) thoûa (2) laø phöông trình ñöôøng troøn taâm O(-1;-1) baùn kímh R = . Do soá giao ñieåm cuûa ñöôøng thaúng vaø ñöôøng troøn chính laø soá nghieäm . Vaäy ñeå heä phöông trình coù nghieäm khi : ON R OM .
Maø : ON = ( aùp duïng ñktx) , OB = .
Vaäy ñoù laø ycbt
MOÄT SOÁ BAØI TAÄP
Tìm m ñeå phöông trình coù nghieäm
Cho phöông trình .
a) tìm gtln vaø gtnn 
b) tìm m ñeå phöông trình coù nghieäm .
Cho heä 
tìm a ñeå heä coù nghieäm.
Tìm m ñeå baát phöông trình sau ñuùng 
Cho heä 
tìm m ñeå heä voâ nghieäm.
Cho heä 
tìm m ñeå heä coù nghieäm.
Tìm m ñeå baát phöông trình sau coù nghieäm.
loga+x(x(a-x)) < loga+x x
Cho heä phöong trình.
 (*)
a) tìm taát caû caùc giaù trò cuûa a ñeå heä coù 2 nghieäm phaân bieät.
b) goïi A(x1 ; y1) , B(x2 ; y2 ) laø 2 nghieäm cuûa heä .Tìm a ñeå ñoä daøi daây cung AB ñaït giaù trò lôùn nhaát .
phaàn2 HEÄ PHÖÔNG TRÌNH 
Xeùt ña thöùc vôùi bieán laø x,y goïi F(x;y) .Neáu ta coù F(x;y) = F(y;x) vôùi moi x ,y R thì F(x;y) laø ña thöùc ñoái xöùng:
Ñoái xöùng loaïi 1 .(neáu thay x bôûi y vaø thay y bôûi x phöông trình (1) vaån laø phöông trình (1) vaø phöông trình (2) vaån laø phöông trình (2) )
Ñoái xöùng loaïi 2 .(neáu thay x bôûi y vaø thay y bôûi x phöông trình (1 ) trôû thaønh (2)vaø phöông trình (2) trôû thaønh (1))
Baøi taäp ñoái xöùng loai 
Giaûi heä phöông trình .
Giaûi :
Heä ñaõ cho coù theå vieát laïi nhö sau .
ñaët ñieàu kieän S2 4P
Heä phöông trình töông ñöông vôùi .
Giaûi heä phöông trình .
Giaûi :
(Ta cöù coi z nhö laø tham soá , ta ñöôïc heä ñoái xöùng loaïi 1 )
Heä ñaõ cho coù theå vieát laïi nhö sau .
Ñeå phöông trình coù nghieäm x,y khi
Neáu z heä voâ nghieäm
Neáu z =1 thì 
Vaäy heä coù nghieäm x = 0 ,y = 0 , z = 1 .
Cho heä phöông trình .
 a) giaûi heä vôùi m = 5
 b) vôùi giaù trò naøo cuûa m thì heä coù nghieäm .
Giaûi :
Heä ñaõ cho coù theå vieát laïi nhö sau .
ñaët ñieàu kieän S2 4P
vôùi m = 5 
ñeå heä phöông trình coù nghieäm.
th1: .
 hay 
 2
th2: .
hay 
3deã thaáy baát phöông trình voâ nghieäm vì 
Vaäy ñeå heä phöông trình coù nghieäm khi ñoù laø ycbt.
Baøi taäp ñoái xöùng loai 2
Giaûi heä phöông trình .
Giaûi :
Heä ñaõ cho coù theå vieát laïi nhö sau .
Haûy xaùc ñònh a ñeå heä sau coù nghieäm duy nhaát .
Giaûi :
xeùt ñieàu kieän caàn :
Nhaän xeùt raèng neáu heä phöông trình coù nghieäm (x;y) thì heä phöông trình cuõng coù nghieäm (y;x) .Vaäy ñeå heä phöông trình coù nghieäm duy nhaát thì x = y ,ta ñöôïc
x2 + x = ax2 + 1 (a- 1)x2 –x + 1 = 0 (1)
phöông trình (1) coù nghieäm duy nhaát
xeùt ñieàu kieän ñuû : 
vôùi a =1 heä coù daïng : 
 vaäy a=1 loai .
vôùi a =heä coù daïng : deã nhaän thaáy heä coù ít nhaát 2 nghieäm thoaû nhö (1;0) , (0;1) . Vaäy vôùi a =khoâng thoûa 
keát luaän : khoâng toàn taïi a ñeå heä coù nghieäm duy nhaát 
Giaûi heä .
Giaûi :
Ñieàu kieän :
Heä ñaõ cho coù theå vieát laïi nhö sau .
a 0 heä voâ nghieäm 
a > 0 (1) 
Heä ñaúng caáp.
Giaûi heä phöông trình .
Giaûi :
Ñieàu kieän : x0 , y0
Heä ñaõ cho coù theå vieát laïi nhö sau .
vaäy heä coù 2 nghieäm . 
Giaûi heä phöông trình .
Giaûi :
Nhaän xeùt phöông trình khoâng coù nghieäm (x;0) .
Ta coù : 
Vaäy heä phöông trình coù 4 nghieäm nhö treân.
Giaûi heä phöông trình .
Giaûi :
Deã daøng nhaän thaáy heä khoâng coù nghieäm (x;0) .
Do ñoù 
MOÄT SOÁ BAØI TAÄP .
Giaûi heä phöông trình .
a) Giaûi heä vôùi m = 1 
b)Vôùi nhöõng giaù trò naøo cuûa m thì heä coù nghieäm
chöùng toû raèng vôùi a0 , heä coù nghieäm duy nhaát .
Cho (x;y;z) laø nghieäm cuûa heä phöông trình 
Chöøng minh raèng . 
Tìm a ñeå heä sau ñaây coù nghieäm.
Tìm a ñeå heä sau ñaây coù nghieäm duy nhaát.
Giaûi heä phöông trình .
Giaûi heä phöông trình .
Giaûi heä phöông trình .
Tìm a ñeå heä sau ñaây coù nghieäm.
Cho heä phöông trình.
a) giaûi heä m=3
b) chöùng minh raèng vôùi moïi m heä phöông trìmh luoân coù nghieäm
Moät soá daïng thöôøng gaëp khaùc.
 Giaûi heä phöông trình .
Giaûi :
Heä ñaõ cho coù theå vieát laïi nhö sau .
Vì neân deã nhaän thaáy (2) voâ nghieäm .
Giaûi heä phöông trình .
Giaûi :
Heä ñaõ cho coù theå vieát laïi nhö sau .
 xeùt coù = neân (2) voâ nghieäm 
Tìm caùc soá x,y thuoäc khoaûng (0;) thoûa maõn heä.
Giaûi :
Xeùt haøm soá y = cotgx – x vôùi x 
y/ = - ( cotg2x + 1) – 1 < 0 x . Vaäy haøm soá luoân luoân giaûm
do ñoù phöông trình cotgx – x = cotgy – y coù nghieäm duy nhaát x = y
Phöông trình aån ñoái xöùng
Giaûi phöông trình .
 (*)
Giaûi :
 ñaët 
Deã daøng thaáy phöông trình voâ nghieäm vì < 0
hay 
Giaûi phöông trình .
 (*)
Giaûi :
 ñaët 
Phöông trình voâ nghieäm vì 
Phaàn 3 ÑIEÀU KIEÄN CAÀN VAØ ÑUÛ.
(coù theå giaûi nhöõng baøi phi tuyeán)
Caàn phaùt hieän ñieàu kieän caàn hôïp lí.Choïn ñieàu kieän ñuû .
Tìm a ñeå heä sau ñaây coù nghieäm duy nhaát.
Giaûi :
* ñieàu kieän caàn.
Giaû söû heä coù nghieäm duy nhaát (x;y) thì heä cuõng coù nghieäm (-x;y) ,do tính duy nhaát cuûa nghieäm neân heä coù nghieäm duy nhaát khi . x = -x x = 0 . 
Thay vaøo (*) ta ñöôïc 
*ñieàu kieän ñuû .
Vôùi a = 2 heä (*) trôû thaønh .
deã nhaän thaáy heä coù nghieäm (1;0) , (-1;0) neân a = 0 khoâng thoûa .
Vôùi a = 2 heä (*) trôû thaønh .
Vaäy (3)(4) 
Vaäy theo ycbt thì : a = 0 
Tìm a ñeå heä sau ñaây coù nghieäm vôùi moïi b .
Giaûi :
* ñieàu kieän caàn.
Giaû söû heä coù nghieäm b töùc coù nghieäm vôùi b = 0 , ta ñöôïc
*ñieàu kieän ñuû .
Vôùi a = 0 heä (*) trôû thaønh 
neáu b 0 suy ra y = 0 ta nhaän thaáy (2) khoâng thoûa maõn .
Vaäy b 0 vaø a = 0 khoâng thoaû maõn ycbt .
Vôùi a = 1 heä (*) trôû thaønh 
 roõ raøng b (3)(4) luoân luoân thoûa maõn 
Vaäy a = 1 laø ñieàu kieän caàn vaø ñuû ñeå thoaû ycbt .
Tìm a ñeå heä sau ñaây coù nghieäm vôùi moïi b .
Giaûi :
* ñieàu kieän caàn.
Giaû söû heä coù nghieäm b töùc coù nghieäm vôùi b = 0 , ta ñöôïc
*ñieàu kieän ñuû .
Vôùi a = 1 heä (*) trôû thaønh 
Deã nhaän thaáy b phöông trìmh voâ nghieäm . Vaäy a = 1 khoâng thoûa maõn .
Vôùi a = -1 heä (*) trôû thaønh 
roõ raøng b heä (3)(4) luoân luoân nhaän laø nghieäm 
Vaäy a = -1 laø ñieàu kieän caàn vaø ñuû ñeå thoûa maõn ycbt .
Tìm a ñeå heä sau ñaây coù nghieäm duy nhaát.
Giaûi :
* ñieàu kieän caàn.
Giaû söû heä coù nghieäm duy nhaát (x;y) thì heä cuõng coù nghieäm (-x;y) ,do tính duy nhaát cuûa nghieäm neân heä coù nghieäm duy nhaát khi . x = -x x = 0 .
Thay vaøo (*) ta ñöôïc 
* ñieàu kieän ñuû 
Vôùi a = 0 heä (*) trôû thaønh 
 heä naøy voâ soá nghieäm tuøy theo giaù trò cuûa k 
Vaäy a = 0 khoâng thoaû maõn ycbt
Vôùi a = 2 heä (*) trôû thaønh 
(1)(2) 
Vaäy a = 2 laø ñieàu kieän caàn vaø ñuû ñeå thoûa maõn 
Tìm m ñeå phöông trình sau ñaây coù nghieäm duy nhaát.
Giaûi :
* ñieàu kieän caàn.
Neáu (*) coù nghieäm x = x0 thì (*) cuõng coù x = 1 - x0 do tình duy nhaát cuûa nghieäm neân ñeå phöông trình coù nghieäm duy nhaát khi x0 = 1 - x0 hay x0 = 
Thay vaøo (*) ta ñöôïc . m = 
* ñieàu kieän ñuû
Vôùi m = (*) trôû thaønh 
Theo baát ñaúng thöùc Bunhiakoápki thì . 
 (1)
 (2)
töø (1) vaø (2) ñeå thoaû (*) ta caàn ñaúng thöùc (1) vaø (2) xaûy ra ñoàng thôøi , hay
Toùm laïi phöông trình coù nghieäm duy nhaát khi 
 m = 
Tìm x ñeå phöông trình sau nhgieäm ñuùng 
Giaûi :
* ñieàu kieän caàn.
Phöông trình (*) ñuùng neân ñuùng vôùi a = 0 , ta coù 
Vaäy (1) 
*ñieàu kieän ñuû .
Vôùi x = 1 (*) trôû thaønh 
 .(2) hieån nhieân ñuùng 
Vôùi (*) trôû thaønh .
Deã daøng nhaän thaáy (3) chæ ñuùng vôùi a = 0 , neân khoâng thoûa maõn ycbt
Toùm laïi ñieàu kieän caàn vaø ñuû laø x = 1 .
Tìm x ñeå phöông trình sau nhgieäm ñuùng 
Giaûi :
* ñieàu kieän caàn.
Phöông trình (*) ñuùng neân ñuùng vôùi a = 0 , ta coù 
* ñieàu kieän ñuû .
Vôùi x = 2 (*) trôû thaønh . (*). phöông trình khoâng theå ñuùng vì ñieàu kieän vaäy vôùi x = 2 khoâng thoûa maõn ycbt.
Vôùi x = 5 (*) trôû thaønh 
(*) . roõ raøng phöông trình ñuùng 
Toùm laïi ñieàu kieän caàn vaø ñuû laø x = 5 .
Tìm m ñeå phöông trình sau ñaây coù nghieäm duy nhaát.
Giaûi :
*ñieàu kieän caàn .
Neáu phöông trình (*) coù nghieäm x = x0 thì phöông trình (*) cuõng coù nghieäm 
x = 4 - x0 do tính duy nhaát cuûa nghieäm neân , ñeå phöông trình coù nghieäm duy nhaát thì x0 = 4 - x0 x0 = 2
vôùi x0 = 2 ta ñöôïc .
* ñieàu kieän ñuû .
Vôùi m = 1 (*) trôû thaønh 
 thoûa maõn ycbt.
Toùm laïi ñieàu kieän caàn vaø ñuû laø m = 1 .
Tìm a ñeå heä sau ñaây coù nghieäm.
Giaûi :
*ñieàu kieän caàn .
Giaû söû heä coù nghieäm (x;y) hay .
 suy ra 
* ñieàu kieän ñuû .
Vôùi 
Ta coù 
Coù nghieäm thì (*) coù nghieäm vì moïi nghieäm (1) (2) ñeàu laø nghieäm cuûa heä (*)
Xeùt heä (1) (2) 
 heä coù nghieäm .Vaäy ñieàu kieän caàn vaø ñuû laø 
Tìm b ñeå heä sau ñaây coù nghieäm.
Giaûi :
*ñieàu kieän caàn .
Giaû söû heä coù nghieäm (x;y) hay . 
 suy ra 
* ñieàu kieän ñuû .
Vôùi ta coù
Coù nghieäm thì (*) coù nghieäm vì moïi nghieäm ñeàu laø nghieäm cuûa heä (*)
Xeùt heä (1) (2) 
heä coù nghieäm . 
Vaäy ñieàu kieän caàn vaø ñuû laø 
Tìm a ñeå heä sau ñaây coù nghieäm.
Giaûi :
* ñieàu kieän caàn .
Giaû söû heä coù nghieäm (x;y) hay .
 suy ra 
* ñieàu kieän ñuû .
Vôùi ta coù 
Coù nghieäm thì (*) coù nghieäm vì moïi nghieäm ñeàu laø nghieäm cuûa heä (*)
Xeùt heä 
heä coù nghieäm .Vaäy ñieàu kieän caàn vaø ñuû laø 
MOÄT SOÁ BAØI TAÄP
Tìm a ñeå heä sau ñaây coù nghieäm.
Tìm a , b ñeå phöông trình sau ñaây coù nghieäm ñuùng x sao cho .
Tìm a ñeå heä sau ñaây coù nghieäm duy nhaát.
Phaàn 4 PHÖÔNG TRÌNH VAØ BAÁT PHÖÔNG TRÌNH 
Xeùt tam thöùc baäc hai f(x) = ax2 + bx + c =0 (1) , a 0 
Ta coù = b2 – 4ac . 
Vaäy (2)
Töø (2) suy ra moät soá keát quaû sau ñaây .
Ñònh lí 1 : neáu 0 
Ñònh lí 2: neáu = 0 thì phöông trình (1) coù nghieäm duy nhaát 
Ñònh lí 3: neáu > 0 thì phöông trình (1) coù 2 nghieäm 
Ôû ñònh lí (3) - neáu a.f(x) < 0 khi x1 < x < x2
 - neáu a.f(x) > 0 khi x x2
* töø ñoù ta thu ñöôïc moät soá heä quaû sau .
Heä quaû1 : treân truïc soá thöïc xeùt khoaûng maø khoâng laø nghieäm 
Neáu ta coù thì vaø 
 Heä quaû2 : treân truïc soá thöïc xeùt khoaûng maø khoâng laø nghieäm 
Neáu ta coù thì vaø 
Caùc soá a,b,c thoûa maõn ñieàu kieän .
5a+4b+6c=0 (1 )
Chöùng minh raèng phöông trình .
f(x) = ax2 + bx + c = 0 (2)
coù nghieäm .
Giaûi :
Neáu a = 0 (1) ta coù thay vaøo phöông trình (2) ta ñöôïc . vaäy luoân coù nghieäm 
Neáu a 0 . 
(1) (4a+2b +c) + ( a + 2b + 4c ) + c =0
f(2) + 4f() + f(0) af(2) + 4af() + af(0) =0 
Vaäy toàn taïi ít nhaát moät soá haïng aâm hoaëc 3 soáâ h