Một số dạng toán tính nhanh lớp 5 - Trường Tiểu học số 2 Ân Đức

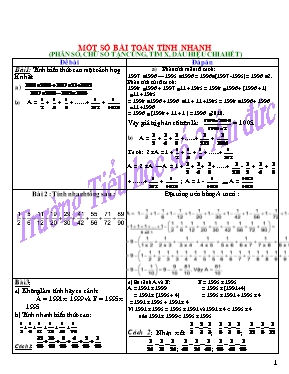
MỘT SỐ BÀI TOÁN TÍNH NHANH
(PHÂN SỐ, CHỮ SỐ TẬN CÙNG, TÌM X, DẤU HIỆU CHIA HẾT)
Đề bài
Đáp án
Bµi 1: TÝnh biÓu thøc sau mét c¸ch hîp lÝ nhÊt:
a) 
b) A = + + + ......+ + 
 a) Ph©n tÝch mÉu sè ta cã:
1997 1996 – 1995 1996 = 1996(1997 -1995) = 1996 2.
Ph©n tÝch tö sè ta cã:
1998 1996 + 1997 11 + 1985 = 1998 1996 + (1996 + 1) 11 + 1985
= 1998 1996 + 1996 11 + 11 +1985 = 1998 1996 + 1996 11 +1996
= 1996 (1998 + 11 + 1 ) = 1996 2010.
VËy gi¸ trÞ ph©n sè trªn lµ: = 1005.
b) A = + + + ......+ + 
Ta cã: 2 x A = 1 + + + + ......+ 
A = 2 x A – A = 1 + + + + .....+ - + + + ......+ + ; A = 1 - A = 
Bài 2 : Tính nhanh tổng sau : 
Đặt tổng trên bằng A ta có :
Bµi 3:
a) Kh«ng lµm tÝnh h·y so s¸nh:
A = 1991 x 1999 vµ B = 1995 x 1995
b) TÝnh nhanh biÓu thøc sau:
C¸ch 1: 
= 
= 
a) So s¸nh A vµ B: B = 1995 x 1995
A = 1991 x 1999 = 1995 x (1991+4)
 = 1991 x (1995 + 4) = 1995 x 1991 + 1995 x 4
 = 1991 x 1995 + 1991 x 4
V× 1991 x 1995 = 1995 x 1991 vµ 1991 x 4 < 1995 x 4
nªn 1991 x 1999 < 1995 x 1995
C¸ch 2: NhËn xÐt ; ; 	; ; 	
C = = 
 = 
C¸ch 3: NhËn xÐt:
	Do ®ã	
	Do ®ã: 
Cø theo quy luËt nµy ta cã:
C = = = 
Bµi 4 : Cho S = 
H·y so s¸nh S vµ .
XÐt c¸c sè h¹ng cña tæng ta thÊy : 
. Ta cã : 
>x10
 >
 Nªn S > .
Bài 5 :Tính nhanh:
( 1+3+5+7++2003+2005) x (125 125 x 127 – 127 127 x 125)
a) Ta có:
125 125x127 – 127 127x125 = 1001x125x127 – 1001x127x125 = 0 . nên : (1+3+5+...+2005)(125 125x127 – 127 127x125) = 0 
Bµi 6: Kh«ng quy ®ång tö sè vµ mÉu sè. H·y so s¸nh:
a/ ; b/ 
a/ Ta cã: ; 
Mµ v× hai ph©n sè cã cïng tö sè, ph©n sè nµo cã mÉu sè bÐ h¬n lµ ph©n sè lín h¬n. Suy ra: 
b/ suy ra 
Bài 7 : Cho 7 phân số : 
Thăng chọn được hai phân số mà tổng có giá trị lớn nhất. Long chọn hai phân số mà tổng có giá trị nhỏ nhất. Tính tổng 4 phân số mà Thăng và Long đã chọn. 
Vậy ta sắp xếp được như sau :
Tổng hai phân số có giá trị lớn nhất là : 
 Tổng hai phân số có giá trị nhỏ nhất là : 
Do đó tổng bốn phân số mà Thăng và Long đã chọn là : 
Bài 8 : Cho tổng : 
1 + 2 + 3 + 4 + 5 + ... + 49 + 50.
Liệu có thể liên tục thay hai số bất kì bằng hiệu của chúng cho tới khi được kết quả là 0 hay không ? 
Bài giải : Ta đặt A = 1 + 2 + 3 + 4 + 5 + ... + 49 + 50. Dãy số tự nhiên liên tiếp từ 1 đến 50 có 50 số, trong đó số các số lẻ bằng số các số chẵn nên có 50 : 2 = 25 (số lẻ). Vậy A là một số lẻ. Gọi a và b là hai số bất kì của A, khi thay tổng a + b bằng hiệu a - b thì A giảm đi : (a + b) - (a - b) = 2 x b tức là giảm đi một số chẵn. Hiệu của một số lẻ và một số chẵn luôn là một số lẻ nên sau mỗi lần thay, tổng mới vẫn là một số lẻ. Vì vậy không bao giờ nhận được kết quả là 0. 
Bài 9 : Viết liên tiếp các số từ trái sang phải theo cách sau : Số đầu tiên là 1, số thứ hai là 2, số thứ ba là chữ số tận cùng của tổng số thứ nhất và số thứ hai, số thứ tư là chữ số tận cùng của tổng số thứ hai và số thứ ba. Cứ tiếp tục như thế ta được dãy các số như sau : 1235831459437...... Trong dãy trên có xuất hiện số 2005 hay không ? 
Giả sử trong số tạo bởi cách viết như trên có xuất hiện nhóm chữ 2005 thì ta có : 2 + 0 là số có chữ số tận cùng là 0 (vô lí). 
Vậy trong dãy trên không thể xuất hiện số 2005.
Bµi 10: T×m x sao cho:
1,2 x ( - 0,05 ) = 1,44
 1,2 x ( - 0,05 ) = 1,44
( - 0,05) = 1,44 : 1,2
 - 0,05 = 1,2 nên = 1,2 + 0,05 
 = 1,25 do đó 2,4 x X – 0,23 = 1,25 x X
2,4 x X –1,25 x X = 0,23 nên X x (2,4 -1,25 ) = 0,23
 X = 0,23 : 1,15 Vậy X= 0,2
Bài 11: a) Tìm số tự nhiên bé nhất để thay vào x thì được: 
 3,15 x X > 15,5 3,15
b) Tìm số tự nhiên x biết rằng: 
c) 75% X + X + X = 30	
a) Tìm số tự nhiên bé nhất để thay vào x thì được: (0, 75 đ)
 X > 15,5 3,15
Hai tích có thừa số (*) giống nhau thì tích nào lớn hơn sẽ có thừa số còn lại lớn hơn.
Vậy; X > 15,5 mà vì X là số tự nhiên bé nhất nên X = 16
	b) Tìm số tự nhiên x biết rằng: ( 0, 75đ)
 ; ; 1< x< 3 ; Vậy x = 2
c) 0,75 X + 0,75 X + 1 X = 30	 
(0,75 + 0,75 + 1) X = 30 ; 2,5 X = 30	 X = 30 : 2,5 	 ; X= 12	
Bài 12 : Tìm các chữ số a và b thỏa mãn : 
Vì 1/3 là phân số tối giản nên a chia hết cho 3 hoặc b chia hết cho 3. Giả sử a chia hết cho 3, vì 1/a 3 mà a < 10 do đó a = 6 ; 9. 
Vậy a = b = 6.
Bài 13 : Tích sau đây có tận cùng bằng chữ số nào ?
Tích của bốn thừa số 2 là 2 x 2 x 2 x 2 = 16 và 2003 : 4 = 500 (dư 3) nên ta có thể viết tích của 2003 thừa số 2 dưới dạng tích của 500 nhóm (mỗi nhóm là tích của bốn thừa số 2) và tích của ba thừa số 2 còn lại. Vì tích của các thừa số có tận cùng là 6 cũng là số có tận cùng bằng 6 nên tích của 500 nhóm trên có tận cùng là 6. Do 2 x 2 x 2 = 8 nên khi nhân số có tận cùng bằng 6 với 8 thì ta được số có tận cùng bằng 8 (vì 6 x 8 = 48). Vậy tích của 2003 thừa số 2 sẽ là số có tận cùng bằng 8.
Bài 14 : Cho A = 2004 x 2004 x ... x 2004 (A gồm 2003 thừa số) và B = 2003 x 2003 x ... x 2003 (B gồm 2004 thừa số). Hãy cho biết A + B có chia hết cho 5 hay không ? Vì sao ? 
A = (2004 x 2004 x ... x 2004) x 2004 = C x 2004 (C có 2002 thừa số 2004). C có tận cùng là 6 nhân với 2004 nên A có tận cùng là 4 (vì 6 x 4 = 24). B = 2003 x 2003 x ... x 2003 (gồm 2004 thừa số) = (2003 x 2003 x 2003 x 2003) x ... x (2003 x 2003 x 2003 x 2003). Vì 2004 : 4 = 501 (nhòm) nên B có 501 nhóm, mỗi nhóm gồm 4 thừa số 2003. Tận cùng của mỗi nhóm là 1 (vì 3 x 3 = 9 ; 9 x 3 = 27 ; 27 x 3 = 81). Vậy tận cùng của A + B là 4 + 1 = 5. Do đó A + B chia hết cho 5.
Bµi 15: Cho tÝch sau:
0,9 x 1,9 x 2,9 x 3,9x  x 18,9
a, Kh«ng viÕt c¶ d·y, cho biÕt tÝch nµy cã bao nhiªu thõa sè ?
b, TÝch nµy tËn cïng b»ng ch÷ sè nµo?
c, TÝch nµy cã bao nhiªu ch÷ sè phÇn thËp ph©n?
a, Ta nhËn thÊy kho¶ng c¸ch gi÷a c¸c thõa sè liÒn nhau ®Ìu lµ 1 ®¬n vÞ nªu sè ®Çu lµ 0,9 -> thõa sè cuèi lµ 18,9 .VËy tÝch nµy cã 19 thõa sè .
b, V× tÝch nµy cã 19 thõa sè, mµ c¸c ch÷ sè cuèi cïng ®Òu lµ 9 nªn ch÷ sè cuèi cïng cña tÝch lµ ch÷ sè 9.
c,V× c¸c thõa sè ®Òu cã mét ch÷ sè phÇn thËp ph©n nªn tÝch nµy cã 19 ch÷ sè ë phÇn thËp ph©n.
Bài 16 : A là số tự nhiên có 2004 chữ số. A là số chia hết cho 9 ; B là tổng các chữ số của A ; C là tổng các chữ số của B ; D là tổng các chữ số của C. Tìm D. 
Vì A là số chia hết cho 9 mà B là tổng các chữ số của A nên B chia hết cho 9. Tương tự ta có C, D cũng chia hết cho 9 và đương nhiên khác 0. Vì A gồm 2004 chữ số mà mỗi chữ số không vượt quá 9 nên B không vượt quá 9 x 2004 = 18036. Do đó B có không quá 5 chữ số và C < 9 x 5 = 45. Nhưng C là số chia hết cho 9 và khác 0 nên C chỉ có thể là 9 ; 18 ; 27 ; 36. Dù trường hợp nào xảy ra thì ta cũng có D = 9. 
Bài 17 : Biết rằng số A chỉ viết bởi các chữ số 9. Hãy tìm số tự nhiên nhỏ nhất mà cộng số này với A ta được số chia hết cho 45. 
* Cách 1 : A chỉ viết bởi các chữ số 9 nên: 
Vậy A chia cho 45 dư 9. Một số nhỏ nhất mà cộng với A để được số chia hết cho 45 thì số đó cộng với 9 phải bằng 45. Vậy số đó là : 45 - 9 = 36. *Cách 2 : Gọi số tự nhiên nhỏ nhất cộng vào A là m. Ta có A + m là số chia hết cho 45 hay chia hết cho 5 và 9 (vì 5 x 9 = 45 ; 5 và 9 không cùng chia hết cho một số số nào đó khác 1). Vì A viết bởi các chữ số 9 nên A chia hết cho 9, do đó m chia hết cho 9. A + m chia hết cho 5 khi A + m có tận cùng là 0 hoặc 5 mà A có tận cùng là 9 nên m có tận cùng là 1 hoặc 6. Số nhỏ nhất có tận cùng là 1 hoặc 6 mà chia hết cho 9 là 36. Vậy m = 36. 
Bài 18 : Người ta lấy tích các số tự nhiên liên tiếp từ 1 đến 30 để chia cho 1000000. Bạn hãy cho biết : 
1) Phép chia có dư không ? 
2) Thương là một số tự nhiên có chữ số tận cùng là bao nhiêu ? 
Xét tích A = 1 x 2 x 3 x ... x 29 x 30, trong đó các thừa số chia hết cho 5 là 5, 10, 15, 20, 25, 30 ; mà 25 = 5 x 5 do đó có thể coi là có 7 thừa số chia hết cho 5. Mỗi thừa số này nhân với một số chẵn cho ta một số có tận cùng là số 0. Trong tích A có các thừa số là số chẵn và không chia hết cho 5 là : 2, 4, 6, 8, 12, . . . , 26, 28 (có 12 số). Như vật trong tích A có ít nhất 7 cặp số có tích tận cùng là 0, do đó tích A có tận cùng là 7 chữ số 0. Số 1 000 000 có tận cùng là 6 chữ số 0 nên A chia hết cho 1 000 000 và thương là số tự nhiên có tận cùng là chữ số 0. 
C©u 19: Khi chia 1095 cho mét sè tù nhiªn ta ®îc th¬ng lµ 7 vµ sè d lµ sè lín nhÊt cã thÓ. T×m sè chia.
Theo ®Ò bµi, phÐp chia 1096 cho mét sè tù nhiªn cã sè d lín nhÊt nªn khi sè bÞ chia céng thªm 1 th× ®îc sè míi sÏ chia hÕt cho sè chia cò. Khi ®ã th¬ng sÏ t¨ng thªm 1 ®¬n vÞ.
	VËy sè chia cÇn t×m lµ: (1905 + 1 ) : (7 + 1 ) = 137
Bài 20: ( 3 điểm) Tìm tất cả các số tự nhiên có 2 chữ số vừa chia hết cho 2 vừa chia hết cho 3 lại vừa chia hết cho 5?
Đặt điều kiện một số tự nhiên có 2 chữ số vừa chia hết cho 2 và vừa chia hết cho 5 là số có tận cùng là 0, vậy số đó là số tròn chục. 
Để các số tròn chục chia hết cho 3 thì chữ số hàng chục phải chia hết cho 3(1đ) Vậy các số đó là: 30; 60 ; 90. 
Bài 20 : Hai số tự nhiên A và B, biết A < B và hai số có chung những đặc điểm sau : - Là số có 2 chữ số. 
- Hai chữ số trong mỗi số giống nhau. 
- Không chia hết cho 2 ; 3 và 5. 
a) Tìm 2 số đó. 
b) Tổng của 2 số đó chia hết cho số tự nhiên nào ? 
Vì A và B đều không chia hết cho 2 và 5 nên A và B chỉ có thể có tận cùng là 1 ; 3 ; 7 ; 9. Vì 3 + 3 = 6 và 9 + 9 = 18 là 2 số chia hết cho 3 nên loại trừ số 33 và 99. A < B nên A = 11 và B = 77. 
b) Tổng của hai số đó là : 11 + 77 = 88.
Ta có : 88 = 1 x 88 = 2 x 44 = 4 x 22 = 8 x 11. 
Vậy tổng 2 số chia hết cho các số : 1 ; 2 ; 4 ; 8 ; 11 ; 22 ; 44 ; 88.
Bài 21 Tìm số có ba chữ số, biết số đó chia cho 2 dư 1, chia cho 5 dư 3 và chia hết cho 3, biết chữ số hàng trăm là 8.
Theo đề bài ta có: số đó có dạng , 0, a 0 
Để chia 2 dư 1 thì b = 1;3;5;7;9 ( 1)	
Để chia 5 dư 3 thì b = 3 hoặc 8 ( 2)
Từ (1) và (2) suy ra b = 3 
Số đó có dạng 
Để chia hết cho 3 thì (8 +a + 3) chia hết cho 3 hay (11 + a) chia hết cho 3 
Suy ra a = 1; 4; 7	
Vậy các số cần tìm là: 813; 843; 873	 
DẠNG TOÁN VỀ DÃY SỐ
Một số lưu ý khi giải toán về “dãy số”
	Trong bài toán về dãy số thường người ta không cho biết cả dãy số (vì dãy số có nhiều số không thể viết ra hết được) vì vậy, phải tìm ra được quy luật của dãy (mà có rất nhiều quy luật khác nhau) mới tìm được các số mà dãy số không cho biết. Đó là những quy luật của dãy số cách đều, dãy số không cách đều hoặc dựa vào dấu hiệu chia hết để tìm ra quy luật.Ở dạng 2: Muốn kiểm tra số A có thoả mãn quy luật của dãy đã cho hay không? Ta cần xem dãy số cho trước và số cần xác định có cùng tính chất hay không? (Có cùng chia hết cho một số nào đó hoặc có cùng số dư) thì số đó thuộc dãy đã cho.Ở dạng 3 và 4: Học sinh phải được tự tìm ra công thức tổng quát, vận dụng một cách thành thạo và biết biến đổi công thức để làm các bài toán khác. 
Ở dạng 9: Có các yêu cầu:
	+ Tìm tổng các số hạng của dãy.
	+ Tính nhanh tổng.
	Khi giải: Sau khi tìm ra quy luật của dãy, ta sắp xếp các số theo từng cặp sao cho có tổng đều bằng nhau, sau đó tìm số cặp rồi tìm tổng các số hạng của dãy. Chú ý: Khi tìm số cặp số mà còn dư một số hạng thì khi tìm tổng ta phải cộng số dư đó vào. 
	Nếu tính nhanh tổng của các phân số phải dựa vào tính chất của phân số.
	Ở dạng 10: Đó là dãy chữ khi giải phải dựa vào quy luật của dãy, sau đó có thể xem mỗi nhóm chữ có tất cả bao nhiêu chữ rồi đi tìm có tất cả bao nhiêu nhóm và đó chính là phần trả lời của bài toán. 
* Bài tập lự luyện:
Bài 1: Cho dãy số: 1, 4, 7, 10,
	a. Nêu quy luật của dãy.
	b. Số 31 có phải là số hạng của dãy không?
	c. Số 2009 có thuộc dãy này không? Vì sao?
Bài 2: Cho dãy số: 1004, 1010, 1016,, 2012.
	Hỏi số 1004 và 1760 có thuộc dãy số trên hay không?
Bài 3: Cho dãy số: 1, 7, 13, 19,,
	a. Nêu quy luật của dãy số rồi viết tiếp 3 số hạng tiếp theo.
	b. Trong 2 số 1999 và 2009 thì số nào thuộc dãy số? Vì sao?
Bài 4: Cho dãy số: 3, 8, 13, 18,
	Có số tự nhiên nào có chữ số tận cùng là 6 mà thuộc dãy số trên không?
Bài 5: Cho dãy số: 1, 3, 6, 10, 15,, 45, 55,
	a. Số 1997 có phải là số hạng của dãy số này hay không?
	b. Số 561 có phải là số hạng của dãy số này hay không? 
Dạng 3: Tìm số số hạng của dãy
	* Cách giải ở dạng này là:
Đối với dạng toán này, ta thường sử dụng phương pháp giải toán khoảng cách (toán trồng cây). Ta có công thức sau :
 Số các số hạng của dãy = số khoảng cách+ 1.
Đặc biệt, nếu quy luật của dãy là : Mỗi số hạng đứng sau bằng số hạng liền trước cộng với số không đổi d thì:
Số các số hạng của dãy = ( Số hạng lớn nhất – Số hạng nhỏ nhất ) : d + 1.
Các ví dụ:
Bài 1: Cho dãy số 11; 14; 17;.....;65; 68.
 Hãy xác định dãy số trên có bao nhiêu số hạng?
Lời giải : 
Ta có : 14 - 11= 3; 17 - 14 = 3;....
Vậy quy luật của dãy số đó là mỗi số hạng đứng liền sau bằng số hạng đứmg liền trước nó cộng với 3. Số các số hạng của dãy số đó là:
 ( 68 - 11 ) : 3 + 1 = 20 ( số hạng )
Bài 2: Cho dãy số: 2, 4, 6, 8, 10,, 1992
	Hãy xác định dãy số trên có bao nhiêu số hạng?
	Giải:
	Ta thấy:	4 – 2 = 2	;	8 – 6 = 2
	 6 – 4 = 2	;	
	Vậy, quy luật của dãy số là: Mỗi số hạng đứng sau bằng một số hạng đứng trước cộng với 2. Nói các khác: Đây là dãy số chẵn hoặc dãy số cách đều 2 đơn vị. 
	Dựa vào công thức trên:
	(Số hạng cuối – số hạng đầu) : khoảng cách + 1
	Ta có: Số các số hạng của dãy là:
	(1992 - 2) : 2 + 1 = 996 (số hạng).
Bài 3: Cho 1, 3, 5, 7,  là dãy số lẻ liên tiếp đầu tiên; hỏi 1981 là số hạng thứ bao nhiêu trong dãy số này? Giải thích cách tìm? 
(Đề thi học sinh giỏi bậc tiểu học 1980 – 1981)
	Giải: 
	Ta thấy:	
	Số hạng thứ nhất bằng:	1 = 1 + 2 x 0
	Số hạng thứ hai bằng: 	3 = 1 + 2 x 1
	Số hạng thứ ba bằng:	5 = 1 + 2 x 2
	Còn số hạng cuối cùng: 1981 = 1 + 2 x 990
	Vì vậy, số 1981 là số hạng thứ 991 trong dãy số đó.
Bài 4: Cho dãy số: 3, 18, 48, 93, 153,
	a. Tìm số hạng thứ 100 của dãy.
	b. Số 11703 là số hạng thứ bao nhiêu của dãy?
	Giải:
	a. 	Số hạng thứ nhất:	3 = 3 + 15 x 0
	Số hạng thứ hai:	18 = 3 + 15 x 1
	Số hạng thứ ba:	48 = 3 + 15 x 1 + 15 x 2
	Số hạng thứ tư:	93 = 3 + 15 x 1 + 15 X 2 + 15 x 3
	Số hạng thứ năm:	153 = 3 + 15 x 1 + 15 x 2 + 15 x 3 + 15 x 4
	Số hạng thứ n:	3 + 15 x1 + 15 x 2 +15 x 3 +  + 15 x (n - 1)
	Vậy số hạng thứ 100 của dãy là:
	3 + 15 x 1 + 15 x 2 +  + 15 x (100 - 1)
	= 3 + 15 x (1 + 2 + 3 +  + 99) (Đưa về một số nhân với một tổng.
	= 3 + 15 x (1 + 99) x 99 : 2 = 74253
	b. Gọi số 11703 là số hạng thứ n của dãy:
	Theo quy luật ở phần a ta có:
	3 + 15 x 1 + 15 x 2 + 15 x 3 +  x (n – 1) = 11703
	3 + 15 x (1 + 2 + 3 + + ( n – 1))	 = 11703
	3 + 15 x (1 + n – 1) x (n – 1) : 2	 = 11703
	15 x n x (n – 1) = (11703 – 3) x 2	 = 23400
	 n x (n – 1) = 23400 : 15	 = 1560
Nhận xét: Số 1560 là tích của hai số tự nhiên liên tiếp 39 và 40 (39 x 40 = 1560)
	Vậy, n = 40, số 11703 là số hạng thứ 40 của dãy.
Bài 5: Trong các số có ba chữ số, có bao nhiêu số chia hết cho 4?
Lời giải: 
 Ta nhận xét : Số nhỏ nhất có ba chữ số chia hết cho 4 là 100 và số lớn nhất có ba chữ số chia hết cho 4 là 996. Như vậy các số có ba chữ số chia hết cho 4 lập thành một dãy số có số hạng nhỏ nhất là 100, số hạng lớn nhất là 996 và mỗi số hạng của dãy ( kể từ số hạng thứ hai ) bằng số hạng đứng liền trước cộng với 4. 
 Vậy số các số có ba chữ số chia hết cho 4 là :
 ( 996 – 100 ) : 4 = 225 ( số )
* Bài tập tự luyện:
Bài 1: Cho dãy số: 3, 8, 13, 23, ,2008
	Tìm xem dãy số có bao nhiêu số hạng ?
Bài 2: Tìm số số hạng của các dãy số sau: 
	a. 1, 4, 7, 10, ,1999.
	b. 1,1 ; 2,2 ; 3,3 ; ... ; 108,9 ; 110,0.
Bài 3: Xét dãy số: 100, 101, , 789.
	Dãy này có bao nhiêu số hạng?
Bài 4: Có bao nhiêu số khi chia cho 4 thì dư 1 mà nhỏ hơn 2010 ?
Bài 5: Người ta trồng cây hai bên đường của một đoạn đường quốc lộ dài 21km. Hỏi phải dùng bao nhiêu cây để đủ trồng trên đoạn đường đó ? Biết rằng cây nọ trồng cách cây kia 5m. 
Dạng 4: Tìm số hạng thứ n của dãy số
Bài toán 1: Cho dãy số: 1, 3, 5, 7,............Hỏi số hạng thứ 100 của dãy số là số nào 
Giải:
Số khoảng cách từ số đầu đến số hạng thứ 100 là:
 98 - 1 = 99
Mỗi khoảng cách là
 3 - 1 = 5 - 3 = 2
Số hạng thứ 100 là
 1 + 99 ´ 2 = 199
Công thức tổng quát:
 Số hạng thứ n = số đầu + khoảng cách ´ (Số số hạng - 1)
Bài toán 2: Tìm số hạng thứ 100 của các dãy số được viết theo quy luật:
3, 8, 15, 24, 35, (1)
3, 24, 63, 120, 195, (2) 
1, 3, 6, 10, 15,. (3)
Giải: a) Dãy (1) có thể viết dưới dạng: 1x3, 2x4, 3x5, 4x6, 5x7,
	Mỗi số hạng của dãy (1) là tích của hai thừa số, thừa số thứ hai lớn hơn thừa số thứ nhất 2 đơn vị. Các thừa số thứ nhất làm thành một dãy: 1, 2, 3, 4, 5, ; Dãy này có số hạng thứ 100 là 100.
Số hạng thứ 100 của dãy (1) bằng: 100x102 = 10200.
	b) Dãy (2) có thể viết dưới dạng: 1x3, 4x6, 7x9, 10x12, 13x15,
Mỗi số hạng của dãy (2) là tích của hai thừa số, thừa số thứ hai lớn hơn thừa số thứ nhất 2 đơn vị. Các thừa số thứ nhất làm thành một dãy: 1, 4, 7, 10, 13, ; Số hạng thứ 100 của dãy 1, 4, 7, 10, 13, là: 1 + (100 – 1 ) x 3 = 298.
Số hạng thứ 100 của dãy (2) bằng: 298 x 300 = 89400.
c) Dãy (3) có thể viết dưới dạng: 
 ...
Số hạng thứ 100 của dãy (3) bằng: 	
* Bài tập tự luyện:
Bài 1: Cho dãy số : 101, 104, 107, 110, ......
Tìm số hạng thứ 1998 của dãy số đó.
Bài 2: Cho dãy số : 5, 8, 11, 14, ......
a.Tìm số hạng thứ 200 của dãy số.
b. Nếu cứ viết tiếp thì các số : 1000 ; 2009 ; 5000 có là số hạng của dãy không ? Tại sao.
Bài 3: Một bạn học sinh viết liên tiếp các số tự nhiên mà khi chia cho 3 thì dư 2 bát đầu từ số 5 thành dãy số. Viết đến số hạng thứ 100 thì phát hiện đã viết sai. Hỏi bạn đó đã viết sai số nào ?
Dạng 5: Tìm số chữ số của dãy khi biết số số hạng
Bài toán 1: Cho dãy số: 1, 2, 3,.......150. Hỏi để viết dãy số này người ta phải dùng bao nhiêu chữ số 
Giải:
Dãy số đã cho có : ( 9 - 1) : 1 + 1 = 9 số có 1 chữ số. 
Có ( 99 - 10 ) : 1 + 1 = 90 số có 2 chữ số
 Có ( 150 - 100) : 1 + 1 = 51 số có 3 chữ số.
Vậy số chữ số cần dùng là :
 9 ´ 1 + 90 ´ 2 + 51 ´ 3 = 342 chữ số
Bài toán 2: Một quyển sách có 234 trang. Hỏi để đánh số trang quyển sách đó người ta phải dùng bao nhiêu chữ số. 
Giải:
Để đánh số trang quyển sách đó người ta phải viết liên tiếp các số tự nhiên từ 1 đến 234 thành dãy số. Dãy số này có 
 ( 9 - 1) : 1 + 1 = 9 số có 1 chữ số
Có: ( 99 - 10) : 1 + 1 = 90 số có 2 chữ số
Có: ( 234 - 100) : 1 + 1 = 135 số có 3 chữ số
Vậy người ta phải dùng số chữ số là:
9 ´ 1 + 90 ´ 2 + 135 ´ 3 = 594 chữ số
* Bài tập tự luyện:
Bài 1: Một bạn học sinh viết liên tiếp các số tự nhiên từ 101 đến 2009 thành 1 số rất lớn. Hỏi số đó có bao nhiêu chữ số
Bài 2: Trường Tiểu học Thành Công có 987 học sinh. Hỏi để ghi số thứ tự học sinh trường đó người ta phải dùng bao nhiêu chữ số
Bài 3: Cần bao nhiêu chữ số để đánh số trang của một cuốn sách có tất cả là:
a.752 trang.
b.1251 trang.
Dạng 6: Tìm số số hạng khi biết số chữ số
Bài toán 1: Để đánh số trang 1 quyển sách người ta dùng hết 435 chữ số. Hỏi quyển sách đó có bao nhiêu trang?
Giải:
Để đánh số trang quyển sách đó, người ta phải viết liên tiếp các số tự nhiên bắt đầu từ 1 thành dãy số. Dãy số này có
 9 số có 1 chữ số
 có 90 số có 2 chữ số
Để viết các số này cần số chữ số là
 9 ´ 1 + 90 ´ 2 = 189 chữ số
Số chữ số còn lại là:
- 189 = 246 chữ số
Số chữ số còn lại này dùng để viết tiếp các số có 3 chữ số bắt đầu từ 100. Ta viết được 
246 : 3 = 82 số
Số trang quyển sách đó là
 99 + 82 = 181 ( trang)
Bài toán 2: 
Để đánh số trang một cuốn sách người ta phải dùng tất cả 600 chữ số. Hỏi quyển sách đó có bao nhiêu trang? 
Giải: 99 trang đầu cần dùng 9x1 + 90x2 = 189 chữ số.
 999 trang đầu cần dùng: 9x1 + 90x2 + 900x3 = 2889 chữ số 
 Vì: 189 < 600 < 2889 nên trang cuối cùng phải có 3 chữ số. Số chữ số để đánh số các trang có 3 chữ số la: 600 - 189 = 411 (chữ số) 
 Số trang có 3 chữ số là 411: 3 = 137 trang.
 Vậy quyển sách có tất cả là: 99 + 137 = 236 trang.
Bài toán 3: Để ghi thứ tự các nhà trên một đường phố, người ta dùng các số chẵn 2, 4, 6, 8 . . . để ghi các nhà ở dãy phải và các số lẻ 1, 3, 5, 7 . . . để ghi các nhà ở dãy trái của đường phố đó. Hỏi số nhà cuối cùng của dãy chẵn trên đường phố đó là bao nhiêu, biết rằng khi đánh thứ tự các nhà của dãy này, người ta đã dùng 367 lượt chữ số cả thảy. 
Giải:
Số nhà có số thứ tự ghi bằng 1 chữ số chẵn là: (8 - 2) : 2 + 1 = 4 (nhà)