Môn Toán 9 - Phần hình học định kì

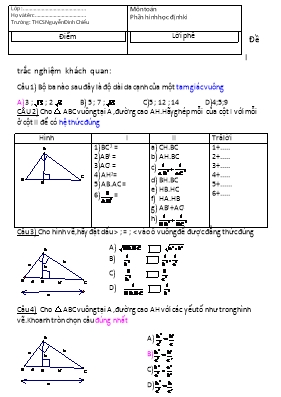
Lớp :.
Họ và tên:.
Trường : THCS Nguyễn Đình Chiểu
Môn toán
Phần hình học định kì
Điểm
Lời phê
Đề 
I trắc nghiệm khách quan:
Câu 1) Bộ ba nào sau đây là độ dài da cạnh của một tam giác vuông
A) 3 ; ; 2
B) 5 ; 7 ;
C)5 ; 12 ; 14
D)4;5;9
CÂU 2) Cho r ABC vuông tại A ,đường cao AH.Hãy ghép mỗi ‎ của cột I với mỗi ‎ ở cột II để có hệ thức đúng
 Hình
 I
 II
Trả lời
1) BC2 =
2)AB2 =
3)AC2 =
4) AH2=
5) AB.AC =
6)=
a) CH.BC
b) AH.BC
c)
d) BH.BC
e) HB.HC
f) HA.HB
g) AB2+AC2
h)
1+.....
2+.....
3+.....
4+.....
5+......
6+.....
Câu 3) Cho hình vẽ,hãy đặt dấu > ; = ; < vào ô vuông để được đẳng thức đúng
A) 
B) 
C) 
D) 
Câu 4) Cho r ABC vuông tại A ,đường cao AH với các yếu tố như trong hình vẽ.Khoanh tròn chọn câu đúng nhất 
A) 
B)
C)
D)
Câu 5) Cho r ABC vuông tại A ,đường cao AH với các yếu tố như trong hình vẽ.
 Chọn câu SAI
A) 
B) 
C) 
D) 
Câu 6) rCHA có CA=5 ;AH= 12 ;CH=13 ,khi đó:
A) =900
B) < 900
C) >900
D) =900
Câu 7)r CAM có CA= 5; AM=7;CM=8,khi đó:
A) =900
B) < 900
C) > 900
D)=900
Câu 8)r NHO có NH =5 ; OH=7 ; ON = 9, khi đó :
A) =900
B) < 900
C) > 900
D) =900
Câu 9) rTAO có bình phương cạnh huyền bằng 289 và diện tích là 60.Độ dài hai cạnh góc vuông là
A) 12 và 13
B) 8 và 15
C) 12 và 17
D)10va2 12
Câu 10) Cho r ABC vuông tại A.Trong các phát biểu sau đây,phát biểu nào SAI ?
A) AB2=BC2-AC2
B) BC2=AB2+AC2
C) AC2=BC2-AB2
D) AB2=AC2 –BC2
Câu 11) Nếu r ABC có AB2=AC2 –BC2 thì 
A) Tam giác đó vuông tại A
B)Tam giác đó vuông tại B
C)Tam giác đó vuông tại C
D)Tam giác đó vuông cântại A
Câu 12)Cho r ABC vuông tại A ,đường cao AH với các yếu tố như trong hình vẽ.
 Chọn câu đúng
A) AH2=BH2+CH2
B) AH=HB.HC
C) AH2=AC2- AB2
D) AH= 
Câu 13)Cho r ABC vuông tại A ,đường cao AH với các yếu tố như trong hình vẽ.
 Chọn câu đúng
A) AB.AH=AC.BC
B) BC.AH= AB2+AC2
C) AC.AH=AB.BC
D) BC=
Câu 14)Cho r ABC vuông tại A ,đường cao AH với các yếu tố như trong hình vẽ.
 Chọn câu SAI
A) AB2=BH.BC
B) AC2=CH.CB
C) BC=
D) AH.BC=AB.AC
Câu 15)Chor ABC vuông tại A ,có AC= 21 cm ; AB =20 cm; độ dài đường cao AH bằng
A) 17 cm
B) 30 cm
C) 29 cm
D)cm
Câu 16) Chor ABC vuông tại B ,có BC= 8 cm ; BA = cm; độ dài đường cao BD bằng
A) 2 cm
B) 4 cm
C)3 cm
D) 12 cm
Câu 17) Bạn nào nói đúng ?
A)Bạn Xuân nói: Có tam giác vuông có độ dài3 cạnh là 3 số tự nhiên lẻ liên tiếp
B)Bạn Hạ nói: Có tam giác vuông có độ dài3 cạnh là 3 số tự nhiên chẵn liên tiếp
C)Bạn Thu nói: Không có tam giác vuông nào có số đo chu vi lớn gấp đôi số đo diện tích của nó
D)Bạn Đông nói: Không có tam giác vuông nào có độ dài 3 cạnh là số vô tỉ
Câu 18)Trong các khẳng định sau khẳng định nào đúng?
r ABC có đường cao AH
A)Nếu AB2=BH.HC thì r ABC vuông tại A
B)Nếu AH2=HB.HC thì r ABC vuông tại A
C)Nếu AB.AC=AH.BC thì r ABC vuông tại A
D)Nếu thì r ABC vuông tại A
Câu 19) Dựa vào hình vẽ ,ta có
x =9,6 và y = 5, 4
x =6 và y = 8
x=4,5 và y=6,9
x=5,4 và y=9,6
Câu 20) Dựa vào hình vẽ ,ta có
A) x = và y =2
B) x=2 và y =2
 C)x=2 và y =2
 D) x= 2 và y=2
Câu 21) Dựa vào hình vẽ ,ta có
A) x= 5 và y= 10
B) x= 4,8 và y =10
C) x =4 và y =12
D) x =7 và y=10
Câu 22) Dựa vào hình vẽ ,ta có
A) x=20cm; y=30 cm
B) x=16 cm; y= 25 cm
C) x= 20 cm ; y=35 cm
D) x= 18 cm ; y =32 cm
Câu 23) Dựa vào hình vẽ ,ta có
A) x =2 ; y = 4
B) x = ; y =
C) x = 2 ; y = 2
D) x = 4 ; y =
Câu 24;25) Dựa vào hình vẽ ,ta có
Câu 24) Độ dài cạnh AH bằng
A) 5 B) 6 C) 6,5 D) 6,9
Câu 25)Độ dài cạnh AC bằng:
A) 12 B) 13 C) D) 3 
Câu 26) rABC có đường cao AH, AB =9cm; AC= 12 cm; BC =15 cm,câu nào sau đây SAI ?
A)rABC vuông tại A
B) AH= 7,5 cm
C) BH=5,4 cm
HC=9,6 cm
Câu 27) Dựa vào hình vẽ ,ta có
A) x=2 ; y =
B)x=4;y=2
C)x=4;y=2
D)x=;y=
Câu 28) Dựa vào hình vẽ , độ dài cạnh AC là
A)40 B) 50
C)30 D)45
Câu 29)Đướng cao của một tam giác vuông chia cạnh huyền thành hai đoạn thẳng có độ dài 1 và 2.Độ dài hai cạnh góc vuông là:
A) và 
B) 5 và 8
C) 3 và 6
D)3 và 4
Câu 30*)rABC vuông tại A có ; đường cao AH=15 cm.Khi đó độ dài CH là
A) 20 cm
B)15 cm
C)10cm
D)25 cm
Câu 31*) ChorPQR vuông tại P có đường cao PH =24 cm và .
;khi đó độ dài QR bằng
A) 25 cm
B) 50 cm
C) 48 cm
D) 20 cm
Câu 32*)rABC vuông tại A có ; BC=39cm.Khi đó độ dài cạnh AB và AC là là
A) AB=15cm; AC=36cm
B)AB=10 cm và AC=24cm
C)AB=6cm và AC=14,4 cm
D)AB=5cm vàAC=12 cm
Câu 33*)Một tam giác vuông có cạnh góc vuông lớn dài gấp 3 lần cạnh góc vuông nhỏ và diện tích là 24 cm2.Khi đó độ dài cạnh huyền là:
A) 12 cm
B) 13 cm
C) 4 cm
D) 4cm
Câu 34) Dựa vào hình vẽ; x bằng:
A) 6 cm
B) 8 cm
C) 9 cm
D) 10 cm
Câu 35) Cho tam giác vuông có hai góc nhọn α và ,Biểu thức nào sau đây không đúng ?
A)sinα = cos
B)sin2α+cos2=1
C)cotg α= tg
D)tg α= cotg
Câu 36) Cho α=350 và =550.Chọn đáp án sai
A) sin α= sin
B) sin α= cos
C) tg α= cotg
D)cos α= sin
Câu 37=>39)Chọn câu đúng. Cho tgα = . Khi đó
(37) cotg α nhận kết quả bằng
A) 1
B) 2
C) 
D) cả 3 câu trên đều sai
(38) cos α nhận kết quả bằng
A) 
B)
C) 1
D)
(39) sinα nhận kết quả bằng
A)
B)
C)1
D)
Câu 40=>42)Chọn câu đúng. Cho cos α =.Khi đó
(40) sin α nhận kết quả bẳng
A) 
B) 
C)
D)
(41)tg α nhận kết quả bẳng
A)
B)
C)
D)3
(42)cotg α nhận kết quả bẳng
A)
B)
C)2
D)
Câu 43)Đặt dấu” > , < , = “ vào ô vuông
Sin 510
Sin 250
Cos 180
Cos 280
 Sin 250
Cos 250
 Tg 200
Cotg 300
 Sin 300
Tg 450
 Cos 300
Cotg 450
Tg 460
Sin 460
Cotg 470
Cos 470
Câu 44)Dựa vào hình vẽ,theo định nghĩa TSLG của góc nhọn ta có các hệ thức
Sin A= 
 Cos A=
Tg A=
Cotg A =
Câu 45)Dựa vào hình vẽ câu 44).Theo hệ thức liên hệ cạnh và góc trong rvuông ABC ta có
1)AC=sin.....
2) AC= cos.....
3) AC=tg.....
4) AC=cotg.....
 Câu 46)Trong hình vẽ, sin Q bằng
A) B) 
C) D) 
 Câu 47) Nếu sin α= thì cosα bằng
A) 
B) 
C) 
D) 
 Câu 48) Nếu tgα = thì cotgα bằng
A) 1
B) 
C) 
D) 
Câu 50: Cho DABC vuông tại A có đường cao AH . Giá trị của AH bằng bao nhiêu khi BH = 9, HC = 25.
A. 	B. 	C. 	D. 
Câu 51: Cho DABC vuông tại A , có . Khi đó các tỉ số lượng giác của góc 550 là 
Câu 52: Cho tam giác ABC vuông tại A , có đường cao AH =8, HC = 10. Khi đó HB, AB bằng bao nhiêu ?
Câu 53: Giá trị của biểu thức: A = cos 600 +sin 300 – sin 100 +cos 800 + tg 450 bằng
A. 	B. 	C. 	D. 
Câu 54: Cho tam giác ABC vuông tại A có AB = 20, . Khi đó và BC = 40. Đúng hay sai? (Đánh x vào ô vuông để có kết quả đúng).
 Đúng Sai
Câu 55: Cho tam ABC vuông tại A có AC = 8, . Khi đó AB bằng bao nhiêu ?
Câu 56: Cho tam giác ABC vuông tại A có đường cao AH, BH = 9, CH = 16. Khi đó AB và AC bằng:
A. AB = 15, AC = 10	B. AB = 12, AC = 20
C. AB = 15, AC = 20	D. Một kết quả khác.
Câu 57: Cho thì tgA bằng:
A. 	B. 	C. 	D. 
Câu 58: Một cái thang dài 4m , đặt dựa vào tường , góc giãư thang và mặt đất là 600 . Khi đó khoảng cách giữa chân thang đến tường bằng:
A. (m)	B. 2 (m)	C. (m)	D. (m)
Câu 59: Một tam giác ABC có góc B bằng 600 , AB = 6 cm, BC = 4 cm. Khi đó AC bằng bao nhiêu ?
Câu 60: Tam giác ABC vuông tại A có đường cao AH, BH = 9 và CH = 16. Khi đó AB, AC, AH bằng bao nhiêu ?
Câu 61: Tam giác ABC vuông tại A có đường cao AH = 8, HC = 10 . Khi đó diện tích tam ABC bằng:
A. 80	B. 	C. 	D. một kết quả khác.
Câu 62: Dãy tỉ số sau sắp xếp đúng hay sai:
Cotg 620 < tg 320 < tg 440 < cotg 250 < cotg 180 
(Đánh x vào ô vuông để có kết quả đúng ). 	
 Đúng Sai
Câu 63: Cho , thì tgA bằng:
A. 	B. 	C. 	D. 
Câu 64: Một tam giác ABC có , AB = 6 cm, BC = 4 cm . Khi đó AC bằng: 
A. (cm)	B. (cm) 	C. (cm) 	D. (cm)
Câu 65: Tam giác DEF có ED = 7, . Khi đó EF bằng bao nhiêu ( tính gần đúng với một chữ số thập phân ) ?
Câu 66: Tam giác ABC vuông tại A có AB = 3, AC = 4 , đường cao AH và trung tuyến AM. Khi đó HM bằng:
A. 	B. 	C. 	D. 
Câu 67: Rút gọn biểu thức bằng:
A. 1	B. 	C. 	D. 2
Cau 68 cho tam giác ABC co AB=9;AC =13 góc C=B=30 TÍNH s tan giác ABC
II bài tập
Cho tam giác ABC vuông tại A có AB = 3cm, BC = 5cm. AH là đường cao. Tính BH, CH, AC và AH.
	ĐS: , , , .
Cho tam giác ABC vuông tại A có AC = 10cm, AB = 8cm. AH là đường cao. Tính BC, BH, CH, AH.
	ĐS: 
Cho tam giác ABC vuông tại A có BC = 12cm. Tính chiều dài hai cạnh góc vuông biết .
	ĐS: , .
Cho tam giác ABC vuông tại A có đường cao AH. Biết BH = 10cm, CH = 42 cm. Tính BC, AH, AB và AC.
	ĐS: , , , .
Hình thang cân ABCD có đáy lớn AB = 30cm, đáy nhỏ CD = 10cm và góc A là .
	a) Tính cạnh BC.	b) Gọi M, N lần lượt là trung điểm AB và CD. Tính MN.
	ĐS: 
Cho tứ giác lồi ABCD có AB = AC = AD = 10cm, góc B bằng và góc A là .
	a) Tính đường chéo BD.	b) Tính các khoảng cách BH và DK từ B và D đến AC.
	c) Tính HK.	d) Vẽ BE ^ DC kéo dài. Tính BE, CE và DC.
	ĐS: 
Cho đoạn thẳng AB = 2a. Từ trung điểm O của AB vẽ tia Ox ^ AB. Trên Ox, lấy điểm D sao cho . Từ B kẽ BC vuông góc với đường thẳng AD.
	a) Tính AD, AC và BC theo a.
	b) Kéo dài DO một đoạn OE = a. Chứng minh bốn điểm A, B, C và E cùng nằm trên một đường tròn.
	ĐS: 
Cho tam giác nhọn ABC có hai đường cao BD và CE cắt nhau tại H. Trên HB và HC lần lượt lấy các điểm M, N sao cho . Chứng minh: AM = AN.
	HD: DABD # DACE Þ . 
Cho tam giác ABC vuông tại A, đường cao AH. Biết và AH = 420. Tính chu vi tam giác ABC.
	ĐS: . Đặt . Từ AH.BC = AB.AC Þ .
 Cho hình thang ABCD vuông góc tại A và D. Hai đường chéo vuông góc với nhau tại O. Biết , tính diện tích hình thang ABCD.
	ĐS: . Tính được: OB = 4, OD = 9, OC = 13,5.
 Bài 11 Cho tam giác ABC vuông tại A, đường cao AH. Biết BH = 64cm và CH = 81cm. Tính các cạnh và góc tam giác ABC.
	ĐS: 
Bài 12 Cho tam giác ABC vuông tại A. Tìm các tỉ số lượng giác của góc B khi:
	a) BC = 5cm, AB = 3cm.	b) BC = 13 cm, AC = 12 cm.	c) AC= 4cm, AB=3cm.
	ĐS: a) ; 
Bài 13 Cho tam giác ABC vuông tại A, có AB = 10cm và AC = 15cm.
	a) Tính góc B.	b) Phân giác trong góc B cắt AC tại I. Tính AI.
	c) Vẽ AH ^ BI tại H. Tính AH.
	ĐS: 
Tính giá trị các biểu thức sau:
	a) .
	b) .
	c) 	d) 
	e) 	f) 
	ĐS: a) 	b) 	c) 	d) 0	e) 2	f) 0.
Cho biết một tỉ số lượng giác của góc nhọn a, tính các tỉ số lượng giác còn lại của a: 
	a) 	b) 	c) 	d) 
	ĐS: a) 	b) 
Cho góc nhọn a. Biết . Tính .
	ĐS: .
Cho tam giác ABC vuông tại C. Biết . Tính .
	ĐS: .
Rút gọn các biểu thức sau:
	a) 	b) 	c) 
	d) 	e) 	f) 
	ĐS: a) 	b) 2	c) 	d) 1	e) 	f) 1.
Chứng minh các hệ thức sau:
	a) 	b) 
	ĐS: 
Cho tam giác nhọn ABC. Gọi a, b, c lần lượt là độ dài các cạnh đối diện với các đỉnh A, B, C.
	a) Chứng minh:	.
	b) Có thể xảy ra đẳng thức không?
	ĐS: a) Vẽ đường cao AH. Chú ý: .	b) không.
Giải tam giác vuông ABC, biết và:
	a) 	b) 
	ĐS: a) 	b) .
Cho tam giác ABC có . Tính diện tích tam giác ABC.
	ĐS: . Vẽ đường cao AH. Tính AH, HB, HC.
Cho tứ giác ABCD có . Tính diện tích tứ giác.
	ĐS: . Vẽ BH ^ CD. Tính DH, BH, CH.
Cho tứ giác ABCD có các đường chéo cắt nhau tại O. Cho biết , . Tính diện tích tứ giác ABCD.
	ĐS: . Vẽ AH ^ BD, CK ^ BD. Chú ý: .
Chứng minh rằng:
	a) Diện tích của một tam giác bằng nửa tích của hai cạnh nhân với sin của góc nhọn tạo bởi các đường thẳng chứa hai cạnh ấy.
	b) Diện tích của một hình bình hành bằng tích của hai cạnh kề nhân với sin của góc nhọn tạo bởi các đường thẳng chứa hai cạnh ấy.
	ĐS: a) Gọi a là góc nhọn tạo bởi hai đường thẳng AB, AC. Vẽ đường cao CH. 
Cho tam giác ABC có AB = 21m, AC = 28m, BC = 35m.
	a) Chứng minh tam giác ABC vuông.	b) Tính .
	ĐS: 
Cho tam giác ABC vuông tại A, đường cao AH, đường phân giác AD. Cho biết HB = 112, HC = 63.
	a) Tính độ dài AH.	b) Tính độ dài AD.
	ĐS: a) AH = 84	b) .
Cho tam giác ABC vuông tại A, đường cao AH. Biết AH = 5, CH = 6.
	a) Tính AB, AC, BC, BH.	b) Tính diện tích tam giác ABC.
	ĐS: a) , , 	b) .
Cho tam giác ABC vuông tại A, đường cao AH. Biết AH = 16, BH = 25.
	a) Tính AB, AC, BC, CH.	b) Tính diện tích tam giác ABC.
	ĐS: 
Cho hình thang ABCD có và hai đường chéo vuông góc với nhau tại O.
	a) Chứng minh hình thang này có chiều cao bằng trung bình nhân của hai đáy.
	b) Cho AB = 9, CD = 16. Tính diện tích hình thang ABCD.
	c) Tính độ dài các đoạn thẳng OA, OB, OC, OD.
	ĐS: a) Vẽ AE // BD Þ AB = ED và AE ^ AC. 	b) S = 150	
	c) .
Tính diện tích hình thang ABCD (AB // CD), biết AB = 10, CD = 27, AC = 12, BD = 35.
	ĐS: S = 210. Vẽ BE // AC (E Î CD) Þ .
Cho biết chu vi của một tam giác bằng 120cm. Độ dài các cạnh tỉ lệ với 8, 15, 17.
	a) Chứng minh rằng tam giác đó là một tam giác vuông.
	b) Tính khoảng cách từ giao điểm ba đường phân giác đến mỗi cạnh.
	ĐS: a) Tính được AB = 24cm, AC = 45cm, BC = 51cm Þ DABC vuông tại A.
	b) r = 9cm. Gọi O là giao điểm ba đường phân giác. .
Cho tam giác ABC cân tại A, đường cao AH. Biết . Tinh chu vi DABC
	ĐS: .
 Cho ABC vuông tại A, AB = a, AC = 3a. Trên cạnh AC lấy các điểm D, E sao cho AD = DE = EC.
	a) Chứng minh .	b) Chứng minh đồng dạng CDB.
	c) Tính tổng .
	ĐS: a) 	c) .
 Cho hình thang ABCD có hai cạnh bên AD và BC bằng nhau, đường chéo AC vuông góc với cạnh bên BC. Biết AD = 5a, AC = 12a.
	a) Tính .	b) Tính diện tích hình thang ABCD.
	ĐS: a) 	b) 
 Cho tam giác ABC vuông tại A, đường cao AH. Gọi D là điểm đối xứng với A qua điểm B. Trên tia đối của tia HA lấy điểm E sao cho HE = 2HA. Gọi I là hình chiếu của D trên HE.
	a) Tính AB, AC, HC, biết AH = 4cm, HB = 3cm.	b) Tính .
	c) Chứng minh .	d) Chứng minh: .
	ĐS: a) , , 	b) 
	d) .
Cho tam giác ABC vuông tại A (AB < AC), đường cao AH. Đặt BC = a, CA = b, AB = c, AH = h. Chứng minh rằng tam giác có các cạnh là một tam giác vuông.
	ĐS: Chứng minh .
Cho tam giác nhọn ABC, diện tích bằng 1. Vẽ ba đường cao AD, BE, CF. Chứng minh rằng:
	a) .	b) .
	ĐS: a) Chứng minh 	b) 
Cho ABC vuông tại A có . Tính các tỉ số lượng giác của góc B và C.
	ĐS: ; ; ; .
 Cho tam giác ABC có ba đường cao AM, BN, CL. Chứng minh:
	a) DANL #DABC	b) 
	ĐS: 
 Cho tam giác ABC vuông tại A có , BC = 4cm.
	a) Kẻ đường cao AH, đường trung tuyến AM. Tính , AH, AM, HM, HC.
	b) Chứng minh rằng: .
	ĐS: a) ; ; ; ; 
	b) .
 Cho tam giác ABC cân tại A, có , BC = 1cm. Kẻ phân giác CD. Gọi H là hình chiếu vuông góc của D trên AC.
	a) Tính AD, DC.	b) Kẻ CK BD. Giải tam giác BKC.
	c) Chứng minh rằng .
	ĐS: 
 Cho tam giác ABC có AB = 1, , . Trên cạnh BC lấy điểm E sao cho BE = 1. Vẽ ED // AD (D thuộc AC). Đường thẳng qua A vuông góc với AC cắt BC tại F. Gọi H là hình chiếu của A trên cạnh BC.
	a) Chứng minh rằng tam giác ABE đều. Tính AH.	
	b) Chứng minh .
	c) Tính các tỉ số lượng giác của góc AED và góc AEF.	
	d) Chứng minh . Từ đó suy ra AD = AF.
	e) Chứng minh rằng .
	ĐS: 
 Giải tam giác ABC, biết:
	a) 	b) .
	c) Trung tuyến ứng với cạnh huyền , đường cao AH = 4.
	d) Trung tuyến ứng với cạnh huyền , một góc nhọn bằng .
	ĐS: 
 Cho tam giác ABC vuông tại A, đường cao AH, AB = 3cm, BC = 6cm. Gọi E, F lần lượt là hình chiếu của H trên cạnh AB và AC.
	a) Giải tam giác vuông ABC. 	b) Tính độ dài AH và chứng minh: EF = AH.
	c) Tính: EA.EB + AF.FC.
	ĐS: a) , , 	b) 	c) .
Cho tam giác ABC vuông tại A có AB = 3cm, BC = 5cm. AH là đường cao. Tính BH, CH, AC và AH.
ĐS: ,
 , , .
Cho tam giác ABC vuông tại A có AC = 10cm, AB = 8cm. AH là đường cao. Tính BC, BH, CH, AH.
ĐS: 
Cho tam giác ABC vuông tại A có BC = 12cm. Tính chiều dài hai cạnh góc vuông biết .
ĐS:
 , .
Cho tam giác ABC vuông tại A có đường cao AH. Biết BH = 10cm, CH = 42 cm. Tính BC, AH, AB và AC.
ĐS:
 , , , .
Hình thang cân ABCD có đáy lớn AB = 30cm, đáy nhỏ CD = 10cm và góc A là .
a) Tính cạnh BC. b) Gọi M, N lần lượt là trung điểm AB và CD. Tính MN.
ĐS: 
Cho tứ giác lồi ABCD có AB = AC = AD = 10cm, góc B bằng và góc A là .
a) Tính đường chéo BD. b) Tính các khoảng cách BH và DK từ B và D đến AC.
c) Tính HK. d) Vẽ BE ( DC kéo dài. Tính BE, CE và DC.
ĐS: 
Cho đoạn thẳng AB = 2a. Từ trung điểm O của AB vẽ tia Ox ( AB. Trên Ox, lấy điểm D sao cho . Từ B kẽ BC vuông góc với đường thẳng AD.
a) Tính AD, AC và BC theo a.
b) Kéo dài DO một đoạn OE = a. Chứng minh bốn điểm A, B, C và E cùng nằm trên một đường tròn.
ĐS:  . 
Cho tam giác ABC vuông tại A, đường cao AH. Biết và AH = 420. Tính chu vi tam giác ABC.
ĐS: . 
Cho hình thang ABCD vuông góc tại A và D. Hai đường chéo vuông góc với nhau tại O. Biết , tính diện tích hình thang ABCD.
Bài tập 1: Cho tam giác ABC vuông tại A, đường cao AH, biết AB = 4cm, AC = 7,5cm, tính
HB,HC.
Bài tập 2: Cho tam giác ABC vuông tại A, đường cao AH .
a. Biết AH = 6cm, BH = 4,5cm, Tính AB, AC, BC,HC
b. Biết AB = 6cm, BH = 3cm, Tính AH,AC,CH
Bài tập 3: Cho tam giác vuông ABC vuông tại A, đường cao AH, tính diện tích tam giác ABC,
biết AH = 12cm, BH = 9cm
Bài tập 4: Cho tam giác ABC, biết BC = 7,5 cm, CA= 4,5cm, AB= 6cm
a. Tam giác ABC là tam giác gì? Tính đường cao AH của tam giác ABC ;
b. Tính độ dài các đoạn thẳng BH, CH
Bài tập 5: Cho tam giác vuông với các cạnh góc vuông lần lượt là 7 và 24. Kẻ đường cao ứng với cạnh huyền. Tính độ dài đường cao và các đoạn thẳng mà đường cao đó chia ra trên cạnh huyền.
Bài tập 6: Cho một tam giác vuông, biết tỉ số hai cạnh góc vuông là 5/12
, cạnh huyền là 26cm.
Tính độ dài các cạnh góc vuông và hình chiếu của cạnh góc vuông trên cạnh huyền
Bài tập 7: Cho tam giác ABC vuông ở A. Biết AB=5 ,AC=7
đường cao AH = 15cm. Tính HB, HC.
Bài tập 8: Cho hình thang cân ABCD (AB// CD), biết AB=26cm, AD =10cm và đường chéo AC vuông góc với cạnh bên BC. Tính diện tích của hình thang ABCD.
Bài tập 9: Cho tam giác ABC vuông ở A, AB = 12cm, AC =16cm, phân giác AD, đường cao AH.
Tính độ dài các đoạn thẳng HB,HD,HC .
Bài tập 10: Cho tam giác ABC vuông ở A, phân giác AD đường cao AH. Biết BD = 15cm,CD = 20cm.
Tính độ dài các đoạn thẳng BH,HC
Bài tập 23: Tam giác ABC vuông tại A, đường cao AH. Biết HB = 25cm, HC = 64cm. Tính BC
Bài tập 25: Một hình bình hành có hai cạnh là 10cm và 12cm, góc tạo bởi hai cạnh đó bằng 150
Tính diện tích của hình bình hành ấy 
Bài tập 26: Tam giác ABC có AB = 16cm, AC = 14cm, và μ 0 B = 60
a. Tính BC
b. Tính SABC
Bài tập 27: Cho hình bình hành ABCD có μ 0 A= 45 , AB = = BD 18cm
a. Tính AB
b. Tính SABCD 
Bài tập 28: Một cột đèn có bóng trên mặt dài 7,5m, các tia sáng mặt trời tạo với mặt đất một gócxấp xỉ bằng 42. Tính chiều cao của cột đèn.
Bài tập 30: Cho tam giác ABC vuông ở A, đường cao AH. Tính sinB, sinC ứng với mỗi trường hợp sau:
a. AB = = 10cm; 6 BH cm
b. BH = = 5cm; AH 12cm
Bài tập 33: Cho tam giác vuông ABC vuông ở A, AB = = 6cm, 8 AC cm . Tínha. Tính μ μ BC, , B C 
b. Đường phân giác của góc A cắt BC ở D. Tính BD,DC
c. Từ D kẻ DE ^ AB, DF ^ AC. Tứ giác AEDF là hình gì? Tính chu vi và diện tích của tứ giác AEDF.
Bài tập 34: Góc ở đỉnh của một tam giác bằng 78o, cạnh đáy dài 28,5cm. Tính độ dài cạnh bên và diện tích của tam giác
Bài tập 35: Cạnh bên của một tam giác cân dài 17, 2cm , góc ở đáy của tam giác là 46o
. Tính cạnh đáy của tam giác và diện tích tam giác ABC
Bài tập 36: Cho hình thang ABCD, đáy lớn AB = 20cm , cạnh bên AD = 8cm và tạo với đáy lớn AB một góc 65o
a. Tính độ dài đường cao AH, đáy nhỏ CD
b. Tính góc ·ABD và đường chéo BD
Bài tập 37: Cho hình thang ABCD có μ μ 0 A D = = 90 , AD = 30cm , CD =18cm và BC = 20cm .
a. Tính các góc ·ABC, B·CD
b. Tính các góc DA·C,·ADB và độ dài các đường chéo AC, BD
Bài tập 38: Cho tam giác ABC. Biết AB =10, AC = = 24, BC 26 .
a. Chứng minh rằng tam giác ABC vuông ở A
b. Tính sin B ,sinC
c. Tính chiều cao AH và các đoạn thẳng mà chiều cao nó chia ra trên BC
Bài tập 40: Một người quan sát đứng cách một tháp 10m, nhìn thấy dưới một góc là 55o và được phân tích như hình dưới. Tính chiều cao của chiếc tháp này
Bài tập 41: Trên một quả đồi có một tháp cao 100m. Từ đỉnh B và chân C của tháp nhìn điểm A ở chân đồi dưới các góc tương ứng bằng 60o và 30o
Hãy tính chiều cao của quả đồi