Luyện thi Quốc gia môn Hình học không gian

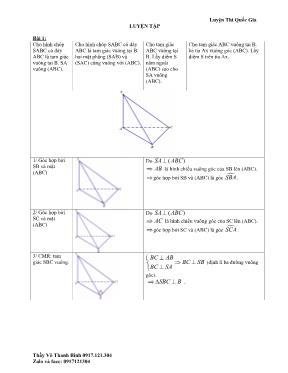
Luyện Thi Quốc Gia 
Thầy Võ Thanh Bình 0917.121.304 
Zalo và face: 0917121304 
LUYỆN TẬP 
Bài 1: 
Cho hình chóp 
SABC có đáy 
ABC là tam giác 
vuông tại B. SA 
vuông (ABC). 
Cho hình chóp SABC có đáy 
ABC là tam giác vuông tại B. 
hai mặt phẳng (SAB) và 
(SAC) cùng vuông với (ABC). 
Cho tam giác 
ABC vuông tại 
B. Lấy điểm S 
nằm ngoài 
(ABC) sao cho 
SA vuông 
(ABC). 
Cho tam giác ABC vuông tại B. 
kẻ tia Ax vuông góc (ABC). Lấy 
điểm S trên tia Ax. 
1/ Góc hợp bởi 
SB và mặt 
(ABC) 
Do ( )SA ABC 
AB là hình chiếu vuông góc của SB lên (ABC). 
 góc hợp bởi SB và (ABC) là góc SBA . 
2/ Góc hợp bởi 
SC và mặt 
(ABC) 
Do ( )SA ABC 
AC là hình chiếu vuông góc của SC lên (ABC). 
 góc hợp bởi SC và (ABC) là góc SCA . 
3/ CMR: tam 
giác SBC vuông. 
BC AB
BC SB
BC SA

 

 (định lí ba đường vuông 
góc). 
 SBC B  . 
Luyện Thi Quốc Gia 
Thầy Võ Thanh Bình 0917.121.304 
Zalo và face: 0917121304 
4/ Góc hợp bởi 
SC và mặt (SAB) 
 
BC AB
BC SAB
BC SA

 

SB là hình chiếu vuông góc của SC lên (SAB). 
 góc hợp bởi SC và (SAB) là góc CSB . 
5/ Góc hợp bởi 
SB và mặt (SAC) 
Gọi E là hình chiếu vuông góc của B lên AC 
( )
BE AC
BE SAC
BE SA

  

SE là hình chiếu vuông góc của SB lên (SAC). 
 góc hợp bởi SB và (SAC) là góc BSE . 
6/ Góc hợp bởi 
(SBC) và mặt 
(ABC) 
   SBC ABC BC
AB BC
SB BC
 


 
 Góc hợp bởi (SBC) và (SAC) là góc tạo bởi hai 
đường thẳng SB và AB hay SBA 
7/ Tính thể tích 
khối SABC. 
1 1
. . .
3 6
SABC ABCV SA S SA AB AC  
8/ Xác định tâm 
và bán kính mặt 
cầu đi qua 4 
điểm S,A,B,C. 
Cách 1: 
Gọi I là trung điểm của SC. 
 (1)SAC A IA IS IC     
(dựa vào câu 3) 
 (2)SBC B IB IS IC     
Từ (1) và (2) suy ra 
 IA IS IC IB   
I là tâm mặt cầu đi qua 4 điểm S,A,B,C. Với bán 
kính 
1
2
R SC . 
Cách 2: (thực hiện 4 bước tổng quát) 
Luyện Thi Quốc Gia 
Thầy Võ Thanh Bình 0917.121.304 
Zalo và face: 0917121304 
9/ Gọi M là trung 
điểm của SB, N 
là điểm trên SC 
sao cho 
NS=2NC. 
Tính thể tích 
khối AMNCB. 
Ta có: 
1 2 1
. .
2 3 3
SAMN
SABC
V SM SN
V SB SC
   
1
3
2
3
SAMN SABC
AMNCB SABC
V V
V V

 
9/ Gọi G là trọng 
tâm tam giác 
SBC. Mp (P) qua 
AG và // BC, cắt 
SB, SC tại M, N. 
Tính thể tích 
khối AMNCB. 
Gọi K là trung điểm BC. G là trọng tâm của tam giác 
SBC 
Trong tam giác SBC qua G kẻ // BC, cắt SB tại M, SC 
tại N. 
/ /
2
3
MN BC
SM SN SG
SB SC SI
   
Ta có: 
4
.
9
SAMN
SABC
V SM SN
V SB SC
  
4
9
5
9
SAMN SABC
AMNCB SABC
V V
V V

 
10/ Gọi H, K lần 
lượt là hình chiếu 
vuông góc của A 
lên SB và SC. 
Tính tỉ lệ thể tích 
của chóp SABC 
được chia bởi 
(AHK). 
2
2 2 2
:
.
SAB A
SH SH SB SA
SB SB SA AB
 
 

2
2 2 2
:
.
SAC A
SK SK SC SA
SC SC SA AC
 
 

Ta có: 
.SAHK
SABC
V SH SK
V SB SC


  
SAHK SABC
AHKCB SABC
SAHK
AHKCB
V V
V V
V
V


 


 


 
 

Luyện Thi Quốc Gia 
Thầy Võ Thanh Bình 0917.121.304 
Zalo và face: 0917121304 
11/ Tính 
  ;d A SBC 
Cách 1: 
Gọi H là hình chiếu của A lên SB 
( 3) : ( )
( )
AH SB
C BC SAB AH AH BC
AH SBC


   
 
  ;d A SBC AH  
Tính AH bằng các công thức sau: 
 
2 2
2 2 2 2 2
1 1 1 .
.
. .
sinSBA .sinSBA
SA AB
AH
AH SA AB SA AB
AB AC
AB AC AH BC AH
BC
AH
AH AB
AB
    

   
   
Cách 2: 
 
 
1
;( ) .
3
3. . .
;( )
.
SABC SBC
SABC
SBC
V d A SBC S
V SA AB AC
d A SBC
S SB BC



  
12/ Tính 
  ;d C SAB 
(C3): ( )BC SAB 
 ;( )d C SAB BC  
13/ Tính 
  B;d SAC 
Gọi E là hình chiếu vuông góc của B lên AC 
( )
BE AC
BE SAC
BE SA

  

  B;d SAC BE 
(tính BE như các công thức C11) 
14/ Tính 
 SA;BCd 
 ;
AB SA
d SA BC AB
AB BC

 

Luyện Thi Quốc Gia 
Thầy Võ Thanh Bình 0917.121.304 
Zalo và face: 0917121304 
14/ Tính 
 SB;ACd 
Gọi P sao cho PACB là hình bình hành. 
     
/ / , (SBP)
d ;SB d ;(SBP) d ;(SBP)
AC BP BP
AC AC A

  
Gọi K là hình chiếu của A lên BP. H là hình chiếu của 
A lên SK. 
 (1)AH SK 
( ) AH
 (2)
BP AK
BP SAK
BP SA
AH BP

  

 
Từ (1), (2) ( )AH SPB 
 d ;(SBP)A AH  
15/ Tính 
 ;d SC AB 
Gọi P sao cho ABCP là hình bình hành. 
Vì  090ABC ABCP  là hình chữ nhật. 
     
/ / , ( )
; ;( ) ;( )
AB CP CP SCP
d AB SC d AB SCP d A SCP

  
Gọi H là hình chiếu của A lên SP. 
 (1)AH SP 
( ) AH
 (2)
CP AP
CP SAP
CP SA
AH CP

  

 
Từ (1), (2) ( )AH SCP 
 d ;(SCP)A AH  
16/ Tính 
  ;d Q SBC . 
Q thuộc AB sao 
cho AQ nQB 
Ta có: 
 
 
QA (SBC) B
d ;(SBC)
d ;(SBC)
Q QB
A QA
 
 
   d ;(SBC) d ;(SBC) 
QB
Q A
QA
  
Bài toán quay về C11. 
17/ Tính 
  ;d G SBC . 
G là trọng tâm 
của tam giác 
SAB. 
Gọi M là trung điểm của AB. G là trọng tâm của tam 
giác SAB. 
 
 
(SBC)
d ;(SBC) 2
d ;(SBC) 3
GM S
G GS
M MS
 
  
   
2
d ;(SBC) d ;(SBC) (1)
3
G M  
Luyện Thi Quốc Gia 
Thầy Võ Thanh Bình 0917.121.304 
Zalo và face: 0917121304 
 
 
(SBC)
d ;(SBC)
2
d ;(SBC)
AM B
A AB
M MB
 
  
   
1
d ;(SBC) .d A;(SBC) (2)
2
M  
Từ (1), (2) suy ra 
   
1
d ;(SBC) d A;(SBC)
3
G  
Bài toán quay về C11. 
Áp dụng thực tế 
AB a , 2BC a , 3AB a 
AB BC a  , 3SB a 
AB a , 2BC a , góc hợp bởi SB và (ABC) là 060 . 
AB a , 5AC a , góc hợp bởi SC và (SAB) là 030 . 
AB a , 5AC a ,    1;
2
d A SBC a 
Bài 2: 
Cho hình chóp SABCD có đáy ABCD là hình vuông. ( ).SA ABCD O AC BD  
Cột thứ 3 chỉ gợi ý. Các em phải nẳm rõ bài 1 để trình bày và lý luận. 
1/ Góc hợp bởi SB và 
mặt (ABCD) 
   ;SB ABCD SBA 
2/ Góc hợp bởi SC và 
mặt (ABCD) 
   ;SC ABCD SCA 
3/ Góc hợp bởi SD và 
mặt (ABCD) 
   ;SD ABCD SDA 
4/ Góc hợp bởi SC và 
mặt (SAB) 
   ;SC SAB CSB 
5/ Góc hợp bởi SC và 
mặt (SAD) 
   ;SC SAD CSD 
6/ Góc hợp bởi (SBC) 
và mặt (ABCD) 
     ;SBC ABCD SBA 
Luyện Thi Quốc Gia 
Thầy Võ Thanh Bình 0917.121.304 
Zalo và face: 0917121304 
7/ Góc hợp bởi (SCD) 
và mặt (ABCD) 
     ;SCD ABCD SDA 
8/ Góc hợp bởi (SBD) 
và mặt (ABCD) 
     ;SBD ABCD SOA 
9/ Góc hợp bởi (SBC) 
và mặt (SAB) 
Gọi H là hình chiếu vuông góc của A lên 
SB. 
Cách 1: 
( ) ( )SAB SBC SB
AH SB
BC SB
 


 
      ; ;SBC SAB AH BC 
Cách 2: 
( )
( )
AH SBC
AD SAB



      ; ;ADSBC SAB AH 
10/ Góc hợp bởi 
(SCD) và mặt (SAD) 
Tương tự C9 
    
 
 
;
;
;AB
SBC SAB
AH CD
AH


11/ Góc hợp bởi 
(SBC) và mặt (SCD) 
Cách 1: 
Gọi H là hình chiếu vuông góc của B lên SC 
( khi đó H cũng là hình chiếu vuông góc của 
D lên SC). 
      ; ;DHSBC SCD BH 
Cách 2: 
Gọi M, N lần lượt là hình chiếu vuông góc 
của A lên SB, SD. 
      ; ;SBC SCD AM AN 
12/ Tính thể tích các 
khối:.. 
21 1. .
3 3
SABCD ABCDV SA S SA AB  
1
2
SABC SABD SACD SBCD SABCDV V V V V    
Luyện Thi Quốc Gia 
Thầy Võ Thanh Bình 0917.121.304 
Zalo và face: 0917121304 
13/ Xác định tâm và 
bán kính mặt cầu 
ngoại tiếp chóp 
SABCD 
Cách 1: 
Gọi I là trung điểm của SC. 
 (1)SAC A IA IS IC     
 (2)SBC B IB IS IC     
 (3)SCD D ID IS IC     
Từ (1), (2) và (3) suy ra 
 IA IB IC ID IS    
I là tâm mặt cầu ngoại tiếp chóp 
SABCD với bán kính 
1
2
R SC 
Cách 2: (thực hiện 4 bước tổng quát) 
14/ Tính 
  ;d A SBC 
Gọi H là hình chiếu vuông góc của A lên 
SB. 
  ;d A SBC AH 
15/ Tính 
  ;d A SCD 
Gọi H là hình chiếu vuông góc của A lên 
SD. 
  ;d A SBC AH 
16/ Tính 
  ;d A SBD 
Gọi H là hình chiếu vuông góc của A lên 
SO. 
  ;d A SBD AH 
17/ Tính 
  ;d B SCD 
Gọi H là hình chiếu vuông góc của A lên 
SD. 
Do / /( )AB SCD 
   B;( ) A;( )d SCD d SCD AH   
Luyện Thi Quốc Gia 
Thầy Võ Thanh Bình 0917.121.304 
Zalo và face: 0917121304 
18/ Tính 
  ;d M SCD . Với 
M thuộc AB. 
Gọi H là hình chiếu vuông góc của A lên 
SD. 
Do / /( )AB SCD , M AB 
   M;( ) A;( )d SCD d SCD AH   
19/ Tính 
  O;d SCD . 
Gọi H là hình chiếu vuông góc của A lên 
SD. 
Do ( ) CAO SCD  
 
 
;( )
2
O;( )
d A SCD AC
d SCD OC
   
 
1
;( )
2
d O SCD AH  
20/ Tính 
  ;d P SCD . Với 
P là trung điểm BO. 
Gọi H là hình chiếu vuông góc của A lên 
SD. 
Do ( )PB SCD O  
 
 
P;( ) 1
B;( ) 2
d SCD PO
d SCD BO
   
   
1
P;( ) B;( )
2
d SCD d SCD  
Do / /( )AB SCD 
   ;( ) B;( )d A SCD d SCD  
Vậy:    
1
P;( ) ;( )
2
d SCD d A SCD 
21/ Tính 
  ;d G SCD . Với 
G là trọng tâm của 
tam giác SAB 
Gọi H là hình chiếu vuông góc của A lên 
SD. M là trung điểm AB. 
   
   
 
2
;( ) M;( )
3
M;( ) ;( )
2
;( )
3
d G SCD d SCD
d SCD d A SCD
d G SCD AH


 
22/ Tính 
 ;d SB AD . 
Gọi H là hình chiếu vuông góc của A lên SB 
 ;d SB AD AH 
Luyện Thi Quốc Gia 
Thầy Võ Thanh Bình 0917.121.304 
Zalo và face: 0917121304 
23/ Tính 
 ;SCd AB . 
Cách 1: 
Gọi H là hình chiếu vuông góc của B lên SC 
 ;SCd AB BH 
Cách 2: 
Gọi K là hình chiếu vuông góc của A lên SD 
/ /(SCD)AB 
 
  
  
;SC
; SCD
; SCD
d AB
d AB
d A AK


 
24/ Tính 
 ;SCd BD . 
Gọi H là hình chiếu vuông góc của O lên SC 
 ;SCd BD OH 
25/ Tính 
 SC;ADd . 
Gọi H là hình chiếu vuông góc của A lên SB 
   
 
/ /( )
d ; ;(S )
;( )
AD SCB
AD SC d AD CB
d A SCB AH
 
 
26/ Tính 
 ;d SB CD . 
 ;d SB CD AD 
27/ Tính 
 ;d BM CD . Với M 
là trung điểm SC. 
Gọi K là trung điểm AB, H là hình chiếu 
vuông góc của O lên AK. 
   
 
 
/ / AB ( )
/ /( )
d ; ;( )
;( )
1 1
O;( )
2 2
CD MAB
CD MAB
CD BM d CD MAB
d C MAB
d MAB OH


 

 
Luyện Thi Quốc Gia 
Thầy Võ Thanh Bình 0917.121.304 
Zalo và face: 0917121304 
28/ Gọi H, I, K lần 
lượt là hình chiếu 
vuông góc của A lên 
SB, SC, SK. 
CMR: A,H,I,K đồng 
phẳng. 
Tính thể tích khối 
SAHIK. 
Gợi ý: ( )
SC AH
SC AHK
SC AK

 

Mà AI SC 
( )AI AHK   
Ta có: 
2 2
2 2 2 2
.
.
2 2
SAHI
SABC
SAHI SABC
SAHI SABC
SAHIK SABCD
V SH SI
V SB SC
SA SA
SA AB SA AC
V V
V V
V V





 
 
 
 
 
29/ Gọi G là trong tâm 
tam giác SBD. (P) qua 
AG song song BD cắt 
SB, SC, SD tại M, N, 
Q. 
Tính thể tích khối 
SAMNQ. 
1
.
3
1
3
1
2 .2
3
1
3
SAMN
SABC
SAMN SABC
SAMN SABC
SAMNQ SABCD
V SM SN
V SB SC
V V
V V
V V
 
 
 
 
Áp dụng thực tế 
AB a , 2SB a 
2AB a , góc hợp bởi của SC và mặt (ABCD) là 045 
AB a , góc hợp bởi của (SBD) và mặt (ABCD) là 030 
SB a , góc hợp bởi của SC và mặt (SAB) là 060 
Bài 3: 
Cho hình chóp SABCD có đáy ABCD là hình chữ nhật. ( ).SA ABCD O AC BD  
Cột thứ 3 chỉ gợi ý. Các em phải nẳm rõ bài 1 để trình bày và lý luận. 
Luyện Thi Quốc Gia 
Thầy Võ Thanh Bình 0917.121.304 
Zalo và face: 0917121304 
1/ Góc hợp bởi SB và 
mặt (ABCD) 
   ;SB ABCD SBA 
2/ Góc hợp bởi SC và 
mặt (ABCD) 
   ;SC ABCD SCA 
3/ Góc hợp bởi SD và 
mặt (ABCD) 
   ;SD ABCD SDA 
4/ Góc hợp bởi SC và 
mặt (SAB) 
   ;SC SAB CSB 
5/ Góc hợp bởi SC và 
mặt (SAD) 
   ;SC SAD CSD 
6/ Góc hợp bởi (SBC) 
và mặt (ABCD) 
     ;SBC ABCD SBA 
7/ Góc hợp bởi (SCD) 
và mặt (ABCD) 
     ;SCD ABCD SDA 
8/ Góc hợp bởi (SBD) 
và mặt (ABCD) 
     ;SBD ABCD SOA 
9/ Góc hợp bởi (SBC) 
và mặt (SAB) 
Gọi H là hình chiếu vuông góc của A lên 
SB. 
Cách 1: 
( ) ( )SAB SBC SB
AH SB
BC SB
 


 
      ; ;SBC SAB AH BC 
Cách 2: 
( )
( )
AH SBC
AD SAB



      ; ;ADSBC SAB AH 
10/ Góc hợp bởi 
(SCD) và mặt (SAD) 
Tương tự C9 
    
 
 
;
;
;AB
SBC SAB
AH CD
AH


Luyện Thi Quốc Gia 
Thầy Võ Thanh Bình 0917.121.304 
Zalo và face: 0917121304 
11/ Góc hợp bởi 
(SBC) và mặt (SCD) 
Cách 1: 
Gọi H là hình chiếu vuông góc của B lên SC 
( khi đó H cũng là hình chiếu vuông góc của 
D lên SC). 
      ; ;DHSBC SCD BH 
Cách 2: 
Gọi M, N lần lượt là hình chiếu vuông góc 
của A lên SB, SD. 
      ; ;SBC SCD AM AN 
12/ Tính thể tích các 
khối:.. 
21 1. .
3 3
SABCD ABCDV SA S SA AB  
1
2
SABC SABD SACD SBCD SABCDV V V V V    
13/ Xác định tâm và 
bán kính mặt cầu 
ngoại tiếp chóp 
SABCD 
Cách 1: 
Gọi I là trung điểm của SC. 
 (1)SAC A IA IS IC     
 (2)SBC B IB IS IC     
 (3)SCD D ID IS IC     
Từ (1), (2) và (3) suy ra 
 IA IB IC ID IS    
I là tâm mặt cầu ngoại tiếp chóp 
SABCD với bán kính 
1
2
R SC 
Cách 2: (thực hiện 4 bước tổng quát) 
14/ Tính 
  ;d A SBC 
Gọi H là hình chiếu vuông góc của A lên 
SB. 
  ;d A SBC AH 
15/ Tính 
  ;d A SCD 
Gọi H là hình chiếu vuông góc của A lên 
SD. 
  ;d A SBC AH 
Luyện Thi Quốc Gia 
Thầy Võ Thanh Bình 0917.121.304 
Zalo và face: 0917121304 
16/ Tính 
  ;d A SBD 
Gọi H là hình chiếu vuông góc của A lên 
SO. 
  ;d A SBD AH 
17/ Tính 
  ;d B SCD 
Gọi H là hình chiếu vuông góc của A lên 
SD. 
Do / /( )AB SCD 
   B;( ) A;( )d SCD d SCD AH   
18/ Tính 
  ;d M SCD . Với 
M thuộc AB. 
Gọi H là hình chiếu vuông góc của A lên 
SD. 
Do / /( )AB SCD , M AB 
   M;( ) A;( )d SCD d SCD AH   
19/ Tính 
  O;d SCD . 
Gọi H là hình chiếu vuông góc của A lên 
SD. 
Do ( ) CAO SCD  
 
 
;( )
2
O;( )
d A SCD AC
d SCD OC
   
 
1
;( )
2
d O SCD AH  
20/ Tính 
  ;d P SCD . Với 
P là trung điểm BO. 
Gọi H là hình chiếu vuông góc của A lên 
SD. 
Do ( )PB SCD O  
 
 
P;( ) 1
B;( ) 2
d SCD PO
d SCD BO
   
   
1
P;( ) B;( )
2
d SCD d SCD  
Do / /( )AB SCD 
   ;( ) B;( )d A SCD d SCD  
Vậy:    
1
P;( ) ;( )
2
d SCD d A SCD 
Luyện Thi Quốc Gia 
Thầy Võ Thanh Bình 0917.121.304 
Zalo và face: 0917121304 
21/ Tính 
  ;d G SCD . Với 
G là trọng tâm của 
tam giác SAB 
Gọi H là hình chiếu vuông góc của A lên 
SD. M là trung điểm AB. 
   
   
 
2
;( ) M;( )
3
M;( ) ;( )
2
;( )
3
d G SCD d SCD
d SCD d A SCD
d G SCD AH


 
22/ Tính 
 ;d SB AD . 
Gọi H là hình chiếu vuông góc của A lên SB 
 ;d SB AD AH 
23/ Tính 
 ;SCd AB . 
Cách 1: 
Gọi H là hình chiếu vuông góc của B lên SC 
 ;SCd AB BH 
Cách 2: 
Gọi K là hình chiếu vuông góc của A lên SD 
/ /(SCD)AB 
 
  
  
;SC
; SCD
; SCD
d AB
d AB
d A AK


 
24/ Tính 
 ;SCd BD . 
Gọi H là hình chiếu vuông góc của O lên SC 
 ;SCd BD OH 
25/ Tính 
 SC;ADd . 
Gọi H là hình chiếu vuông góc của A lên SB 
   
 
/ /( )
d ; ;(S )
;( )
AD SCB
AD SC d AD CB
d A SCB AH
 
 
Luyện Thi Quốc Gia 
Thầy Võ Thanh Bình 0917.121.304 
Zalo và face: 0917121304 
26/ Tính 
 ;d SB CD . 
 ;d SB CD AD 
27/ Tính 
 ;d BM CD . Với M 
là trung điểm SC. 
Gọi K là trung điểm AB, H là hình chiếu 
vuông góc của O lên AK. 
   
 
 
/ / AB ( )
/ /( )
d ; ;( )
;( )
1 1
O;( )
2 2
CD MAB
CD MAB
CD BM d CD MAB
d C MAB
d MAB OH


 

 
28/ Gọi H, I, K lần 
lượt là hình chiếu 
vuông góc của A lên 
SB, SC, SK. 
CMR: A,H,I,K đồng 
phẳng. 
Tính thể tích khối 
SAHIK. 
Gợi ý: ( )
SC AH
SC AHK
SC AK

 

Mà AI SC 
( )AI AHK   
Ta có: 
2 2
2 2 2 2
.
.
2 2
SAHI
SABC
SAHI SABC
SAHI SABC
SAHIK SABCD
V SH SI
V SB SC
SA SA
SA AB SA AC
V V
V V
V V





 
 
 
 
 
29/ Gọi G là trong tâm 
tam giác SBD. (P) qua 
AG song song BD cắt 
SB, SC, SD tại M, N, 
Q. 
Tính thể tích khối 
SAMNQ. 
1
.
3
1
3
1
2 .2
3
1
3
SAMN
SABC
SAMN SABC
SAMN SABC
SAMNQ SABCD
V SM SN
V SB SC
V V
V V
V V
 
 
 
 
Áp dụng thực tế 
AB a , 2SB a 
2AB a , 2SB a , góc hợp bởi của SC và mặt (ABCD) là 045 
Luyện Thi Quốc Gia 
Thầy Võ Thanh Bình 0917.121.304 
Zalo và face: 0917121304 
AB a , 2SB a , góc hợp bởi của (SBD) và mặt (ABCD) là 030 
SB a , 2SB a , góc hợp bởi của SC và mặt (SAB) là 060 
Bài 4: 
cho hình chóp tam giác đều SABC. M là trung điểm BC, O là tâm của tam giác ABC. 
1/ góc hợp bởi cạnh bên và 
mặt đáy 
    ;SA ABC SAO 
2/ góc hợp bởi mặt bên và 
mặt đáy 
      ;SBC ABC SMA 
3/ thể tích khối chớp SABC 
21 3. .
3 12
SABC ABCV SO S SO AB  
4/ Tính 
  
  
  
;
;
;
d A SBC
d B SAC
d C SAB


cách 1: 
  
3
; SABC
SBC
V
d A SBC
S
 
cách 2: 
gọi H là hình chiếu vuông góc của O 
lên SM. 
     ; 3 ; 3d A SBC d O SBC OH  
5/ Tính 
 
 
 
;
;
;
d SA BC
d SB AC
d SC AB


gọi H là hình chiếu vuông góc của M 
lên SA. 
   ; ;d SA BC d M SA MH  
Luyện Thi Quốc Gia 
Thầy Võ Thanh Bình 0917.121.304 
Zalo và face: 0917121304 
6/ xác định tâm và bán kính 
mặt cầu ngoại tiếp hình chóp 
SABC 
SO là trục của tam giác ABC. 
gọi N là trung điểm SA. dựng mp 
trung trực của SA cắt SO tại I. 
IA IB IC IS    
 I là tâm mặt cầu ngoại tiếp hình 
chóp SABC, bán kính R=IS. 
để tính IS ta dùng: 
cách 1: 
IS NS
NSI OSA
SA SO
     
2
2
SA
R IS
SO
   
cách 2: 
cos
SN
R IS
NSI
  
7/ Tính thể tích khối nón 
ngoại tiếp chóp SABC. 
chóp SABC nội tiếp trong hình nón 
có bán kính R=OA; chiều cao h=SO 
và đường sinh l=SA 
21 . .
3
nonV SO OA 
8/ Tính thể tích khối trụ 
ngoại tiếp chóp SABC. 
chóp SABC nội tiếp trong hình trụ có 
bán kính R=OA; chiều cao h=SO 
2. .truV SO OA 
9/ gọi E là trung điểm AB. 
Tính  ;d EC SB 
gọi P sao cho BECP là hinh bình 
hành. 
CE vuông AB nên BECP là hình chữ 
nhật. 
kể gọi K thuộc BP sao cho OK song 
song EB. 
gọi H là hình chiếu của O lên SK. 
    
     
; ;
; ;
d EC SB d EC SBP
d EC SBP d O SBP
OH

 

Luyện Thi Quốc Gia 
Thầy Võ Thanh Bình 0917.121.304 
Zalo và face: 0917121304 
10/ gọi E là trung điểm AB. 
Tính  ;d EC BC 
gọi F là trung điểm AC. 
K giao điểm AM với EF. 
H là hình chiếu của O lên SK. 
    
  
  
; ;
C;
3 ; 3
d EC BC d BC SEF
d SEF
d O SEF OH


 
Áp dụng thực tế 
Cạnh đáy bằng a , cạnh bên bằng 3a 
Cạnh đáy bằng a , cạnh bên hợp mặt đáy góc một góc 060 
Cạnh đáy bằng 2a , mặt bên hợp mặt đáy góc một góc 030 
cạnh bên bằng 3a , mặt bên hợp mặt đáy góc một góc 030 
Cạnh đáy bằng a , diện tích tam giác SAC bằng 24a 
Cạnh đáy bằng 2a , khoảng cách từ A đến (SBC) là 3a 
Bài 5: 
cho hình chóp tứ giác đều SABCD. M là trung điểm CD, O là tâm của ABCD. 
1/ góc hợp bởi cạnh bên 
và mặt đáy 
    ;SA ABCD SAO 
2/ góc hợp bởi mặt bên 
và mặt đáy 
      ;SCD ABCD SMO 
3/ thể tích khối chớp 
SABC 
 21 1. .
3 3
SABCD ABCDV SO S SO AB  
Luyện Thi Quốc Gia 
Thầy Võ Thanh Bình 0917.121.304 
Zalo và face: 0917121304 
4/ Tính 
  
  
  
  
;
;
;
B;
...
d A SCD
d A SBC
d B SCD
d SAD



gọi H là hình chiếu vuông góc của O 
lên SM. 
     ; 2 O; 2d A SCD d SCD OH  
5/ Tính 
 
 
 
 
;
;
;CD
;AD
......
d SA BC
d SA CD
d SB
d SB




gọi H là hình chiếu vuông góc của O 
lên SM. 
 
  
  
  
;
;
;
2 ;
2
d SB CD
d SB SCD
d B SCD
d O SCD
OH




6/ xác định tâm và bán 
kính mặt cầu ngoại tiếp 
hình chóp SABCD 
SO là trục của ABCD. 
gọi N là trung điểm SA. dựng mp 
trung trực của SA cắt SO tại I. 
IA IB IC ID IS     
 I là tâm mặt cầu ngoại tiếp hình 
chóp SABCD, bán kính R=IS. 
để tính IS ta dùng: 
cách 1: 
IS NS
NSI OSA
SA SO
     
2
2
SA
R IS
SO
   
cách 2: 
cos
SN
R IS
NSI
  
Áp dụng thực tế 
Cạnh đáy bằn