Kiểm tra học kỳ 1 lớp 12 THPT - Năm học 2015 – 2016 môn Toán

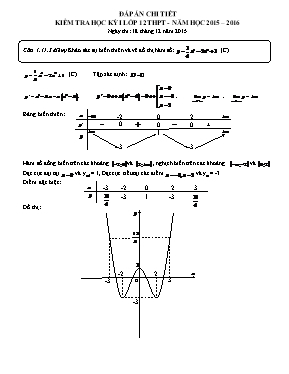
ĐÁP ÁN CHI TIẾT
KIỂM TRA HỌC KỲ I LỚP 12 THPT - NĂM HỌC 2015 – 2016
Ngày thi: 18 tháng 12 năm 2015
Câu 1. (1,5 điểm) Khảo sát sự biến thiên và vẽ đồ thị hàm số: (C)
 (C)	 Tập xác định: 
0
0
0
-2
0
1
-3
-3
2
; ; ; 
Bảng biến thiên: 
Hàm số đồng biến trên các khoảng và , nghịch biến trên cac khoảng và 
Đạt cực đại tại và ycđ = 1, Đạt cực tiểu tại các điểm và yct = -3
-3 
0 
-3 
-2 
2 
3 
Điểm đặc biệt: 
-3 
1 
-3 
3 
2 
-2 
-3 
o 
Đồ thị: 
Câu 2 ( 1 điểm) Tìm giá trị lớn nhất của hàm số: trên đoạn 
Hàm số xác định và liên tục trên đoạn , ta có: 
 Ta có: ; 
Vậy: 
Câu 3 ( 1,5 điểm) 	1) Tính . Tìm tiệm cận ngang của đồ thị hàm số: 
 2) Tính đạo hàm của hàm số: 
1) , Tìm tiệm cận ngang của đồ thị hàm số: là trục hoành: 
2) ; 
Câu 4 ( 1,5 điểm) 1) Giải phương trình: 
 2) Tìm các số thực thỏa: 
Vậy nghiệm của phương trình là: 
 2) (1) ; điều kiện: (*)
Bất phương trình (1) tương đương với: 
So với điều kiện (*), ta có: 
Vậy: là các số thực cần tìm.
Câu 5 ( 1 điểm) Cho hình vuông ABCD có , với là số thực dương. Gọi M,N tương ứng là trung điểm của hai cạnh AB và CD. Gọi (T) là hình trụ tròn xoay sinh ra bởi hình vuông ABCD quay quanh đường thẳng MN.
Tính theo diện tích xung quanh của hình trụ (T). 
Tính theo thể tích khối trụ tròn xoay giới hạn bởi hình trụ (T) 
A
B
D
N
M
C
 Ta có: Đường sinh của hình trụ: 
 Đường cao của hình trụ: 
 Bán kính đáy: 
Diện tích xung quanh của hình trụ (T): (đvdt)
Thể tích của khối trụ (T): (đvtt)
Câu 6 ( 1,5 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng (ABCD), góc giữa đường thẳng SB và mặt phẳng (ABCD) bằng , biết , , với là số thực dương.
Tính theo thể tích khối chóp S.ABCD
Tính theo khoảng cách từ điểm B đến mặt phẳng (SCD)
S
A
B
C
D
H
)
600
Thể tích khối chóp S.ABCD
Diện tích hình chữ nhật ABCD: 
AB là hình chiếu vuông góc của SB trên mặt phẳng (ABCD)
 góc giữa SB và (ABCD) là 
Tam giác SAB vuông tại A, ta có: 
Vậy: (đvtt)
2) Khoảng cách từ điểm B đến mặt phẳng (SCD) 
Gọi H là hình chiếu vuông góc của A trên SD 
Do đó: 
Tam giác SAD vuông tại A, ta có: 
 Vậy: (đvđd)
Câu 7 ( 1 điểm) Tìm tập xác định của hàm số: 
 Hàm số xác định khi: 
hoặc
hoặc
hoặc
hoặc
hoặc
hoặc
hoặc
hoặc
Vậy: tập xác định của hàm số: 
Câu 8 ( 1 điểm) Cho hình hộp chữ nhật có ; với là ba số thực dương thỏa 
Chứng minh: 
B1
A1
B1
C1
D
C
B
A
Tìm giá trị nhỏ nhất của 
Chứng minh: 
Tam giác ABC vuông tại B:
Tam giác ACC1 vuông tại C:
2) Tìm giá trị nhỏ nhất của 
Ta có: 
Do đó: khi: 
Hướng dẫn giải phương trình bậc 4: