Kiểm tra chương III – Hình học 9

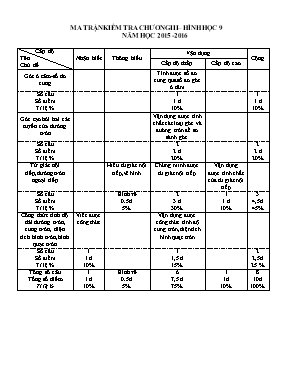
MA TRẬN KIỂM TRA CHƯƠNG III– HÌNH HỌC 9
NĂM HỌC 2015 -2016
 Cấp độ
Tên 
Chủ đề 
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
Góc ở tâm-số đo cung
Tính được số đo cung.qua số đo góc ở tâm
Số câu
Số điểm
Tỉ lệ %
1
1 đ
10%
1
1 đ
10%
Góc tạo bởi hai cát tuyến của đường tròn
Vận dụng được tính chất các loại góc và đường tròn để so sánh góc
Số câu
Số điểm
Tỉ lệ %
2
2 đ
20%
2
2 đ
20%
Tứ giác nội tiếp,đường tròn ngoại tiếp
Hiểu tứ giác nội tiếp,vẽ hình
Chứng minh được tứ giác nội tiếp. 
Vận dụng được tính chất của tứ giác nội tiếp
Số câu
Số điểm
Tỉ lệ %
Hình vẽ
0.5đ
5%
2
3 đ
30%
1
1 đ
10%
3
4,5đ
45%
Công thức tính độ dài đường tròn, cung tròn, diện tích hình tròn,hình quạt tròn
Viết được công thức
Vận dụng được công thức tính độ cung tròn,diện tích hình quạt tròn
Số câu
Số điểm
Tỉ lệ %
1
1 đ
10%
1
1,5 đ
15%
2
2,5đ
25 %
Tổng số câu
Tổng số điểm
Tỉ lệ %
1
1 đ
10%
Hình vẽ
0.5đ
5%
6
7,5 đ
75%
1
1đ
10%
8
10đ
100%
KIỂM TRA CHƯƠNG III HÌNH HỌC 9 NĂM HỌC 2015-2016
Thời gian làm bài:45 phút
ĐỀ BÀI:
Câu 1: (4 điểm)
1)Viết công thức tính diện tích hình tròn và diện tích hình quạt tròn cung tròn n0 
2)Cho hình vẽ
Biết Cx là tiếp tuyến tại C của đường tròn (O), = 600, AB là đường kính của đường tròn, AB = 6cm. Tính:
 a)Số đo góc BOC 	
 b)Số đo góc BCx	
 c)Số đo góc CDB	
 d)Độ dài cung BmC và diện tích hình quạt tròn OBmC 	
Bài 2: (6điểm) Cho đường tròn (O) đường kính BC, A là một điểm thuộc (O) sao cho AB < AC, D là điểm giữa O và C. Đường thẳng vuông góc với BC tại D cắt AC tại E và cắt đường thẳng AB tại F.	
Chứng minh các tứ giác ABDE và ADCF nội tiếp.
Chứng minh: 
Tiếp tuyến tại A của (O) cắt DE tại M. Chứng minh tam giác AME cân tại M.
Gọi I là tâm đường tròn ngoại tiếp tứ giác ADCF. Chứng minh OI vuông góc với AC
HẾT
ĐÁP ÁN VÀ BIỂU ĐIỂM
Bài
Nội dung
Điểm
1
1)
2)
Viết đúng mỗi công thức (0,5đ)	
a/ (góc nội tiếp và góc ở tâm cùng chắn )
b/(góc tạo bởi tia tiếp và dây cung và góc nội tiếp cùng chắn )
c/ (Góc nội tiếp và góc ở tâm cùng chắn cung CmB)
d/Vì AB là đường kính của đường (O)
Nên OA = 
là góc ở tâm chắn 
 nên sđ= = 1200
Độ dài l của cung CmB là:
Gọi S là diện tích hình quạt tròn OCmB, ta có:
S = 
1đ
3đ
0,5đ
0,5đ
0,5đ
0,25đ
0,25đ
0,5 đ
0,5 đ
2
HV
Hình vẽ đúng , đủ tới câu a
0,5 đ
a
*Chứng minh tứ giác ABDE nội tiếp đường tròn
( góc nội tiếp chắn nửa đường tròn (O))
(gt)	
Tứ giác ABDE có nên nội tiếp đường tròn 
*Chứng minh tứ giác ADCF nội tiếp đường tròn	
(Kề bù với )
(gt)	
Tứ giác ADCF có 2 đỉnh A và D kề nhau cùng nhìn cạnh CF dưới một góc bằng nhau nên là tứ giác nội tiếp. 	
1,5đ 
0,5đ
0,5đ
0,5đ
1,5đ 0,5đ
0,5đ
0,5đ
b
Chứng minh: 
 ( 2 góc kề bù)
 (ABDE là tứ giác nội tiếp)
Suy ra 
1đ
0,25đ
0,5đ
0,25đ
c
Chứng minh tam giác AME cân tại M.
 (cùng chắn cung AC của đường tròn O)
 (cmt)
Suy ra hay DAME cân tại M.
1đ 0,5đ
0,25đ
0,25đ
d
Tứ giác ADCF nội tiếp (cmt) mà (gt) nên CF là đường kính của đường tròn ngoại tiếp tứ giác ADCF. Vậy tâm I của đường tròn ngoại tiếp tứ giác ADCF là trung điểm của CF
Tam giác BCF có OI là đường trung bình nên OI//AB
Mà AB ^ AC tại A nên OI ^ AC
0,5đ
0,25đ
0,25đ