Kiểm tra chương I - Hỉnh học 8 - Chủ đề: Tứ giác - Trường THCS Hành Minh

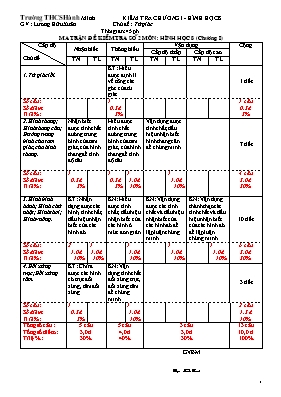
Trường THCS Hành Minh KIỂM TRA CHƯƠNG I - HỈNH HỌC 8
GV : Lương Hữu Xuân Chủ đề: Tứ giác
 Thời gian: 45 ph
MA TRẬN ĐỀ KIỂM TRA SO Á2 MÔN : HÌNH HỌC 8 (Chương I)
 Cấp độ
Chủ đề 
Nhận biết
Thơng hiểu
Vận dụng
Cộng
 Cấp độ thấp
Cấp độ cao
TN
TL
TN
TL
TN
TL
TN
TL
1. Tứ giác lồi.
KT: Hiểu được định lí về tổng các gĩc của tứ giác
1 tiết
Số câu : 
Số điểm: 
Tỉ lệ %:
1
0,5đ
5%
1 câu
0,5 đ
5% 
2. Hình thang; Hình thang cân; Đường trung bình của tam giác, của hình thang.
Nhận biết được tính chất đường trung bình của tam giác, của hình thang để tính độ dài.
Hiểu được tính chất đường trung bình của tam giác, của hình thang để tính độ dài.
Vận dụng được tính chất, dấu hiệu nhận biết hình thang cân để chứng minh
.
7 tiết
Số câu : 
Số điểm: 
Tỉ lệ %:
1
0,5đ
5%
1
0,5đ
5%
1
1,0đ
10%
1
1,0đ
10%
4 câu
3,0 đ
30% 
3. Hình bình hành; Hình chữ nhật; Hình thoi; Hình vuơng.
KT: Nhận dạng được các hình, tính chất, dấu hiệu nhận biết của các hình đĩ
KN: Hiểu được tính chất, dấu hiệu nhận biết của các hình ở mức đơn giản
KN: Vận dụng được các tính chất và dấu hiệu nhận biết của các hình đĩ để lập luận chứng minh.
KN: Vận dụng thành thạo các tính chất và dấu hiệu nhận biết của các hình đĩ để lập luận chứng minh.
10 tiết
Số câu : 
Số điểm: 
Tỉ lệ %:
2
1,0đ
10%
1
1,0đ
10%
1
1,0đ
10%
1
1,0đ
10%
1
1,0đ
10%
6 câu
5,0 đ
50% 
4. Đối xứng trục; Đối xứng tâm.
KT: Chỉ ra được các hình cĩ trục đối xứng, tâm đối xứng.
KN: Vận dụng tính chất đối xứng trục, đối xứng tâm để chứng minh
3 tiết
Số câu : 
Số điểm: 
Tỉ lệ %:
1
0,5đ
5%
1
1,0đ
10%
2 câu
1,5 đ
10% 
Tổng số câu :
Tổng số điểm:
Tỉ lệ %:
5 câu
3,0 đ
30%
5 câu
4,0 đ
40%
3 câu
3,0 đ
30%
13 câu
10,0 đ
100%
 GVBM
 L­¬ng H÷u Xu©
Trường THCS Hành Minh 	KIỂM TRA 1 TIẾT – HÌNH HỌC 8 / HKI
Họ và tên: 	Chủ đề: Tứ giác
Lớp: 	Thời gian: 45 ph
Điểm
Lời phê
Chữ ký của phụ huynh
ĐỀ 1:
I) Trắc nghiệm: (3,0đ). Chọn phương án đúng (Từ câu 1 – câu 4)
Câu 1:Các gĩc của tứ giác cĩ thể là :
 A. 4 gĩc nhọn ;B. 4 gĩc tù ;C. 4 gĩc vuơng ;D. 1 gĩc vuơng, 3 gĩc nhọn
Câu 2: Trong các hình sau, hình nào khơng cĩ trục đối xứng ? 
 A. Hình thang cân ;B. Hình bình hành ;C. Hình chữ nhật ;D. Hình thoi
Câu 3: Cho hình thang ABCD (AB//CD) cĩ AB = 6cm; CD = 16cm. Đường trung bình MN cĩ độ dài bằng:
 A. 22cm	 ;B. 11cm	 ;C. 22,5cm	 ;D. 10cm
Câu 4:Cho tứ giác ABCD. Gọi E,F,K theo thứ tự là trung đđiểm của AD, BC, AC. Kết luận nào sau đây là đúng ?
 A. EF = ;B. EF 
Câu 5: Hãy điền vào chỗ (.) các cụm từ thích hợp để được câu đúng :
 a) Hình vuơng cĩ đường chéo bằng 6cm thì cạnh hình vuơng bằng ..
 b) Tứ giác cĩ 1 cặp cạnh đốithì nĩ là hình bình hành
II) Tự luận: (7,0đ)
Bài 1:(1,0đ). Cho tam giác ABC vuơng tại A, cĩ AB = 7cm ; AC = 24cm. Tính độ dài đường trung bình của tam giác song song với cạnh BC ?
Bài 2:(6,0đ). Cho tam giác ABC vuơng tại A, điểm D là trung điểm của BC. Gọi M là điểm đối xứng với D qua AB, E là giao điểm của DM và AB. Gọi N là điểm đối xứng với D qua AC, F là giao điểm của DN và AC.
 a) Tứ giác AEDF là hình gì ? Vì sao ?
 b) Tứ giác ADBM là hình gì ? Vì sao ?
 c) BN cắt AD tại I. Chứng minh IA = ID
 d) Khi , chứng minh tứ giác ABCN là hình thang cân.
 e) Chứng minh rằng M đối xứng với N qua A.
 f) Tam giác vuơng ABC cĩ điều kiện gì thì tứ giác AEDF là hình vuơng ?
BÀI LÀM
Trường THCS Hành Minh 	ĐÁP ÁN ĐỀ 1 KIỂM TRA HÌNH HỌC 8
GV : Lương Hữu Xuân Chủ đề: Tứ giác
 Thời gian: 45 ph
I) Trắc nghiệm: (3,0đ). Mỗi câu đúng cho 0,5đ
Câu
1
2
3
4
5.a
5.b
Đáp án
C
B
B
C
cm
Vừa s.song vừa bằng nhau
II) Tự luận: (7,0đ)
Bài
Câu
Nội dung đáp án
Điểm
Bài 1: (1,0đ)
-Tính đúng BC = 25cm 
-Tính đúng độ dài đường trung bình 
MN = 12,5cm 
0,5đ
0,5đ
Bài 2: (6,0đ)
a)
Vẽ hình đúng 
Ta cĩ 
 Tứ giác AEDF là hình chữ nhật. 
0,5đ
0,5đ
0.25đ
b)
.∆ABC cĩ BD = DC, DE // AC nên AE = BE.
.Ta lại cĩ DE = EM (D đối xứng với M qua AB). 
Þ ADBM là hình bình hành. 
.Hình bình hành ADBM cĩ hai đường chéo AD ^ BM nên nĩ là hình thoi. 
0,25đ
0,5đ
0,25đ
c)
.Chứng minh tứ giác AMDC là hình bình hành
.Mà I là giao điểm của hai đường chéo nên IA = ID
0,5đ
0,5đ
d)
.Chứng minh AN//BC 
.Chứng minh (cùng bằng 600) 
Suy ra tứ giác ABCN là hình thang cân. 
0,25đ
0,75đ
e)
.Chứng minh M, A, N thẳng hàng (1) 
. AM = AN (2)
Từ (1) và (2) suy ra A là trung điểm của MN, do đĩ M đối xứng với N qua A. 
0,25đ
0,25đ
0,5đ
f)
Hình chữ nhật AEDF là hình vuơng Û AE = AF.
Ta lại cĩ AE = AB; AF = AC 
Nên AE = AF Û AB = AC.
Vậy nếu ∆ABC vuơng cân tại A thì AEDF là hình vuơng. 
0,5đ
0,5đ
 GVBM
 L­¬ng H÷u Xu©n
Trường THCS Hành Minh	KIỂM TRA 1 TIẾT – HÌNH HỌC 8 / HKI
Họ và tên:	Chủ đề: Tứ giác
Lớp:	Thời gian: 45 ph
Điểm
Lời phê
Chữ ký của phụ huynh
ĐỀ 2:
I/ Phần trắc nghiệm (3,0đ). Chọn phương án đúng (Từ câu 1 – câu 4)
Câu 1: Tứ giác ABCD cĩ thì :
 A. ;B. ;C. ;D. 
Câu 2: Trong các hình sau, hình nào khơng cĩ tâm đối xứng ? 
 A. Hình thang cân ; B. Hình bình hành ; 	C. Hình chữ nhật ; D. Hình thoi
Câu 3: Độ dài đường trung bình của hình thang là 16 cm ; hai đáy tỉ lệ với 3 và 5 thì độ dài hai đáy là :
 A.12 cm và 20 cm ; B. 6 cm và 10 cm ; C. 3 cm và 5 cm ; D. Đáp số khác 
Câu 4: Hình vuơng cĩ cạnh bằng 3dm thì đường chéo của hình vuơng bằng ?
 A. 18 dm	; B. 9 dm	 ; C. 6dm	 ; D. dm
Câu 5: Hãy điền vào chỗ (.) các cụm từ thích hợp để được câu đúng :
 a) Tam giác vuơng cĩ 2 cạnh gĩc vuơng là 6 cm và 8 cm thì độ dài đường trung tuyến ứng với cạnh huyền bằng 
 b) Tứ giác cĩ 2 cạnh đối bằng nhau và hai đường chéo bằng nhau thì nĩ là ..
II/ Phần tự luận:(7,0đ). 
Bài 1:(1,0đ). Cho tam giác ABC vuơng tại A, cĩ AB = 5cm ; BC = 13cm . Tính độ dài đường trung bình của tam giác song song với cạnh AC ?
Bài 2: (6,0đ).Cho hình bình hành ABCD cĩ AD = 2AB, . Gọi E, F lần lượt là trung điểm của BC và AD.
a) Chứng minh tứ giác AECF là hình bình hành.
b) Chứng minh AE BF
c) Tính 
d) Chứng minh tứ giác BFDC là hình thang cân.
e) Chứng minh E và D đối xứng với nhau qua FC. 
f) Chứng minh các đường thẳng AC, BD, EF cùng đi qua một điểm.
Trường THCS Hành Minh ĐÁP ÁN ĐỀ KIỂM TRA – HÌNH HỌC 8
GV : Lương Hữu Xuân Chủ đề : Tứ giác
ĐỀ 1:
I/ Phần trắc nghiệm: (3,0đ) Mỗi câu đúng 0,5đ
1
2
3
4
5a
5b
B
A
A
D
5cm
..h.thang cân
II/ Tự luận :(7,0đ)	
Bài
Câu
Nội dung đáp án
Điểm
Bài 1: (1,0đ)
-Tính đúng AC = 12cm 
-Tính đúng độ dài đường trung bình 
PQ = 6cm 
0,5đ
0,5đ
Bài 2: (6,0đ)
a)
.Vẽ hình đúng 
BC // AD và BC = AD CE // AF và CE = AF
Do đĩ Tứ giác AECF là hình bình hành	 
0,5đ
0,25đ
0,25đ
b)
.Ta cĩ AF // BE và AF = BE ABEF là hình bình hành
.Mà AB = AF (cùng bằng, do đĩ tứ giác ABEF là hình thoi
0,5đ
0,5đ
c)
Tính :
.Xét cĩ AB = AF và đều
. vuơng ở B. Do đĩ 
0,5đ
0,5đ
d)
.Tứ giác BFDC là hình thang ( Vì FD // BC)	 (1) .( 2 gĩc đối hình bình hành)	
Tính đúng 
Nên 	(2)	 
Từ (1) và (2) nên BFDC là hình thang cân 	
0,25đ
0,5đ
0,25đ
e)
.Chứng minh FC là trung trực của ED
.Suy ra E và D đối xứng qua FC
0,75đ
0,25đ
f)
Gọi O là giao đđiểm của hai đường chéo AC và BD
 O là trung điểm của AC O cũng là trung điểm của EF	
 Suy ra AC, BD, EF cùng đi qua O	 
0,5đ
0,5đ
 GVBM
 L­¬ng H÷u Xu©n
Trường THCS Hành Minh	 KIỂM TRA 1 TIẾT – HÌNH HỌC 8 / HKI
Họ và tên:	Chủ đề: Tứ giác
Lớp:	Thời gian: 45 ph
Điểm
Lời phê
Chữ ký của phụ huynh
ĐỀ 3:
I) Trắc nghiệm: (3đ).Chọn phương án đúng (Từ câu 1 – câu 3)
Câu 1:Các gĩc của tứ giác ABCD cĩ thì số đo các gĩc là :
A. B.;
C.; D.
Câu 2: Tứ giác nào vừa cĩ tâm đối xứng vừa cĩ hai trục đối xứng là hai đường chéo 
 A. Hình thang cân ; B. Hình bình hành ; 	C. Hình chữ nhật ; D. Hình thoi
Câu 3: Một hình thang cĩ 1 cặp gĩc đối là và . Cặp gĩc cịn lại là:
 A. 	 ; B. 	 ;C. 	 ;D. 
Câu 4: Hãy điền vào chỗ (.) các cụm từ thích hợp để được câu đúng :
 a) đều cĩ độ dài đường trung bình ứng với cạnh AB là 4 cm. Vậy chu vi tam giác là  ......cm.
 b) Hình thang cân cĩ hai đường chéo...................................................thì nĩ là hình chữ nhật.
 c) Hình thang cĩ 2 cạnh bên song song thì nĩ là hình.......................
II) Tự luận: (7,0đ).
Bài 1:(1,0đ). Cho tam giác ABC vuơng tại A, cĩ AC = 24cm ; BC = 26cm . Tính độ dài đường trung bình của tam giác song song với cạnh AB ?
Bài 1:(6,0đ). Cho tam giác ABC cân tại A cĩ , đường cao AM.Trên tia đối của tia MA lấy điểm E sao cho ME = MA. 
 a) Chứng minh tứ giác ABEC là hình thoi.
 b) Lấy điểm D đối xứng với E qua C. Đường thẳng qua E song song với BC cắt AC tại F. Tứ giác ADFE là hình gì ? Vì sao ?
 c) Chứng minh tứ giác ABEF là hình thang cân.
 d) Tứ giác ABCD là hình gì ? Vì sao ?
 e) Điểm C cĩ phải là trực tâm DDBF khơng ? Vì sao ?.
 f) Gọi I là giao điểm của BD và AM. Tính tỉ số ?
Trường THCS Hành Minh	 KIỂM TRA 1 TIẾT – HÌNH HỌC 8 / HKI
Họ và tên:	Chủ đề: Tứ giác
Lớp:	Thời gian: 45 ph
Điểm
Lời phê
Chữ ký của phụ huynh
ĐỀ 4
I) Trắc nghiệm: (3đ).Chọn phương án đúng (Từ câu 1 – câu 3)
Câu 1: Tứ giác ABCD cĩ :
A. ;B. ;C. ;D.
Câu 2: Tứ giác nào vừa cĩ tâm đối xứng vừa cĩ hai trục đối xứng là hai đường chéo 
 A. Hình thang cân ; B. Hình bình hành ; 	C. Hình chữ nhật ; D. Hình thoi
Câu 3: Một hình thang cĩ 1 cặp gĩc đối là và . Cặp gĩc cịn lại là:
 A. 	 ; B. 	 ;C. 	 ;D. 
Câu 4: Hãy điền vào chỗ (.) các cụm từ thích hợp để được câu đúng :
 a) Hình thang cĩ độ dài hai đáy là 8cm và 14cm thì độ dài đường trung bình là .........................cm 
 b) Tứ giác cĩ 2 đường chéo vuơng gĩc với nhau tạithì nĩ là hình thoi. 
 c) Hình thang cĩ 2 cạnh bên song song thì nĩ là hình.......................
II) Tự luận: (7,0đ).
Bài 1:(1,0đ). Cho tam giác ABC AB = 12cm cĩ AC = 24cm ; BC = 26cm . Gọi M, N, P lần lượt là trung điểm các cạnh AB, AC, BC.Tính chu vi tam giác MNP ?
Bài 1:(6,0đ). Cho hình chữ nhật ABCD cĩ O là giao điểm hai đường chéo. Lấy điểm E nằm giữa O và B. Gọi F là điểm đối xứng với A qua E, và I là trung điểm của CF.
 a) Chứng minh tứ giác ỊEFC là hình thang.
 b) Chứng minh tứ giác OEIC là hình bình hành
 c) Gọi H , K lần lượt là hình chiếu của F trên các đường thẳng BC và CD. Chứng minh tứ giác CHFK là hình chữ nhật.
 d) Chứng minh H và K đối xứng với nhau qua CF. 
 e) Chứng minh E, H, K thẳng hàng.
BÀI LÀM