Kiểm tra chất lượng đầu năm năm học: 2015-2016 môn thi: Toán - lớp 9

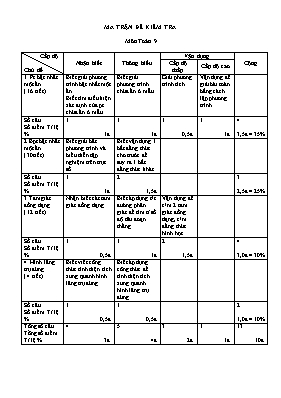
MA TRẬN ĐỀ KIỂM TRA
Môn Toán 9
 Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
1. Pt bậc nhất một ẩn. 
( 16 tiết )
Biết giải phương trình bậc nhất một ẩn.
Biết tìm điều kiện xác định của pt chứa ẩn ở mẫu
Biết giải phương trình chứa ẩn ở mẫu
Giải phương trình tích
Vận dụng để giải bài toán bằng cách lập phương trình
Số câu
Số điểm. Tỉ lệ %
1
 1đ
1
 1đ
1
 0,5đ
1
 1đ
4
3,5đ = 35%
2.Bpt bậc nhất một ẩn. 
( 30tiết)
Biết giải bất phương trình và biểu diễn tập nghiệm trên trục số
Biết vận dụng 1 bất đẳng thức cho trước để suy ra 1 bất đẳng thức khác
Số câu
Số điểm. Tỉ lệ %
1
 1đ
2
 1,5đ
3
2,5đ = 25%
3.Tam giác đồng dạng.
( 12 tiết )
Nhận biết các tam giác đồng dạng
Biết áp dụng t/c đường phân giác để tìm tỉ số độ dài đoạn thẳng
Vận dụng để c/m 2 tam giác đồng dạng, c/m đẳng thức hình học
Số câu
Số điểm. Tỉ lệ %
1
 0,5đ
1
 1đ
2
 1,5đ
4
3,0đ = 30%
4. Hình lăng trụ đứng.
( 4 tiết )
Biết viết công thức tính diện tích xung quanh hình lăng trụ đúng
Biết áp dụng công thức để tính diện tích xung quanh hình lăng trụ đứng
Số câu
Số điểm. Tỉ lệ %
1
 0,5đ
1
 0,5đ
2
1,0đ = 10%
Tổng số câu
Tổng số điểm. Tỉ lệ %
4
 3đ
5
 4đ
3
 2đ
1
 1đ
13
 10đ
Trường:...................................................
Họ tên:....................................................
Lớp: 9...
KIỂM TRA CHẤT LƯỢNG ĐẦU NĂM
Năm học: 2015-2016
Môn thi: TOÁN - Lớp 9
Thời gian: 90 phút (không kể thời gian phát đề)
ĐỀ SỐ 1:
Câu I: ( 2,5đ) Giải các phương trình sau
Câu II: ( 2,5đ )
 Giải và biểu diễn tập nghiệm của bất phương trình sau trên trục số : 
 Cho a < b so sánh
 3a và 3b	 - 2a +1 và - 2b + 1
Câu III: ( 1,0đ ) Giải bài toán sau bằng cách lập phương trình
	Lúc 5 giờ sáng, một canô xuôi dòng từ bến A đến bến B, rồi ngay lập tức từ bến B trở về A lúc 12 giờ cùng ngày. Tính khoảng cách từ bến A đến B, biết canô đến bến B lúc 8 giờ và vận tốc dòng nước là 3km/h.
Câu IV: ( 3,0đ ) 
	 Cho hình vẽ, tìm các cặp tam giác đồng dạng?
	 Cho tam giác ABC vuông tại A, có AB = 9cm, AC = 12cm, BC = 15cm, đường cao AH (HBC).
Chứng minh đồng dạng 
Chứng minh rằng 
Cho AD là đường phân giác của tam giác ABC (). Tính độ dài BD và DC. ( Làm tròn đến chữ số thập phân thứ nhất )
Câu V: ( 1,0đ ) 
	 Viết công thức tính diện tích xung quanh hình lăng trụ đứng. Giải thích kí hiệu.	 Tính diện tích xung quanh hình hộp chữ nhật ABCD.A’B’C’D’, biết AB = 5cm, AD = 8cm, AA’ = 12cm.Hết.
	HƯỚNG DẪN CHẤM BÀI
Câu
Nội dung
Điểm
I
(2,5đ)
1. 2x – 4 = 0 2x = 4 x = 2 
0,5 – 0,5
2. 3x2 – 6x = 0 3x( x- 2 ) = 0 3x = 0 hoặc x – 2 = 0 x = 0 hoặc x = 2 
0,25 – 0,25
3. có ĐKXĐ là và 
 2x = 3.(x -1 ) 2x = 3x – 3 2x – 3x = -3 x = 3
0,25 – 0,25
0,25 – 0,25
II
(2,5đ)
1. x– 5 > 0 x > 5 
0,5 – 0,5
2a. Ta có a < b 3a < 3b ( Nhân cả hai vế cho 3 )
0,5
2b. Ta có a - 2b -2a + 1 > -2b + 1
0,5 – 0,5
III
(1,0đ)
Gọi x ( km ) là quãng đường AB ( x > 0 ) 
Thời gian canô đi từ A đến B là 8 – 5 = 3 (h) 
Khi đó vận tốc của canô xuôi dòng là 
Thời gian canô ngược dòng là 12 – 8 = 4 (h)
Khi đó vận tốc ngược dòng là 
Do vận tốc dòng nước là 3km/h nên ta có phương trình
Giải phương trình ta có x = 72 ( thoả mãn điều kiện )
Vậy quãng đường AB dài 72 km
0,25
0,25
0,25
0,25
IV
(3,0đ)
1. DEF
0,5
2. 
2a. Xét và có:
 là góc chung
 Do đó 
0,5
0,5
2b. Do nên ta có : 
0,5 
2c. Vì AD là tia phân giác của nên ta có 
 9.(15 – x ) = 12x 135 – 9x = 12x
 21x = 135 x 6,4
Vậy : DB = 6,4 cm, DC = 15 – 6,4 = 8,6 cm 
0,25
0,25
0,25
0,25
V
(1,0đ)
1. p là nửa chu vi, h là chiều cao, S là diện tích xung quanh
0,25 – 0,25
2. = 2.( 5 + 8 ). 12 =312 (cm2)
0,25 – 0,25
Ghi chú:Học sinh làm cách khác lập luận chặt chẽ đạt điểm tối đa
Riêng câu IV.2: học sinh không vẽ hình không chấm điểm
 ĐỀ KIỂM TRA 
Môn: Toán 9 (Thời gian: 90 phút)
 MA TRẬN ĐỀ KIỂM TRA:
 Cấp độ
 Chủ đề 
Nhận biết
Thông hiểu
Vận dụng
 Cộng
Cấp độ thấp
Cấp độ cao
1. Phương trình chứa ẩn ở mẫu.
Biết tìm điều kiện xác định 
của của phương trình 
Giải được phương trình chứa ẩn ở mẫu
Số câu
Số điểm 
Tỉ lệ %
1 (1a) 
 1
10%
1 (1b)
 1
10%
2 
 2
20% 
2. Giải bài toán bằng cách lập phương trình.
Biểu diễn thành thạo mối liên hệ giữa các đại lượng s, t, v để lập phương trình
Số câu
Số điểm 
Tỉ lệ %
1 (C3)
 1
10%
1 
 1
10%
3. Bất phương trình bậc nhất một ẩn.
Biết giải bất phương trình bậc nhất một ẩn và biểu diễn tập nghiệm trên trục số.
Biết áp dụng các tính chất liên hệ giữa thứ tự với phép cộng, phép nhân để chứng minh bất đẳng thức
Số câu
Số điểm 
Tỉ lệ %
1(2a)
 1
10%
1(2b)
 1
10%
2
 2
20%
 4. Tam giác đổng dạng.
- Biết sử dụng ĐL Py-Ta-Go để tính độ dài cạnh của tam giác vuông.
- Biết áp dụng các trường hợp đồng dạng của tam giác vuông để chứng minh hai tam giác vuông đồng dạng
Biết áp dụng các kiến thức đã học để tính tỉ số diện tích của hai tam giác đồng dạng, tính độ dài đoạn thẳng.
Số câu
Số điểm
Tỉ lệ
2 (4a,4b)
 2
20%
2 (4c,4d)
 2
20%
4
 4
40%
5. Hình hộp chữ nhật
Tái hiện được công thức tính thể tích hình hộp chữ nhật; Tính được thể tích hình hộp chữ nhật.
Số câu
Số điểm
Tỉ lệ
2(5a,5b)
 1
 10%
2(5a,5b)
 1
 10%
Tổng số câu
Tổng số điểm
Tỉ lệ
4
 3
30%
4
 4
40% 
2
 2
20%
1
 1
10%
11
 10
100%
KIỂM TRA 
MÔN TOÁN- LỚP 9.
THỜI GIAN: 90 phút (không kể thời gian phát đề)
Câu 1: (2đ) Cho phương trình: 
 a/ Tìm điều kiện xác định của phương trình.
 b/ Giải phương trình trên.
Câu 2: (2đ) a/ Giải bất phương trình sau và biểu diễn tập nghiệm trên trục số:
 x + 2 0
 b/ Cho a>b, chứng minh: 4a + 3 > 4b + 3.
Câu 3: (1đ) Một người đi xe đạp từ A đến B với vận tốc trung bình 12km/h. Lúc về, người đó chỉ đi với vận tốc trung bình 10km/h, nên thời gian về nhiều hơn thời gian đi là 45 phút. Tính độ dài quãng đường AB?
Câu 4: (4đ) Cho tam giác ABC vuông tại A, có AB = 6cm, AC = 8cm, đường cao AH 
 ( H BC).
 a/ Tính độ dài BC.
 b/ Hãy chỉ ra các cặp tam giác đồng dạng (viết theo thứ tự các đỉnh tương ứng và giải thích vì sao chúng đồng dạng).
 c/ Tính tỉ số diện tích của hai tam giác HBA và HAC.
 d/ Cho AD là đường phân giác của góc BAC (D BC). Tính độ dài DB và DC
Câu 5: (1đ) a/ Viết công thức tính thể tích hình hộp chữ nhật.
 b/ Tính thể tích hình hộp chữ nhật ABCDA/B/C/D/ biết AB = 6cm, AA/ = 5cm,
AD = 4cm. Hết
ĐÁP ÁN 
MÔN TOÁN – Lớp 9
Câu 1 (2đ): a/ ĐKXĐ: x0 và x1 (1đ)
 b/ (1)
(1)3(x-1) = 2x
 3x – 3 = 2x
 3x – 2x = 3
 x = 3 (TMĐKXĐ)
Vậy phương trình có tập nghiệm là S = (1đ)
Câu 2 (2đ): a/ x + 2 0
 x -2
Vậy tập nghiệm của bất phương trình là (0,5đ)
 +Biểu diễn tập nghiệm trên trục số:
 -2 0 (0,5đ)
 b/ Nhân hai vế của bất phương trình a>b với 4 ta được: 
 4a>4b (0,5đ)
 Cộng 3 vào cả hai vế của bất phương trình này ta được:
 4a + 3 > 4b + 3 (0,5đ)
Câu 3 (1đ): Gọi độ dài quãng đường AB là x(km), điều kiện x>0 (0,25đ)
 Thời gian đi từ A đến B là: (h)
 Thời gian về từ B đến A là: (h) (0,25đ)
 Vì thời gian về nhiều hơn thời gian đi là 45 phút (45 phút = (h)) nên ta có phương trình: - = (0,25đ)
 6x – 5x = 45
 x = 45 (TMĐK)
 Vậy độ dài quãng đương AB là 45km. (0,25đ)
Câu 4 (4đ) Giám khảo tự vẽ hình.
 a/ Tính BC: Áp dụng định lý Py-Ta-Go vào tam giác vuông ABC ta có:
 BC2 = AB2 + AC2 
 BC2 = 62 + 82 = 100
 BC = 10(cm) (1d).
 b/ vABC đồng dạng vHBA (vì có góc B chung)
 vABC đồng dạng vHAC (vì có góc C chung)
 vHBA đồng dạng vHAC (vì có góc HAB = góc C do cùng phụ với góc B) (1đ).
 c/(1đ) Vì vHBA đồng dạng vHAC
 (SHBA) : (SHAC) = .
 d/ (1đ) Vì AD là đường phân giác của góc BAC. Áp dụng tính chất đường phân giác của tam giác, ta có:
 DB = 4,3
 DC = BC – BD = 10 – 4,3 = 5,7.
Câu 5 (1đ): a/ V = a.b.c, với a,b,c là các kích thước của hình hộp chữ nhật. (0,5đ)
 b/ V = AB.AD AA/ = 6.4.5 = 120 cm3. (0,5đ)