Kiểm tra 45 phút năm học 2015 - 2016 môn: Giải tích – lớp 11 tuần kiểm tra: 8

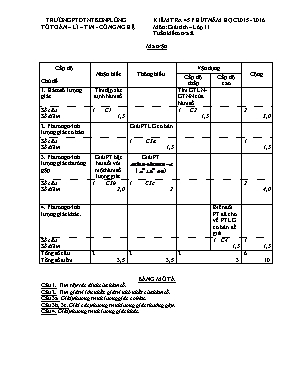
 TRƯỜNG PTDTNT KONPLÔNG 
TỔ TOÁN – LÍ – TIN - CÔNG NGHỆ
KIỂM TRA 45 PHÚT NĂM HỌC 2015 - 2016
Môn: Giải tích – Lớp 11
Tuần kiểm tra: 8
Ma trận
Cấp độ
Chủ đề 
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
1. Hàm số lượng giác
Tìm tập xác định hàm số
Tìm GTLN-GTNN của hàm số
Số câu 
Số điểm 
1 C1
1,5 
1 C2
1,5 
2
3,0 
2. Phương trình lượng giác cơ bản
Giải PTLG cơ bản
Số câu 
Số điểm 
1 C3a
1,5 
1
1,5 
3. Phương trình lượng giác thường gặp
Giải PT bậc hai đối với một hàm số lượng giác
Giải PT 
()
Số câu 
Số điểm 
1 C3b
2,0 
1 C3c
2 
2
4,0 
4. Phương trình lượng giác khác.
Biến đổi PT đã cho về PTLG cơ bản để giải
Số câu 
Số điểm 
1 C4
1,5 
1
1,5 
Tổng số câu 
Tổng số điểm 
2	
3,5
2
3,5
2
3
6
10
BẢNG MÔ TẢ
Câu 1. Tìm tập xác định của hàm số. 
Câu 2. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số.
Câu 3a. Giải phương trình lượng giác cơ bản.
Câu 3b, 3c. Giải các phương trình lượng giác thường gặp.
Câu 4. Giải phương trình lượng giác khác.
 TRƯỜNG PTDTNT KONPLÔNG 
TỔ TOÁN – LÍ – TIN - CÔNG NGHỆ
KIỂM TRA 45 PHÚT NĂM HỌC 2015 - 2016
Môn: Giải tích – Lớp 11
Tuần kiểm tra: 8
Đề bài
Câu 1 (1,5đ): Tìm tập xác định của hàm số: 
Câu 2 (1,5đ): Tìm giá trị lớn nhất của hàm số: 
Câu 3 (5,5đ): Giải các phương trình lượng giác sau:
 	 a) ;	
b) ;
c) ;	
Câu 4 (1,5đ): Giải các phương trình lượng giác sau:
.
 TRƯỜNG PTDTNT KONPLÔNG 
TỔ TOÁN – LÍ – TIN - CÔNG NGHỆ
KIỂM TRA 45 PHÚT NĂM HỌC 2015 - 2016
Môn: Giải tích – Lớp 11
Tuần kiểm tra: 8
Hướng dẫn chấm
Câu
Ý
Đáp án
Điểm
1
Hàm số xác định khi và chỉ khi
TXĐ: 
0,75
0,75
2
 Hàm số đạt giá trị lớn nhất khi và chỉ khi đạt giá trị nhỏ nhất.
Ta có: suy ra min 
Vậy 
0,5
0,5
0,5
3
a
0,5
0,75
0,25
b
Đặt , điều kiện . Phương trình trở thành:
Với , ta có: 
Vậy phương trình đã cho có nghiệm 
0,5
0,75
0,75
c
0,5
0,5
0,5
0,5
4
ĐK: 
0,5
0,5
0,25
0,25
KonPLông, ngày tháng năm 2015
DUYỆT CỦA TỔ CUYÊN MÔN GIÁO VIÊN RA ĐỀ
DUYỆT CỦA CHUYÊN MÔN NHÀ TRƯỜNG