Kiểm tra 1 tiết - Năm học 2016 - 2017 môn: Hình học 12 - Đề 01

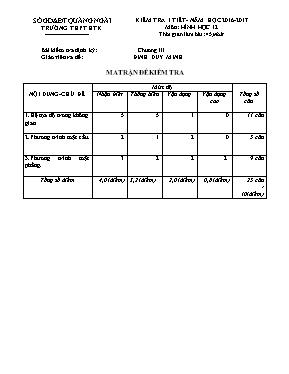
SỞ GD&ĐT QUÃNG NGÃI
TRƯỜNG THPT HTK
KIỂM TRA 1 TIẾT- NĂM HỌC 2016-2017
Môn: HÌNH HỌC 12
Thời gian làm bài: 45 phút
Bài kiểm tra định kỳ: 	 Chương III
Giáo viên ra đề: 	 ĐINH DUY MINH
MA TRẬN ĐỀ KIỂM TRA
NỘI DUNG-CHỦ ĐỀ
Mức độ
Tổng số
câu
Nhận biết
Thông hiểu
Vận dụng
Vận dụng 
cao
1.Hệ tọa độ trong không gian
5
 5
1
0
11 câu
2.Phương trình mặt cầu.
2
 1
2
0
5 câu
3.Phương trình mặt phẳng.
3
2
2
 2
9 câu
Tổng số điểm
4,0 (điểm)
3,2 (điểm)
2,0 (điểm)
0,8 (điểm)
25 câu
/ 
10(điểm)
SỞ GD&ĐT THỪA THIÊN HUẾ
TRƯỜNG THPT PHONG ĐIỀN
KIỂM TRA ĐỊNH KÌ- NĂM HỌC 2012- 2013
Môn: HÌNH HỌC 12 (NC)
Thời gian làm bài: 45 phút 
 ĐỀ CHÍNH THỨC
ĐỀ 01
ĐỀ KIỂM TRA 1 TIẾT 
Môn: HÌNH HỌC 12 (Nâng cao) Thời gian: 45 phút 
---------------
Câu 1 (4,0 điểm): Cho ba điểm , , .
(1,0 điểm) Chứng minh: A, B, C là ba đỉnh của một tam giác.
(1,0 điểm) Xác định tọa độ điểm D sao cho ABCD là hình bình hành.
(1,0 điểm) Viết phương trình mặt phẳng (ABC).
(1,0 điểm) Viết phương trình mặt cầu có đường kính AB.
Câu 2 (4,0 điểm): Cho điểm và d:
	a) (2,0 điểm) Xác định tọa độ hình chiếu vuông góc của A trên đường thẳng d.
	b) (2,0 điểm) Viết phương trình đường thẳng ∆ đi qua điểm A, cắt và vuông góc với đường thẳng d.
Câu 3 (2,0 điểm): Cho đường thẳng , mặt phẳng (P): và điểm . Viết phương trình đường thẳng cắt và (P) lần lượt tại M và N sao cho A là trung điểm của đoạn MN.
-----Hết-----
ĐỀ 02
ĐỀ KIỂM TRA 1 TIẾT 
Môn: HÌNH HỌC 12 (Nâng cao) Thời gian: 45 phút 
---------------
Câu 1 (4,0 điểm): Cho ba điểm , , .
(1,0 điểm) Chứng minh: A, B, C là ba đỉnh của một tam giác.
(1,0 điểm) Xác định tọa độ điểm D sao cho: .
(1,0 điểm) Viết phương trình mặt phẳng (ABC).
(1,0 điểm) Viết phương trình mặt cầu có đường kính AC.
Câu 2 (4,0 điểm): Cho điểm và mặt phẳng (P): 
	a) (2,0 điểm) Xác định tọa độ hình chiếu vuông góc của A trên mặt phẳng (P).
	b) (2,0 điểm) Viết phương trình mặt cầu (S) có tâm A, biết mặt cầu (S) cắt mặt phẳng (P) theo thiết diện là một đường tròn có chu vi 
Câu 3 (2,0 điểm): Cho điểm , mặt phẳng và đường thẳng . Viết phương trình đường thẳng đi qua điểm A, cắt tại B và cắt (P) tại C sao cho .
-----Hết-----
SỞ GD&ĐT THỪA THIÊN HUẾ
TRƯỜNG THPT PHONG ĐIỀN
KIỂM TRA ĐỊNH KÌ- NĂM HỌC 2012- 2013
Môn: HÌNH HỌC 12 (NC)
Thời gian làm bài: 45 phút 
ĐỀ 01
 ĐÁP ÁN CHÍNH THỨC
 (có 02 trang)
ĐÁP ÁN – THANG ĐIỂM
Câu
Nội dung
Điểm
1
a) , , .
Ta có: 
Do và không cùng phương
A, B, C không thẳng hàng (đ.p.c.m)
0,25
0,25
0,25
0,25
b) Gọi là điểm cần tìm.
Ta có: và 
Tứ giác ABCD là hình bình hành
0,25
0,25
0,25
0,25
c) Ta có: 
Mặt phẳng (ABC) đi qua và có 1 vtp là 
(ABC): 
0,25
0,25
0,25
0,25
d) Tâm I của mặt cầu cần tìm là trung điểm AB
Ta có: 
Bán kính mặt cầu là: 
Vậy phương trình (S): 
0,25
0,25
0,25
0,25
2
a) Gọi 
Đường thẳng d có 1 vectơ chỉ phương 
H là hình chiếu của A trên d
1,0
1,0
b) Đường thẳng cần tìm là đường thẳng qua và có 1 vectơ chỉ phương .
0,5
0,5
0,5
0,5
3
Ta có: . Gọi 
Do A là trung điểm của MN, suy ra .
Mặt khác: .
Đường thẳng đi qua A và M có phương trình: .
0,5
0,5
0,5
0,5
Lưu ý: Học sinh làm cách khác đúng vẫn cho điểm tối đa.
SỞ GD&ĐT THỪA THIÊN HUẾ
TRƯỜNG THPT PHONG ĐIỀN
KIỂM TRA ĐỊNH KÌ- NĂM HỌC 2012- 2013
Môn: HÌNH HỌC 12 (NC)
Thời gian làm bài: 45 phút 
ĐỀ 02
 ĐÁP ÁN CHÍNH THỨC
 (có 02 trang)
ĐÁP ÁN – THANG ĐIỂM
Câu
Nội dung
Điểm
1
a), , 
Ta có: 
Do và không cùng phương
A, B, C không thẳng hàng (đ.p.c.m)
0,25
0,25
0,25
0,25
b) Gọi là điểm cần tìm.
Ta có: và 
Theo giả thiết 
0,25
0,25
0,25
0,25
c) Ta có: 
Mặt phẳng (ABC) đi qua và có 1 vtp là 
(ABC): 
0,25
0,25
0,25
0,25
d) Tâm I của mặt cầu cần tìm là trung điểm AC
Ta có: 
Bán kính mặt cầu là: 
Vậy phương trình (S): 
0,25
0,25
0,25
0,25
2
a) Mặt phẳng (P) có 1 vectơ pháp tuyến 
Đường thẳng d qua và vuông góc với mặt phẳng (P) nên d nhận làm 1 vectơ chỉ phương:
d: 
Tọa độ H là nghiệm của hệ phương trình 
Thay (1), (2), (3) vào (4) ta có phương trình:
1,0
1,0
b) 
Gọi là bán kính mặt cầu (S) cần tìm và là bán kính đường tròn giao tuyến của (P) và (S).
Theo giả thiết: và 
Ta có: 
Vậy (S): (y.c.b.t)
0,5
0,5
0,5
0,5
3
Gọi 
Ta có: 
Theo giả thiết: 
Đường thẳng qua và có 1 vectơ chỉ phương 
 : 
0,5
0,5
0,5
0,5
Lưu ý: Học sinh làm cách khác đúng vẫn cho điểm tối đa.