Kiểm tra 1 tiết môn: Đại số và giải tích 11 (tiết 62)

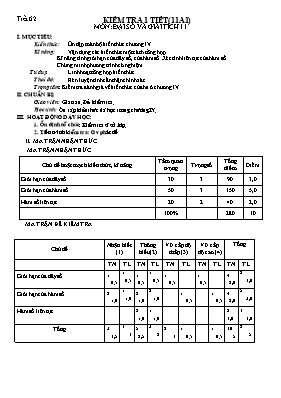
Tiết 62	 KIỂM TRA 1 TIẾT(11A1)
MƠN: ĐẠI SỐ VÀ GIẢI TÍCH 11
I. MỤC TIÊU:
	Kiến thức:	Ơn tập tồn bộ kiến thức chương IV.
	Kĩ năng:	Vận dụng các kiến thức một cách tổng hợp.
Kĩ năng tính giới hạn của dãy số, của hàm số. Xét tính liên tục của hàm số.
Chứng minh phương trình cĩ nghiệm.
Tư duy:	Linh hoạt tổng hợp kiến thức
	Thái độ:	Rèn luyện tính cẩn thận chính xác.
	Trọng tâm: Kiểm tra đánh giá về kiến thức của hs ở chương IV
II. CHUẨN BỊ:
Giáo viên: Giáo án. Đề kiểm tra.
	Học sinh: Ôn tập kiến thức đã học trong chương IV.
III. HOẠT ĐỘNG DẠY HỌC:
	1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
	2. Tiến trình kiểm tra: Gv phát đề
II. MA TRẬN NHẬN THỨC
 MA TRẬN NHẬN THỨC
Chủ đề hoặc mạch kiến thức, kĩ năng
Tầm quan trọng
Trọng số
Tổng điểm
Điểm
Giới hạn của dãy số
30
3
90
3,0
Giới hạn của hàm số
50
3
150
5,0
Hàm số liên tục
20
2
40
2,0
100%
280
10
MA TRẬN ĐỀ KIỂM TRA
Chủ đề
Nhận biết (1)
Thơng hiểu (2)
VD cấp độ thấp (3)
VD cấp độ cao (4)
Tổng
TN
TL
TN
TL
TN
TL
TN
TL
TN
TL
Giới hạn của dãy số
1
0,5
1
0,5
1 
0,5
1
0,5
1
0,5
1
0,5
4
2,0
2
1,0
Giới hạn của hàm số
2
1,0
1
1,0
2
1,0
2
1,0
1
0,5
1
0,5
4
2,0
5
3,0
Hàm số liên tục
2
1,0
1
1,0
2
1,0
1
1,0
Tổng
3
1,5
1
1
5
2,5
3
2
2
1
1 
0,5
1
0,5
10
5
8
5
BẢNG MƠ TẢ TIÊU CHÍ LỰA CHỌN CÂU HỎI TRẮC NGHIỆM
BẢNG MƠ TẢ CHI TIẾT NỘI DUNG CÂU HỎI ĐỀ KIỂM TRA
CHỦ ĐỀ : ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
CHỦ ĐỀ
CÂU
MƠ TẢ
1. Giới hạn của dãy số
Trắc nghiệm
1
Nhận biết: Giới hạn của dãy số.
2
Tơng hiểu: Giới hạn của dãy số.
3
Vận dụng: Áp dụng tổng của cấp số nhân để tính giới hạn của dãy số
10
Vận dụng cao: Tách biểu thức tính giới hạn
Tự luận
1a
Nhận biết: Giới hạn của dãy số.
1b
Thơng hiểu: Giới hạn của dãy số
2. Giới hạn của hàm số
Trắc nghiệm
4
Nhận biết: Giới hạn của hàm số.
5
Thơng hiểu: Giới hạn của hàm số.
6
Thơng hiểu: Giới hạn của hàm số.
7
Vận dụng: Giới hạn của hàm số.
Tự luận
2a
Thơng hiểu: Giới hạn của hàm số.
2b
Thơng hiểu: Giới hạn của hàm số.
2c
Vận dụng: Giới hạn của hàm số.
2d
Vận dụng cao: Giới hạn của hàm số.
2e
Vận dụng cao: Giới hạn của hàm số.
3. Hàm số liên tục
Trắc nghiệm
10
Thơng hiểu: Phương trình cĩ nghiệm
11
Thơng hiểu: Hàm số liên tục tại 1 điểm
Tự luận
3
Thơng hiểu: Hàm số liên tục
TRẮC NGHIỆM KHÁCH QUAN
Câu 1: Tìm ta được: A. 	B. -10	 	 C. 	D. 
Câu 2: Tìm ta được: A. 	B. 	 C. 	 D. 
Câu 3: Tìm ta được: A. 	B. C. D. 
Câu 4: Tìm ta được: A. 	B. 	 C. 5 	 D. 
Câu 5: Tìm , thì 4a+1= A. -2 	 B. -3 	 C. 1/4 D. 
Câu 6: Tìm ta được A. 	B. 	 C. D. 
Câu 7: Tìm ta được: A. 	 B. 	 C. D. 0
Câu 8: Phương trình cĩ ít nhất 1 nghiệm trong khoảng (-1;1) khi:
 A. 	B. 	C. m-1	D. 
Câu 9: Cho hàm số: để f(x) liên tục tại x=1 thì m bằng?
A. 1/2	B. -1	C. 2	D. 1
Câu 10: Cho . Khi đĩ bằng :
 	 A. 	B. 1/2 	C. 3/4 	D. 1/3 
II. TỰ LUẬN
Bài 1(1 điểm). Tính giới hạn của các dãy số sau:
; b) 
Bài 2(3 điểm). Tính giới hạn của các hàm số sau:
 a) b) c); 
 d) e) 
Bài 3(1 điểm).Xác định m để hàm số f(x) liên tục trên R, với 
ĐÁP ÁN:
TRẮC NGHIỆM: 
1
2
3
4
5
6
7
8
9
10
C
C
B
C
A
A
B
C
B
B
TỰ LUẬN:
Câu 
Hướng dẫn
Điểm
1a
0,5đ 
1b
0,5đ
2a
0,5đ
2b
0,5đ
2c
0,5đ
2d
0,5đ
2e
0,5đ
3
+) Với x<-1, ta cĩ , suy ra HS f(x) liên tục trên 
+) Với x>-1, ta cĩ suy ra HS f(x) liên tục trên 
0,5đ
Vậy hàm số f(x) liên tục trên R khi và chỉ khi nĩ liên tục tại x= -1
Hàm số f(x) liên tục tại x= -1. Tìm được m=-6
0,5đ