Kiểm tra 1 tiết giải tích chương 3 (Mã đề 255)

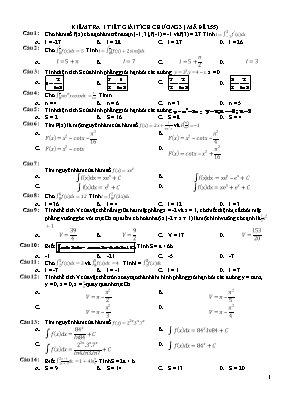
KIỂM TRA 1 TIẾT GIẢI TÍCH CHƯƠNG 3 ( MÃ ĐỀ 255)
C©u 1 : 
Cho hàm số f(x) có đạo hàm trên đoạn [-1 ;3], f(-1) = -1 và f(3) = 27. Tính I=-13f'xdx
A.
I = -27
B.
I = 28
C.
I = 27
D.
I = 26
C©u 2 : 
Cho 0π2fxdx=5. Tính I=0π2fx+2sinxdx
A.
I=5+π
B.
I=7
C.
I=5+π2
D.
I=3
C©u 3 : 
Tính diện tích S của hình phẳng giới hạn bởi các đường y=3x,y=4-x. x = 0.
A.
B.
C.
D.
C©u 4 : 
Cho 0π6sinnxcosxdx=164. Tìm n
A.
n = 4
B.
n = 6
C.
n = 3
D.
n = 5
C©u 5 : 
Tính diện tích S của hình phẳng giới hạn bởi các đường.
A.
S = 2
B.
S = 16
C.
S = 8
D.
S = 4
C©u 6 : 
Tìm F(x) là một nguyên hàm của hàm số fx=2x+1sin2x và Fπ4=-1
A.
Fx=x2-cotx-π216
B.
Fx=x2-cotx-π24
C.
Fx=x2-cotx
D.
Fx=cotx-x2+π216
C©u 7 : 
Tìm nguyên hàm của hàm số fx=xex
A.
fxdx=xex+C
B.
fxdx=xex-ex+C
C.
fxdx=ex+C
D.
fxdx=xex+ex+C
C©u 8 : 
Cho 06fxdx=12. Tính I=02f3xdx
A.
I = 36
B.
I = 4
C.
I = 12
D.
I = 3
C©u 9 : 
Tính thể tích V của vật thể nằm giữa hai mặt phẳng x = -2 và x = 1, có thiết diện bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (-2 ≤ x ≤ 1) là một hình vuông có cạnh là 12x2+1
A.
V=394
B.
V=92
C.
V = 17
D.
V=15320
C©u 10 : 
Biết , Tính S = a + 6b
A.
-1
B.
-21
C.
-5
D.
-7
C©u 11 : 
Cho 25fxdx=3 và 85fxdx=4 . Tính I = 28fxdx
A.
I = -7
B.
I = -1
C.
I = 1
D.
I = 7
C©u 12 : 
Tính thể tích V của vật thể tròn xoay tạo thành khi hình phẳng giới hạn bởi các đường y = tanx, 
y = 0, x = 0, x = π4 quay quanh trục Ox. 
A.
V=π-π22
B.
V=π-π25
C.
V=π-π23
D.
V=π-π24
C©u 13 : 
Tìm nguyên hàm của hàm số fx=22x.3x.7x
A.
fxdx=84xln84+C
B.
fxdx=84x.ln84+C
C.
fxdx=22x.3x.7xln4.ln3.ln7+C
D.
fxdx=84x+C
C©u 14 : 
Biết 12x-1x+3dx=1+4lnab. Tính S = 2a + b
A.
S = 9
B.
S = 14
C.
S = 13
D.
S = 20
C©u 15 : 
Tìm nguyên hàm của hàm số fx=x32-x2
A.
fxdx=-13(x2+4)2-x2+C
B.
fxdx=x2-x2+C
C.
fxdx=-13x22-x2+C
D.
fxdx=-13(x2-4)2-x2+C
C©u 16 : 
Tính diện tích S của hình phẳng giới hạn bởi hai đường và 
A.
S = 
B.
S = 
C.
S=e2+2
D.
S = 
C©u 17 : 
Cho hàm số y = f(x) có nguyên hàm trên đoạn [a ;b] và f(a) = f(b). Mệnh đề nào dưới đây đúng ?
A.
abf'xefxdx=2
B.
abf'xefxdx=1
C.
abf'xefxdx=-1
D.
abf'xefxdx=0
C©u 18 : 
Tính thể tích V của vật thể tròn xoay tạo thành khi hình phẳng giới hạn bởi các đường vàquay quanh trục Ox. 
A.
V=4π5
B.
V=3π5
C.
V=3π4
D.
V=4π3
C©u 19 : 
Biết F(x) là một nguyên hàm của hàm số fx=xx2-3 và F(2) = 1. Tính F(3)
A.
F3=12ln6+1
B.
F3=12ln6
C.
F3=ln6+1
D.
F3=12ln6-1
C©u 20 : 
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm sốvà trục Ox. Số nguyên lớn nhất không vượt quá S là:
A.
27
B.
10
C.
6
D.
7
Họ và tên:..
Lớp:.
SỐ CÂU ĐÚNG
ĐIỂM
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
phiÕu soi - ®¸p ¸n (Dµnh cho gi¸m kh¶o)
M«n : DE KTGT CHUONG 3 (2)
M· ®Ò : 255
01
{ ) } ~
02
{ ) } ~
03
{ | ) ~
04
{ | ) ~
05
{ | ) ~
06
) | } ~
07
{ ) } ~
08
{ ) } ~
09
{ | } )
10
) | } ~
11
{ ) } ~
12
{ | } )
13
) | } ~
14
{ | ) ~
15
) | } ~
16
{ | } )
17
{ | } )
18
{ | } )
19
) | } ~
20
{ | ) ~