Kiểm tra 1 tiết giải tích chương 1 môn: Toán 12

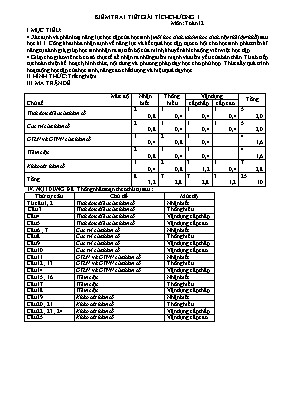
KIỂM TRA 1 TIẾT GIẢI TÍCH CHƯƠNG 1
	Môn: Toán 12
I. MỤC TIÊU:
· Xác định và phân loại năng lực học tập của học sinh (mỗi học sinh, nhóm học sinh, tập thể lớp/khối) sau học kì 1. Công khai hóa nhận định về năng lực và kết quả học tập, tạo cơ hội cho học sinh phát triển kĩ năng tự đánh giá, giúp học sinh nhận ra sự tiến bộ của mình, khuyến khích động viên việc học tập.
· Giúp cho giáo viên có cơ sở thực tế để nhận ra những điểm mạnh và điểm yếu của bản thân. Từ đó tiếp tục hoàn thiện kế hoạch, hình thức, nội dung và phương pháp dạy học cho phù hợp. Thúc đẩy quá trình hoạt động học tập của học sinh, nâng cao chất lượng và hiệu quả dạy học.
II. HÌNH THỨC: Trắc nghiệm.
III. MA TRẬN ĐỀ.
Mức độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Tổng
cấp thấp
cấp cao
Tính đơn điệu của hàm số
2
0,8
1
0,4
1
0,4
1
0,4
5
2,0
Cực trị của hàm số
2
0,8
1
0,4
1
0,4
1
0,4
5
2,0
GTLN và GTNN của hàm số
1
0,4
2
0,8
1
0,4
4
1,6
Tiệm cận
2
0,8
1
0,4
1
0,4
4
1,6
Khảo sát hàm số
1
0,4
2
0,8
3
1,2
1
0,4
7
2,8
Tổng
8
3,2
7
2,8
7
2,8
3
1,2
25
10
IV. NỘI DUNG ĐỀ. Thống nhất soạn theo thứ tự sau :
Thứ tự câu
Chủ đề
Mức độ
Từ câu 1, 2
Tính đơn điệu của hàm số
Nhận biết
 Câu 3
Tính đơn điệu của hàm số
Thông hiểu
Câu 4
Tính đơn điệu của hàm số
Vận dụng cấp thấp
Câu 5
Tính đơn điệu của hàm số
Vận dụng cấp cao
Câu 6 ; 7
Cực trị của hàm số
Nhận biết
Câu 8
Cực trị của hàm số
Thông hiểu
Câu 9
Cực trị của hàm số
Vận dụng cấp thấp
Câu 10
Cực trị của hàm số
Vận dụng cấp cao
Câu 11
GTLN và GTNN của hàm số
Nhận biết
Câu 12 ; 13
GTLN và GTNN của hàm số
Thông hiểu
Câu 14
GTLN và GTNN của hàm số
Vận dụng cấp thấp
Câu 15 ; 16
Tiệm cận
Nhận biết
Câu 17
Tiệm cận
Thông hiểu
Câu 18
Tiệm cận
Vận dụng cấp thấp
Câu 19
Khảo sát hàm số
Nhận biết
Câu 20 ; 21
Khảo sát hàm số
Thông hiểu
Câu 22 ; 23 ; 24 
Khảo sát hàm số
Vận dụng cấp thấp
Câu 25
Khảo sát hàm số
Vận dụng cấp cao
ĐỀ BÀI
Câu 1. Cho hàm số . Khẳng định nào sau đây đúng?
A. Hàm số luôn nghịch biến trên .
B. Hàm số luôn đồng biến trên .
C. Hàm số nghịch biến trên các khoảng (–¥; –1) và (–1; +¥).
D. Hàm số đồng biến trên các khoảng (–¥; –1) và (–1; +¥).
Câu 2. Trong các hàm số sau,hàm số nào luôn luôn đồng biến trên khoảng
A. B. C. D. 
Câu 3: Cho hàm số . Khẳng định nào sau đây đúng?
A.Hàm số đồng biến trên các khoảng .
B.Hàm số nghịch biến trên khoảng .
C.Hàm số đồng biến trên khoảng .
D.Hàm số nghịch biến trên các khoảng và .
Câu 4. Tìm tất cả các giá trị của tham số thực m để hàm số đồng biến trên ?
	A. hoặc 	B. 	C. 	D. 
Câu 5. Tìm tất cả các giá trị của tham số thực m hàm số đồng biến trên khoảng .
A. m > 1.	B. –1 1.
Câu 6. Đồ thi hàm số nào sau đây có 3 điểm cực trị ? 
A. 	B. 	C. 	D. 
Câu 7. Tìm tọa độ điểm cực tiểu của đồ thị hàm số ?
A. ( 1 ; 3 )	B. ( -1 ; 3 )	C. ( -1 ; 1 )	D. ( 1 ; -1 )
Câu 8. Tìm tất cả các giá trị của tham số thực m để hàm số đạt cực tiểu tại x = 2?
A. 	B. 	C. 	D. 
Câu 9. Cho đồ thị hàm số có một điểm cực trị là (1; 2). Tính khoảng cách giữa điểm cực tiểu và điểm cực đại?
A. 	 	B. 	C. 	D. 2
Câu 10. Tính tổng các giá trị của m để hàm số đạt cực trị tại thỏa mãn ?
A. -7 B. – 5 C. – 3 D. – 1 
Câu 11. Cho hàm số . Khẳng định náo sau đây đúng?
A. Hàm số có giá trị lớn nhất và có giá trị nhỏ nhất ; 
B. Hàm số có giá trị nhỏ nhất và không có giá trị lớn nhất ;	
C. Hàm số có giá trị lớn nhất và không có giá trị nhỏ nhất ;	
D. Hàm số không có giá trị lớn nhất và giá trị nhỏ nhất.
Câu 12. Tìm x để hàm số đạt giá trị lớn nhất? 
 B. C. D. 
Câu 13. Gọi M, m lần lượt là GTLN, GTNN của hàm số: trên . 
Tính tổng M + m?
A. 2	B. -4	C. 0	D. -2
Câu 14: Người ta giới thiệu một loại thuốc kích thích sự sinh sản của một loại vi khuẩn. Sau t phút , số vi khuẩn được xác định theo công thức . Hỏi sau bao nhiêu phút thì số vi khuẩn lớn nhất?
A.10 phút B.20 phút C.25 phút D.30 phút 
Câu 15. Tìm các tiệm của đồ thị hàm số .
A. Tiệm cận đứng x = 0, tiệm cận ngang y = -2
B. Tiệm cận đứng x = 0, tiệm cận ngang y = 2.
C. Tiệm cận đứng x = -2, tiệm cận ngang y = 2.
D. Tiệm cận đứng x = -2, tiệm cận ngang y = 0.
Câu 16. Cho hàm số . Tìm tiệm cận ngang của đồ thị hàm số?
A. y = 0 B. Không có tiệm cận ngang. C. 	 D. 
Câu 17. Cho hàm số: . Khẳng định nào sau đây sai?
A. Hàm số có tiệm cận đứng là x = 3	
B. Đồ thị hàm số có tiệm cận ngang là y = 0
C. Đồ thị hàm số có ba đường tiệm cận
D. Đồ thị hàm số có hai tiệm cận đứng
Câu 18. Cho hàm số: . Tìm các giá trị của tham số m để đồ thị hàm số có ba đường tiệm cận?
A. B. C. và D. 
Câu 19. Đồ thị dưới đây là đồ thị của hàm số nào? 
A. 	B. 
C. 	D. 
Câu 20. Đồ thị hàm số nào sau đây cắt trục tung tại điểm có tung độ âm?
A. y = .	B. y = .	C. y = .	D. y = .
Câu 21. Cho hàm số . Tìm tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng 2? 
A.	 B. C. 	 D. 
Câu 22. Tìm số giao điểm của đường cong y = x3 – 2x2 + 2x + 1 và đường thẳng y = 1 – x?
A. 0.	B.2.	C.3.	D.1.
Câu 23. Cho hàm số có đồ thị (C). Tìm tất cá các giá trị của tham số m để đường thẳng cắt đồ thị (C) tại hai điểm phân biệt M và N sao cho độ dài đoạn thẳng MN nhỏ nhất ?
 B. C. D. 
Câu 24 : Tìm các giá trị của tham số m để phương trình có nghiệm?
A. B. C. D. 
Câu 25. Cho hàm số . Tiếp tuyến bất kì của đồ thị hàm số cắt hai tiệm cận lần lượt tại hai điểm A và B. Gọi I là giao 2 đường tiệm cận. Tính diện tích tam giác IAB ?
1
2
5
D. 6
Đáp án:
1
D
6
C
11
A
16
A
21
A
2
B
7
D
12
C
17
A
22
D
3
C
8
A
13
B
18
C
23
A
4
A
9
C
14
B
19
A
24
C
5
A
10
A
15
C
20
B
25
D