Hình học lớp 8 - Tiết 55: Kiểm tra chương III

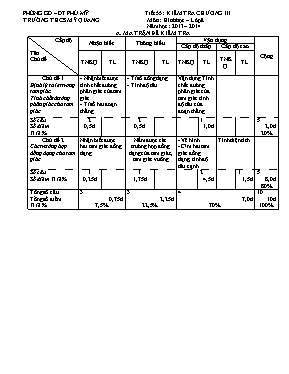
PHÒNG GD – ĐT PHÙ MỸ	 Tiết 55: KIỂM TRA CHƯƠNG III
TRƯỜNG THCS MỸ QUANG	 Môn : Hình học – Lớp 8 
 Năm học: 2013 – 2014 
A. MA TRẬN ĐỀ KIỂM TRA
 Cấp độ
Tên 
Chủ đề 
Nhận biết
Thông hiểu
Vận dụng
Cộng
 Cấp độ thấp
Cấp độ cao
TNKQ
TL
TNKQ
TL
TNKQ
TL
TNKQ
TL
Chủ đề 1 
Định lý ta let trong tam giác. 
Tính chất đường phân giác của tam giác
- Nhận biết được tính chất đường phân giác của tam giác
- Tỉ số hai đoạn thẳng
- Tỉ số đồng dạng
- Tính độ dài
Vận dụng Tính chất đường phân giác của tam giác tính độ dài của đoạn thẳng
Số câu 
Số điểm 
Tỉ lệ %
2
0,5đ
2
0,5đ
1
1,0đ
5
2,0đ 
20%
Chủ đề 2
Các trường hợp đồng dạng của tam giác
Nhận biết được hai tam giác đồng dạng
Nắm được các trường hợp đồng dạng của tam giác, tam giác vuông
- Vẽ hình
- C/m hai tam giác đồng dạng, tính độ dài cạnh
Tính diện tích
Số câu 
Số điểm Tỉ lệ %
1
0,25đ
1
1,75đ
2
4,5đ
1
1,5đ
5
8,0đ 
80%
Tổng số câu 
Tổng số điểm
Tỉ lệ %
3
0,75đ
7,5%
3
2,25đ
22,5%
4
7,0đ
70%
10
10đ 
100%
B. ĐỀ BÀI 
I TRẮC NGHIỆM: ( 3 điểm) 
Khoanh tròn chữ cái đứng trước câu trả lời đúng
Câu 1: Cho đoạn thẳng AB = 20cm, CD = 30cm. Tỉ số của hai đoạn thẳng AB và CD là:
	A. 	B. 	C. 	D. 	
Câu 2: Cho AD là tia phân giác ( hình vẽ) thì: 
	A. 	B. 	 C. 	D. 
Câu 3: Cho ABC DEF theo tỉ số đồng dạng là thì DEF ABC theo tỉ số đồng dạng là:
	A. 	B. 	C. 	D. 
Câu 4: Độ dài x trong hình vẽ là: (DE // BC)
	A. 5	B. 6
	C.7	D.8
Câu 5: Nếu hai tam giác ABC và DEF có và thì : 
	A. ABC DEF	 B. ABC DFE C.CAB DEF 	 D. CBA DFE
Câu 6: Điền dấu “X” vào ô trống thích hợp
Câu
Đ
S
1. Hai tam giác đồng dạng thì bằng nhau
2. Hai tam giác vuông cân luôn đồng dạng
3. Tỉ số chu vi của hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng
4. Hai tam giác bằng nhau thì đồng dạng
5. Hai tam giác cân có một góc bằng nhau thì đồng dạng
6. Nếu hai tam giác đồng dạng thì tỉ số hai đường cao tương ứng bằng tỉ số hai đường trung tuyến tương ứng
7. Hai tam đều luôn đồng dạng với nhau
II. TỰ LUẬN (7 điểm)
 Cho tam giác ABC vuông tại A có AB = 12 cm, AC = 16 cm. Vẽ đường cao AH.
	a) Chứng minh HBA ABC
	b) Tính BC, AH, BH.
	c) Vẽ đường phân giác AD của tam giác ABC (D BC). Tính BD, CD.
	d) Trên AH lấy điểm K sao cho AK = 3,6cm. Từ K kẽ đường thẳng song song BC cắt AB và AC lần lượt tại M và N. Tính diện tích tứ giác BMNC.	
C. ĐÁP ÁN VÀ BIỂU ĐIỂM
I TRẮC NGHIỆM: ( 3 điểm)
Câu
1
2
3
4
5
6
1
2
3
4
5
6
7
Đáp án
A
B
B
B
B
S
Đ
Đ
Đ
Đ
Đ
Đ
Điểm
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
II. TỰ LUẬN (7 điểm)
Câu
Đáp án
Biểu điểm
0,5
a)
Chứng minh HBA ABC
Xét HBA và ABC có:
 = = 900
 chung
=> HBA ABC (g.g)
0,25
0,25
0,25
0,25
b)
Tính BC, AH, BH
 Ta có vuông tại A (gt) BC2 = AB2 + AC2 BC = 
Hay: BC = cm
0,5
0,5
Vì vuông tại A nên: 
 = (cm)
0,5
0,5
 HBA ABC
 hay : = = 7,2 (cm)
1,0
c)
Tính BD, CD
Ta có : (cmt) hay 
 => BD = cm 
Mà: CD = BC – BD = 20 – 8,6 = 11,4 cm
0,5
 0,25
0,25
d)
Tính diện tích tứ giác BMNC.
Vì MN // BC nên AMNABC và AK,AH là hai đường ao tương ứng
Do đó: 
Mà: SABC = AB.AC = .12.16 = 96
=> SAMN = 13,5 (cm2)
Vậy: SBMNC = SABC - SAMN = 96 – 13,5 = 82,5 (cm2)
0,25
0,5
0,25
0,25
0,25
Lưu ý: Mọi cách giải khác nếu đúng và có lập luận chạc chẽ đều cho điểm tói đa câu bài đó.